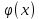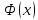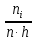Лабораторная работа по статистике. Л_Р_2 вариант. Имеется выборка объемом 20 элементов (малая выборка), равных количеству выходов из строя в сутки автобусов предприятия
 Скачать 56.45 Kb. Скачать 56.45 Kb.
|
|
Задание 1. Имеется выборка объемом 𝑛=20 элементов (малая выборка), равных количеству выходов из строя в сутки автобусов предприятия.
Требуется: 1.1. Построить вариационный ряд. 1.2. Найти 𝑥𝑚𝑖𝑛, 𝑥𝑚𝑎𝑥, 𝑧1⁄4, 𝑧3⁄4, med и построить «ящик с усами». 1.3. Построить статистический ряд и полигон. 1.4. Вычислить выборочные числовые характеристики 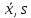 . . Решение: 1.1. Для построения вариационного ряда, упорядочим элементы выборки в неубывающем порядке: 0, 1, 2, 3, 3, 3, 4, 4, 4, 4, 5, 5, 5, 5, 6, 6, 7, 7, 8, 9. 1.2. Найдем 𝑥𝑚𝑖𝑛, 𝑥𝑚𝑎𝑥, 𝑧1⁄4, 𝑧3⁄4, med. 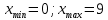 Выборочные квартили 𝑧1⁄4 , 𝑧3⁄4 это элементы вариационного ряда, на четверть отстоящие от краев. Их точное определение дается формулами: 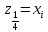 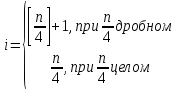 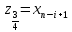 При 𝑛=20 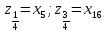 . Значит, . Значит,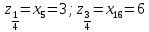 . .Выборочные квартили 𝑧1⁄4, 𝑧3⁄4 являются статическими оценками соответствующих генеральных квартилей 𝑥1⁄4 и 𝑥3⁄4 , определяемых как корни уравнений 𝐹(𝑥)=1⁄4 и 𝐹(𝑥)=3⁄4, где 𝐹(𝑥) – непрерывная строго возрастающая генеральная функция распределения. Медиана выборки 𝑚𝑒𝑑 это средний элемент вариационного ряда, если объем выборки 𝑛 – число нечетное, или полусумма двух средних элементов, если 𝑛 – четное. Значит 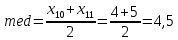 Ящик с усами дает сжатое обобщенное представление о выборке. 𝑥𝑚𝑖𝑛 𝑧1⁄4 med 𝑧3⁄4 𝑥𝑚𝑎𝑥   0 3 4,5 6 9 1.3. Построим статистический ряд и полигон.
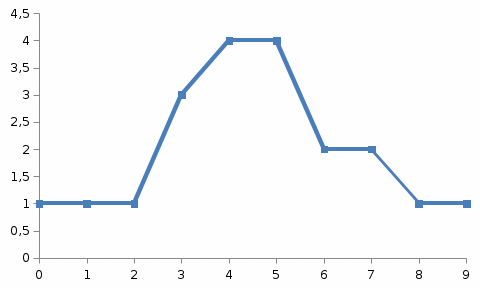 1.4. Вычислим выборочные числовые характеристики 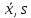 . .выборочную среднюю 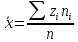 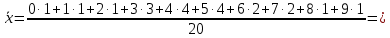 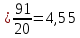 выборочную дисперсию 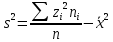 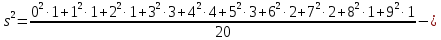 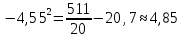 среднее квадратическое отклонение 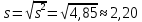 Задание 2. Дана большая выборка, объемом 100 элементов, которые могут интерпретироваться как отклонения результатов измерения изучаемой случайной величины 𝛸 от ее среднего значения. Данные выборки являются фрагментами таблицы случайных чисел, распределённых нормально 𝑁(0; 1).
Требуется: 2.1. Построить группированный статистический ряд. 2.2. Построить гистограмму приведенных частот 𝑛𝑖⁄(𝑛ℎ) (𝑛𝑖 – частоты попадания элементов выборки в промежутки, 𝑛 – объем выборки, ℎ – длина каждого промежутка). 2.3. Построить полигон приведенных частот 𝑛𝑖⁄(𝑛ℎ) для средних точек 𝑧𝑖 промежутков группированного статистического ряда. 2.4. Построить эмпирическую функцию распределения 𝐹∗(𝑥) и её график – кумуляту для средних точек 𝑧𝑖 промежутков группированного статистического ряда. 2.5 .Относительную частоту 𝑝𝑏∗ события 𝑋 0. 2.6. Для сравнения вместе с гистограммой в том же масштабе построить стандартная нормальная кривая 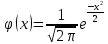 . Значения функции (𝑥) (Гаусса) приведены в таблице 1.1. . Значения функции (𝑥) (Гаусса) приведены в таблице 1.1.Таблица 1.1. Значения функции Гаусса (x).
2.7. Для сравнения вместе с кумулятой в том же масштабе построить график функции Лапласа 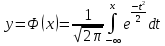 Ее значения приведены в таблице 1.2 Таблица 1.2. Значения функции Лапласа (x).
2.8. Вычислить 𝑥 и 𝑠 – оценки генерального математического ожидания 𝑚x и среднего квадратического отклонения 𝜎x, соответственно. 2.9. Вычислить точность 𝜀 оценки 𝑥 при заданной надежности 𝛾 = 0.95 . 2.10. Построить доверительный интервал для математического ожидания 𝑚 нормальной генеральной совокупности при 𝛾 = 0.95. Решение: Образуем группированный статистический ряд. Найдем xmin, xmax. xmin=−2,1; xmax=2,5. Вычислим размах 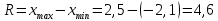 Число промежутков группированного статистического ряда примем равным 𝑘=8. Длина каждого промежутка 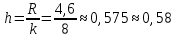 Образуем промежутки группированного статистического ряда: 1=[ -2,1; -1,52) 2=[ -1,52; -0,94) 3=[ -0,94; -0,36) 4=[ -0,36; 0,22) 5=[0,22; 0,80) 6=[0,80; 1,38) 7=[1,38; 1,96) 8=[1,96; 2,54). Распределим элементы выборки по образованным промежуткам i и подсчитаем частоты в каждом промежутке ni(i = 1, , 8).
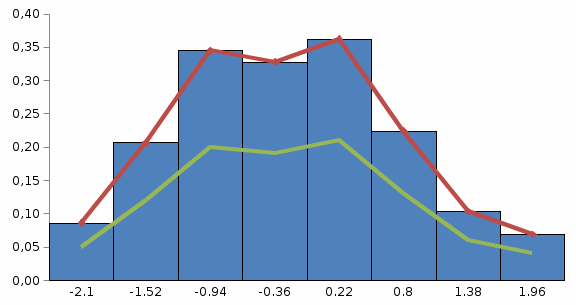 Найдем эмпирическую функцию распределения: 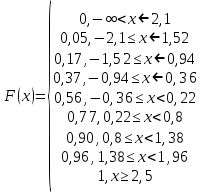 Построим график полученной функции: 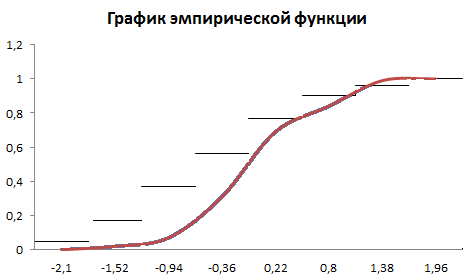 Вычислим числовые характеристики 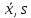 . .выборочную среднюю 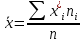 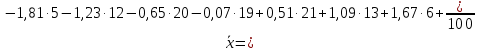 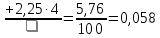 выборочную дисперсию 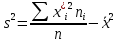 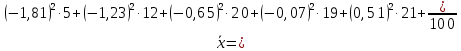 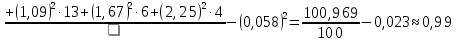 Среднее квадратическое отклонение равно 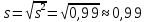 Вычислим относительную частоту события X 0: 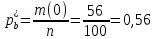 Вычислим точность 𝜀 оценки 𝑥 при заданной надежности 𝛾=0.95. Для чего применим формулу 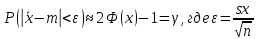 Тогда, 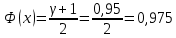 . . C помощью таблицы квантилей нормального распределения 𝑁(0; 1) находим квантиль 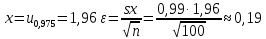 Итак, точность оценки равна 0,19 и величина 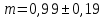 c надежностью 𝛾=0,95. c надежностью 𝛾=0,95.Построим доверительный интервал для 𝑚 при 𝛾=0.95: 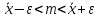 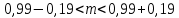 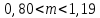 | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||