Проверка гипотезы о значение двух средних из нормально распределенных генеральных совокупностей.. 28. Проверка гипотезы о значение двух средних из нормально распределенных генеральных совокупностей
 Скачать 110.05 Kb.
|
|
28. Проверка гипотезы о значение двух средних из нормально распределенных генеральных совокупностей. Здесь рассматривается случай независимых выборок. На практике часто возникает необходимость сравнить, например, свойства материалов из двух партий (двух плавок, термообработок, двух методов измерений и т.п.). Пусть получены статистические характеристики  где цифры 1, 2 относятся к номерам партий. Проверка гипотезы о равенстве двух средних производится следующим образом.1. Выдвигается гипотеза  2. Выбирается уровень значимости . 3. Критической статистикой служит следующая функция выборочных данных. 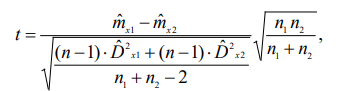 где n1 и n2 соответственно количество экспериментальных точек в первой и во второй партиях. 4. Критическое значение статистики  ищется по таблице Стьюдента с n1 n2 2 , степенями свободы для уровня значимости . 5. Рассчитанное значение t сравнивается с критическим t . При  t гипотеза H0 отвергается, при  гипотеза H0 принимается. В последнем случае говорят, что среднее значение выборок значимо не отличается в статическом смысле.Если объем независимых выборок одинаково, то есть n1 n2 n , то формула упрощается 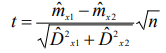 27. Проверка гипотезы о равенстве двух дисперсий из нормально распределенных генеральных совокупностей. Прежде, чем сравнивать между собой две выборки (например, на равенство средних), необходимо убедиться, что дисперсия этих двух выборок равны между собой (не отличаются) в статистическом смысле. Такая проверка делается с помощью критерия Фишера. Выдвигается гипотеза  Выбирается уровень значимости . Критической статистикой служит следующая функция. 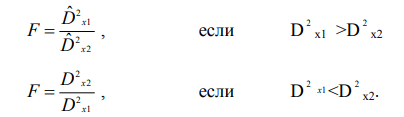 Критическое значение статики F соответствует распределению Фишера с  степенями свободы. Таблица распределения Фишера приведена в приложении E, где сверху указаны степени свободы большей дисперсии, ( 1 ), а слева – степени свободы меньшей дисперсии ( 2 ). 26. Проверка гипотезы о законе распределения по методу К. Пирсона. В этом методе мерой расхождения теоретического и статистического законов распределения служит сумма квадратов разностей между частотой и вероятностью попадания случайной величины в интервале, на которые разбиваются множество возможных значений этой величине. Проверка гипотезы применительно к нормальному закону распределения осуществляется следующим образом 1. Выдвигается гипотеза H0, что статистический закон подчиняется нормальному закону распределения. 2. Выбирается уровень значимости . 3. Наблюдаемые значения случайной величины разбиваются наl интервалов и вычисляют показатель согласованности по следующей формуле 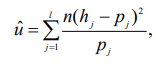 где hj частота, pj – вероятность попадания случайной величины в j-й интервал, или по следующей формуле, которая получается из формулы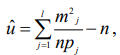 где mj – число наблюдений, попавших в j-й интервал.Вероятность Pj попадания случайной величины X, следующей гипотетическому закону распределения, в j-й разряд (интервал) вычисляется следующим образом 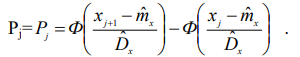 , где F x ˆ – теоретический закон распределения с параметрами (mx и Dx), получения из эксперимента. Для нормального закона распределения формулу можно переписать так: 4. Критическая граница  для нормального закона распределения ищется по таблице  (распределение Пирсона) с (l-3) степенями свободы. То есть для нормального закона распределения  Распределение приведено в лабораторной работе по надежности «Доверительные интервалы». 5. Проверяется условие u . Если оно выполняется, то расхождение между экспериментальными данными и гипотезой полагают несущественным. В противном случае гипотезы H0 отвергается.25. Проверка о законе распределения по методу Н,В, Смирнова При выборке по методу Н.В. Смирнова в качестве меры согласования теоретического и статического законов распределения используются функция разности статической и теоретической функции распределения. Проверка гипотезы осуществляется следующим образом. 1. По внешнему виду (на графике) функции распределения выдвигается нулевая гипотеза, что распределение подчиняется закону F(x) (например, нормальному). 2. Назначается уровень значимости . 3. Вычисляется наблюдаемое значение критической статистики (показателя согласованности по формуле 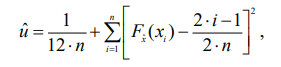 где n – количество экспериментальных точек; Fx(xi) – теоретическое значение исследуемой функции распределения при параметрах распределения (mx и Dx), найденных из эксперимента; i – порядковый номер наблюдения в упорядоченной по возрастанию выборке. Если проверяется нормальный закон распределения, то вместо функции Fx(xi) берется табличное значение нормированной нормальной функции распределения, то есть. 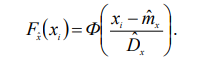 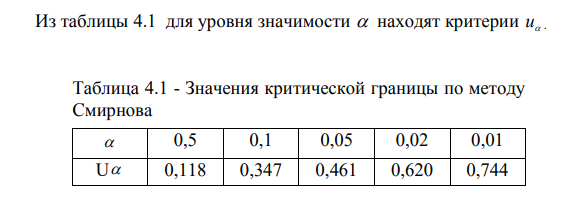 4. Проверяется условие u u . Если оно выполняется, то нулевая гипотеза принимается. Этот метод применяется, если выборка представлена отдельными экспериментальными точками. 24. Статистическая проверка гипотез при оценке резко выделяющихся членов выборки Покажем методику проверки одним из наиболее простых методов с помощью так называемого r – критерия 1. Выдвигается гипотеза:  принадлежит данной выборке, а его отличие от остальных членов выборки – случайно. 2. Назначается уровень значимости . 3. Вычисляются следующие статистические характеристики:  где mx –оценка математического ожидания; Dx – оценка среднего квадратичного отклонения; n –количество экспериментальных данных.4. Критическое значение  выбирают по таблице, приведенной в приложении Д для заданного уровня значимости и числа степеней свободы =n-2. 5. Если окажется, что  то гипотеза отвергается и следует отбросить данное экспериментальное значение выборки.23. |