Построение организационной структуры. Метод анализа иерархий. Тема метод анализа иерархий (маи)
 Скачать 240 Kb.
|
|
Тема 1. МЕТОД АНАЛИЗА ИЕРАРХИЙ (МАИ) Этот метод выбора альтернатив при принятии решения достаточно широко применяется при решении разных практических задач: Он основан на экспертных оценках. Центральным вопросом, который решается МАИ является вопрос: насколько значительно влияние самого нижнего уровня иерархии (обычно это альтернативы) на вершину (главную цель системы). Цель МАИ – дать количественную характеристику этого влияния, т.е. установить приоритеты элементов нижнего уровня относительно одного элемента высшего уровня. В МАИ используется 3 метода сравнения альтернатив: попарное сравнение; сравнение альтернатив относительно стандартов и сравнение альтернатив копированием. Мы рассмотрим попарное сравнение. 1. Построение иерархий При решении сложной проблемы, ее часто разбивают на отдельные элементы ,которые объединяются в группы в соответствии с распределением некоторых свойств между ними. Группы рассматриваются в качестве элементов уровня системы. Эти элементы, в свою очередь, могут быть сгруппированы в соответствии с другим набором свойств, создавая элементы еще более высокого уровня, пока не будет достигнут единственный элемент - который обычно отождествляется с целью принятия решения. Обычно все это называют иерархией. Иерархия - это тип системы , основанной на предположении, что элементы системы могут группироваться в несвязанные множества. Элементы каждой группы находятся под влиянием некоторой вполне определенной группы и в свою очередь оказывает влияние на элементы другой группы. Считаем, что элементы в каждой группе иерархии (называемой уровнем, кластером, стратой) независимы. Случай наличие зависимости должен рассматриваться отдельно. Могут быть различные типы иерархий по связям элементов нижнего и верхнего уровня. Мы будем считать, что каждый элемент верхнего уровня связан со всеми элементами нижнего уровня. Типичная иерархия для решения многих задач может быть представлена следующей схемой  Рис. 1. Типичная иерархия. Итак, следует помнить, что основные цели устанавливаются на вершине иерархии; их подцели - непосредственно ниже вершины, силы ограничивающие акторов - еще ниже. Силы доминируют под уровнем самих акторов, которые в свою очередь доминируют под уровнем своих целей, ниже которых будет уровень их возможных действий и в самом низу находится уровень различных возможных исходов (сценариев). Это естественная форма, которую принимают иерархии связана с планированием и конфликтами. Определение приоритетов факторов низшего уровня относительно цели может быть сведена к последовательности задач определения приоритета для каждого уровня, а каждая такая задача - к последовательности парных сравнений. Сравнение – основная составляющая теории МАИ, даже если исходная задача осложняется, условиями обратной связи между разными уровнями или факторами. Пример. Определить сценарий (программу), согласно которому с наибольшей вероятностью будет обеспечено продолжительное существования колледжа. Назовем благосостояние колледжа общей целью. На нее влияют следующие силы : обучение, общественная жизнь, дух(атмосфера), наличие оборудования и внешкольная деятельность. Эти силы определяются следующими действующими лицами (акторами): академической администрацией, неакадемической администрацией, профессорско - преподавательским составом, студентами, попечителями. Мы опускаем очевидную обратную связь между силами и акторами. Различные акторы имеют определенные цели: профессорско - преподавательский состав может хотеть сохранить свою работу, расти профессионально, качественно проводить обучение; студенты могут быть заинтересованы в получении работы, в женитьбе, в получении хорошего образования т.д. Наконец имеется несколько возможных сценариев, таких как : статус-кво, акцент на профессиональное обучение, дальнейшее образование или превращение в религиозную школу. Сценарии определяет вероятность достижения целей, цели влияют на акторов, акторы направляют силы, которые воздействуют на благосостояние последних. Таким образом , мы получаем иерархию. Как уже было отмечено, нас интересует сценарий по которому с наибольшей вероятностью будет обеспечено продолжительное существование колледжа. Для определения этого сценария сначала находим важность сил относительно общей цели. Затем для каждой силы определяется степень влияния акторов на эту силу. Отсюда несложными вычислениями получаем степень влияния акторов на общую цель. Затем оцениваем важность целей для каждого актора и, наконец, определяем действенность различных сценариев в обеспечении достижения целей. Повторив несколько раз упомянутые выше вычисления, получим "наилучший" сценарий. Итак, определим степень влияния или приоритеты элементов одного уровня относительно их важности для элемента следующего уровня. 2. Метод парных сравнений Метод можно описать следующим образом. Допустим, заданы элементы одного, скажем 4-го уровня иерархии – A,B,C,D и один элемент E следующего более высокого уровня (3-его). Нужно сравнить элементы 4-го уровня попарно по силе их влияния на E, поместить числа, отражающие достигнутое при сравнении согласия во мнениях, в матрицу (матрицу парных сравнений) и найти собственный вектор с наибольшим собственным значением. Собственный вектор обеспечивает упорядочение приоритетов, а собственное значения является мерой согласованности суждений. Покажем, как определяется шкала приоритетов на следующем простом примере. Пусть А, В, С и D обозначают стулья, расставленные по прямой линии, ведущей от источника света. Создадим шкалу приоритетов относительной освещенности для стульев. Суждение производит человек, сидящий около источника света, у которого например спрашивают : "насколько сильнее освещенность стула В по сравнению с С. " Он отвечает одним из чисел и это суждение им заносится в позицию (В,С) в матрице. По соглашению сравнения всегда производятся для действия или объекта, стоящих в левом столбце (заголовки строк), по отношению к действию или объекту, стоящему в верхней строке (заголовки столбцов). Мы имеем матрицу непарных сравнений для четырех строк и четырех столбцов (4х4).
Условимся, что числа в матрице определяются следующим образом: А и В одинаково важны, заносим 1 в позицию (А,В). А незначительно важнее, чем В, заносим 3. А значительно важнее В, заносим 5. А явно важнее В, заносим 7. А по своей значительности абсолютно превосходит В, заносим 9. Так как при сравнении элемента с самим собой имеем равную значительность, таким образом, на главной диагонали должны стоять единицы. Если в позиции (А,В) мы записали число d, то в позиции (В,А) должно стоять число 1/d. Эта градация общепринята, большинство людей различают при сравнении эти пять позиций. Если наши ощущения сильно отличаются от суждений (1-5), то заносим числа 2,4,6,8 и т.п. Полученную матрицу необходимо проверить на согласованность суждений. В общем случае под согласованием подразумевается то, что при наличии некоторого числа суждений (основных), все другие данные логически могут бать получены из них. Для проведения парных сравнений n объектов, при условии, что каждый объект представлен в данных, по крайней мере, один раз, требуется (n-1) суждений о парных сравнениях. Из них можно просто вывести все остальные суждения, используя следующие отношения : если объект А1 в 5 раза превосходит объект B и в 6 раз превосходит C, то А1=5B и А1=6C. Следовательно, 5B=6C или B=  C и C= B. Если численное значение суждения в позиции (B,C) не равно , то матрица будет несогласованной . Это случается часто и не является бедствием. Для большинства задач очень трудно определить (n-1) суждений связывающих все объекты или виды действия, одно из которых является абсолютно верным.Известно, что согласованность положительной обратносимметричной матрицы эквивалентно требованию  max= n, где max - максимальное собственное значение матрицы. Насколько плоха согласованность для конкретной задачи можно оценить путем сравнения значения величины ( max - n)/(n-1) с ее значением из случайно выбранных суждений и соответствующих обратных величин матрицы того же разряда. Подробнее согласование рассмотрим ниже.В нашей матрице мы произвели 6 сравнений. Теперь необходимо вычислить вектор приоритетов по данной матрице. То есть вычислить главный собственный вектор, который после нормализации становится вектором приоритетов. Так как данные в нашей матрице весьма приближенные, можно получить грубые оценки этого вектора следующими 4-мя способами, которые расположены в порядке увеличения точности: Суммировать элементы каждой строки и нормировать делением каждой суммы на сумму всех элементов, (сумма полученных результатов = 1). Первый элемент результирующего вектора будет приоритетом первого объекта, 2-ой - 2-ого и т.д. Суммировать элементы каждого столбца и получить обратные величины этих сумм. Нормировать их так, чтобы их сумма равнялась единице (разделить каждую обратную величину на сумму всех обратных величин ). Разделить элементы каждого столбца на сумму элементов этого столбца (то есть нормировать столбец), затем сложить элементы каждой полученной строки и разделить эту сумму на число элементов строки Это - процесс нормированности столбца. Умножить n элементов каждой строки и извлечь корень n-степени, нормировать полученные числа. Если матрица согласована, то методы 1-4 дают один и тот же результат. В общем случае, когда матрица не согласованна эти методы дают различные результаты. В примере со стульями по - 1-му методу 0,51 0,3 0,15 0,04 - 2-му методу 0,68 0,16 0,09 0,06 - 3-му методу 0,59 0,245 0,115 0,05 - 4-му методу 0,61 0,24 0,1 0,04 Точное решение задачи (методами матричной алгебры): 0,61 0,24 0,1 0,05 3. Метод получения грубой оценки согласованности Этот метод состоит в следующем: Умножив матрицу сравнений справа на полученную оценку вектора решения, получим новый вектор. Разделив первую компоненту этого вектора на первую компоненту оценки вектора решения, вторую на вторую и т.д., определим еще один вектор. Разделив сумму компонент этого вектора на число компонент найдем приближение для max . Чем ближе max к n (числу объектов или видов действия в матрице), тем более согласован результат. Отклонение от согласованности может быть выражено величиной ( max - n)/(n-1) , которую назовем индексом согласованности (ИС).Вводится еще одна величина – ИС/СИ ,где СИ - случайный индекс сгенерированный по шкале от 1 до 3 обратносимметричной матрицы (имеются соответствующие таблицы). Таблица 1
Отношение ИС/СИ называется отношением согласованности (ОС). Значение ОС меньше или равное 0,1 будем считать приемлемым. Используя приведенную схему расчета , получим для нашей матрицы ИС=0,13. СИ для нашей матрицы - 0,9. Получим ОС = 0,14, что не слишком хорошо. Эти сравнения и вычисления устанавливают приоритеты элементов некоторого уровня иерархии относительно одного элемента следующего уровня. Если уровней больше, чем два, то различные векторы приоритетов могут быть объединены в матрицы приоритетов, из которых определяется один окончательный вектор приоритетов для нижнего уровня. 4. Пример иерархической композиции приоритетов. Задача о выборе школы. Был проведен анализ трех школ A, B и С на предмет их желательности с точки зрения молодого человека. Для сравнения были выбраны шесть независимых характеристик: учеба, друзья, школьная жизнь, профессиональное обучение, подготовка к колледжу и обучение музыке. Удовлетворение школой Общая цель У Д Ш П К М Силы ау ад аш ск см ап сп ак вд вш вп вк сд сш ам ву вм су Сценарий А В С Рис.2. Иерархия удовлетворения школойДля решения поставленной задачи необходимо выполнить следующие пункты: определить важность сил относительно общей цели определить действенность каждого сценария относительно сил определить приоритеты (т.е. действенность каждого сценария относительно цели). Рассмотрим подробное решение поставленной задачи 1. Сравнение характеристик относительно общего удовлетворения школой (шкала 9 баллов) Таблица 2.
   Вектор приоритетов  У Д Ш П К М2. Таблицы 3-8
Итоговая таблица приоритетов школ для сил. Таблица 9.
Общая оценка школы относительно целей Для получения общей оценки каждой школы нужно умножить все оценки этой школы по некоторому критерию на вес этого критерия. Затем следует сложить значения, полученные для каждой школы, по всем критериям. Математически - надо матрицу таблицы 17 умножить на вектор приоритетов таблицы 1, т.е.  - вектор приоритетов школ относительно цели – «большей удовлетворенности школой».Была выбрана школа А, т.к. она получила почти такую же оценку, что и школа В и была бесплатной, а школа В была частной, за обучение в ней надо было платить 1600$ в год. Следует заметить однако, что решение было принято при значительной несовместимости суждений на уровне 2 (таблица 1), что могло привести к плачевному результату, но к счастью не привело. Через 3 года оценка была проведена вновь и были получены следующие приоритеты:  .5. Оценка однородности иерархий Рис. 3. Пример иерархии для оценки согласованности. П  усть задана иерархия критериев и альтернатив ИО1- индекс однородности ( согласованности ) 1-ого уровня; {ИО2, ИО3}- вектор индексов однородности 2-ого уровня; { ИО4, ИО5, ИО6}- вектор индексов однородности 3-его уровня; W1- вектор приоритетов критериев K2 и K3 относительно K1; {W2},{W3}- векторы приоритетов критериев K4, K5, K6 относительно K2 и K3 В этом случае ИОИ ,СИИ и ООИ можно определить по формулам: 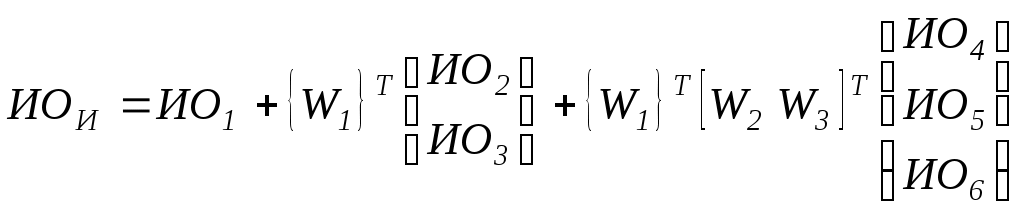   Однородность иерархии считается удовлетворительной при ООИ<0.1 6. Учет мнений нескольких экспертов Для агрегирования мнений экспертов принимается среднегеометрическое, вычисляемое по следующему соотношению  здесь -  агрегированная оценка элемента, принадлежащая i-ой строке и j-ому столбцу матрицы парных сравнений; n – число матриц парных сравнений, каждая из которых составлена одним экспертом.Осреднение суждений экспертов может быть осуществлено и на уровне собственных векторов матриц парных сравнений. При этом результаты будут эквивалентны тем, которые получены после осреднения матрицы, если ОО<0.1 для матрицы. В достаточно ответственных задачах, осреднение суждений экспертов производится с «весом». Сначала по следующей иерархии определяется их «вес» (приоритет).  Рис. 4. Иерархия для нахождения «веса» экспертов. Далее по формуле  ,где  - оценка объекта, приведенная k-ым экспертом с весовым коэффициентом  при этом  ;определяют агрегированную матрицу попарных сравнений. 7. Выводы по МАИ Подход к парным сравнениям, основанный на решении задачи о собственном значении, обеспечивает способ шкалирования, особенно в тех сферах, где не существует измерений и количественных сравнений. Мера согласованности позволяет возвратиться к суждениям, уточняя их для улучшения общей согласованности. Участие нескольких человек позволяет приходить к компромиссам между различными элементами, а также может вызвать диалог о том, каким следует быть действительному отношению - компромиссу между различными суждениями, представляющими разный опыт. Этапы процесса проходят следующим образом: Сформулируйте задачу. Поставьте задачу в общем плане - вставьте ее (если есть необходимость) в большую систему, включающую другие действующие лица, их цели и результаты. Идентифицируйте критерии, влияющие на задачу. Постройте иерархию общих критериев, частных критериев, свойств альтернатив и самих альтернатив. В задаче со многими участниками уровни могут относиться к окружающей среде, акторам, их целям, политике и результатам, из которых получаем обобщенный результат (состояние сферы действия). Чтобы устранить неясность, тщательно определите каждый элемент в иерархии. Установите приоритеты первичных критериев относительно их воздействия на общую цель, называемую фокусом. Ясно сформулируйте вопрос для парных сравнений в каждой матрице. Обратите внимание на ориентацию каждого вопроса, например, стоимость должна уменьшаться, а эффективность увеличиваться. При проведении попарных сравнений целей (критериев) обычно спрашивают, какая из них более важна, а при сравнении альтернатив (сценариев) – какая более предпочтительна или вероятна. Установите приоритеты частных критериев относительно своих общих критериев. Введите суждения о попарных сравнениях и их обратные величины. Вычислите приоритеты путем, например, суммирования элементов каждого столбца и деления каждого элемента на общую сумму столбца. Усредните по строкам результирующую матрицу, и вы получите вектор приоритетов. В случае сценариев прокалибруйте их переменные состояния по шкале от -8 до +8 в зависимости от того, насколько они отличаются от существующего состояния, обозначаемого 0. Составьте веса в иерархии для получения общих приоритетов, а также составных значений переменных состояния, которые вместе определяют общий результат. В случае выбора среди альтернатив выберите альтернативу с небольшим приоритетом. В случае размещения ресурсов оцените стоимость альтернативы, вычислите отношение эффективности к стоимости и распределите ресурсы соответствующим образом: или полностью, или пропорционально. В задаче определения приоритетов стоимости распределите ресурсы пропорционально приоритетам. Задача Правительственное агентство должно решить строить или не строить туннель и/или мост через реку, которую в настоящее время обслуживает паром. Выгоды: экономическая (В1): время (С1); доход (С2); торговля (С3) вдоль реки; работа по строительству (С5); торговля в окрестностях (С4). Социальные (В2): безопасность и надежность (С6); гордость общины (С8); связи (С7). Окружающая среда (В3): комфорт (С9); доступность (С10); эстетика (С11). Сценарии: D1 – мост D2 – туннель D3 – существующий паром Издержки: Экономические  :капиталовложения  ;эксплуатация и текущий ремонт  ;прекращение паромного бизнеса  .Социальные  изменение стиля жизни  ;раскол людей  ;передислокация людей  .Окружающей среды  :повышение загазованности от автомобилей  ;разрушение экологии  ;загрязнение воды из-за моста  . – мост; – туннель; – существующий паром.Указание: в анализе использовать критерий: найти максимум по i отношения  для i=1..3Что делать – строить мост или туннель или не строить? | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
