Двухканальная система массового обслуживания. имитационное моделирование систем массового обслуживания по дисциплине Моделирование процессов и систем

• Название: имитационное моделирование систем массового обслуживания по дисциплине Моделирование процессов и систем
• Анкор: Двухканальная система массового обслуживания
• Дата: 21.11.2022
• Размер: 372.54 Kb.
• Имя файла: Otchet_2_Vakhitov.docx
• Тип: Документы; #803772

МИНИСТЕРСТВО ЦИФРОВОГО РАЗВИТИЯ СВЯЗИ И МАССОВЫХ КОММУНИКАЦИЙ РОССИЙСКОЙ ФЕДЕРАЦИИ

ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ БЮДЖЕТНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ

«САНКТ-ПЕТЕРБУРГСКИЙ ГОСУДАРСТВЕННЫЙ УНИВЕРСИТЕТ ТЕЛЕКОММУНИКАЦИЙ ИМ. ПРОФ. М.А. БОНЧ-БРУЕВИЧА»

(СПбГУТ)

ОТЧЁТ

по лабораторной работе №2 на тему:

«ИМИТАЦИОННОЕ МОДЕЛИРОВАНИЕ СИСТЕМ МАССОВОГО ОБСЛУЖИВАНИЯ»

по дисциплине «Моделирование процессов и систем»


Выполнил: студент группы ИСТ-032, Вахитов А.А.

«___» ________ 2022г. __________/А.А. Вахитов

Принял: к. т. н. доцент ИУС, Козлова Л.П.

«___» ________ 2022 г. ________/Л. П. Козлова/

Санкт-Петербург

2021

Цель работы

Разработать модель системы массового обслуживания на примере банка.
Задание 1

Выполните имитацию работы банка, осуществляющего прием вкладов. Размер депозита является случайной величиной с нормальным законом распределения (среднее значение -MD ; среднее квадратическое отклонение - SD ). Время между приходом двух вкладчиков – случайная величина с показательным законом распределения (среднее значение - tz ), а время обслуживания равномерно распределено на интервале [ a ; b ].

Пусть исходные значения равны величинам: MD =30000 руб.; SD =10000 руб.; tz =1 час; a =20 мин.; b =30 мин.; tn =9 ч., число заявок равно 5.

Определите время прихода последнего клиента, среднее время пребывания клиента в системе. Какой общий размер вкладов будет осуществлена) после прихода пяти клиентов; б) к моменту времени 12:00 ч.?

Задание 2

Проведите 10 экспериментов и рассчитайте величины:

- среднее время ожидания;

- среднее число обслуженных заявок за период с 9:00 до 15:00 ч.

Задание 3

Предположите, что tn = 0 и выполните имитацию описанным на рис. 1.3 способом.

Задание 4

Пусть банковская автоматизированная система может выходить из строя, что приводит к необходимости вызова специалистов, устраняющих неполадку. Выполните имитацию периодов нормальной работы системы и ее ремонта, если данные величины являются случайными с показательным законом распределения, а tz =30 дней, to =3 ч. Рассмотрите процесс поступления 5 заявок (отказов).
Ход работы

Задание 1

1. 
   Формируем таблицу исходя из начальных значений в задании. Начальные значения выделены синим цветом и находяться в ячейках: F2, F3, I2, I3, D7.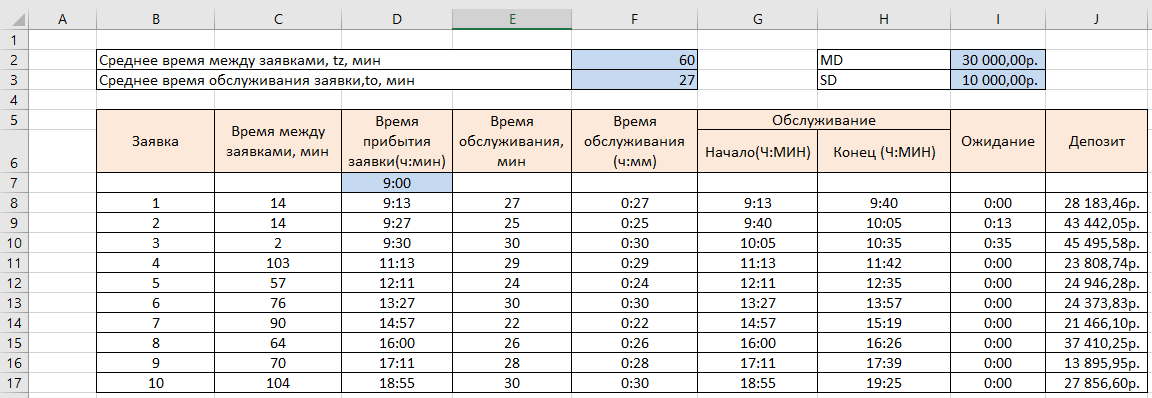
   

2. 
   Размер депозита сформирован с помощью формулы:
   

3. 
   Время между приходом двух вкладчиков сформировано с помощью формулы:
   

4. 
   Основываясь на полученных значениях в столбце «Время между заявками», рассчитывается для каждой заявки время ее прибытия
   

5. 
   С помощью функций Excel формируются случайные значения для столбца «Время обслуживания»
   

6. 
   Столбец «Время обслуживания (ч:мм)»
   

7. 
   Для каждой заявки рассчитывается время начала ее обслуживания
   

8. 
   И время окончания обслуживания заявки
   

9. 
   Находится время ожидания для каждой заявки
   

Теперь определяем время прихода последнего клиента, среднее время пребывания клиента в системе, общий размер вкладов после прихода пяти клиентов, общий размер вкладов к моменту времени 12:00 ч.

Получаем такую таблицу:



в котором:

1. 
   Время прихода последнего клиента:
   
   
2. 
   Среднее пребывание клиента в системе, мин:
   
3. 
   Общий размер вкладов после прихода 5 клиентов:
   

4. 
   Общий размер вкладов к моменту времени 12ч:
   

Можно сформировать такого рода диаграмму «Ожидание - Время обслуживания»: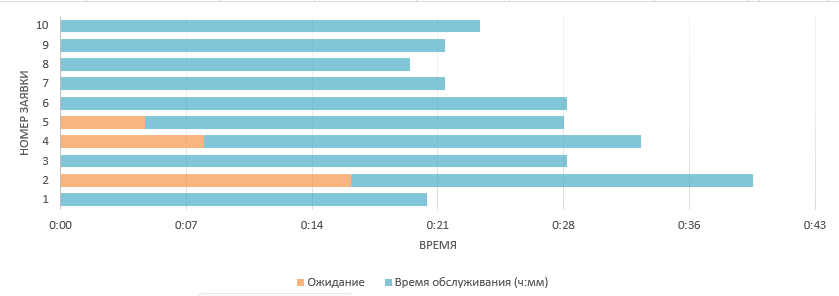


Задание 2

Проводим 10 экспериментов: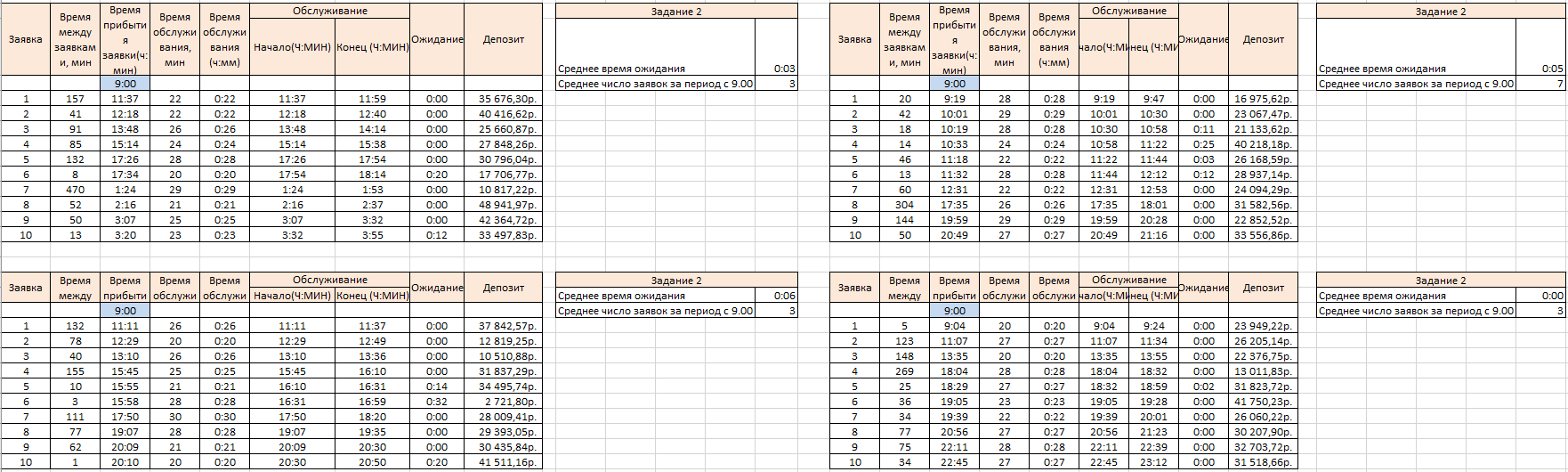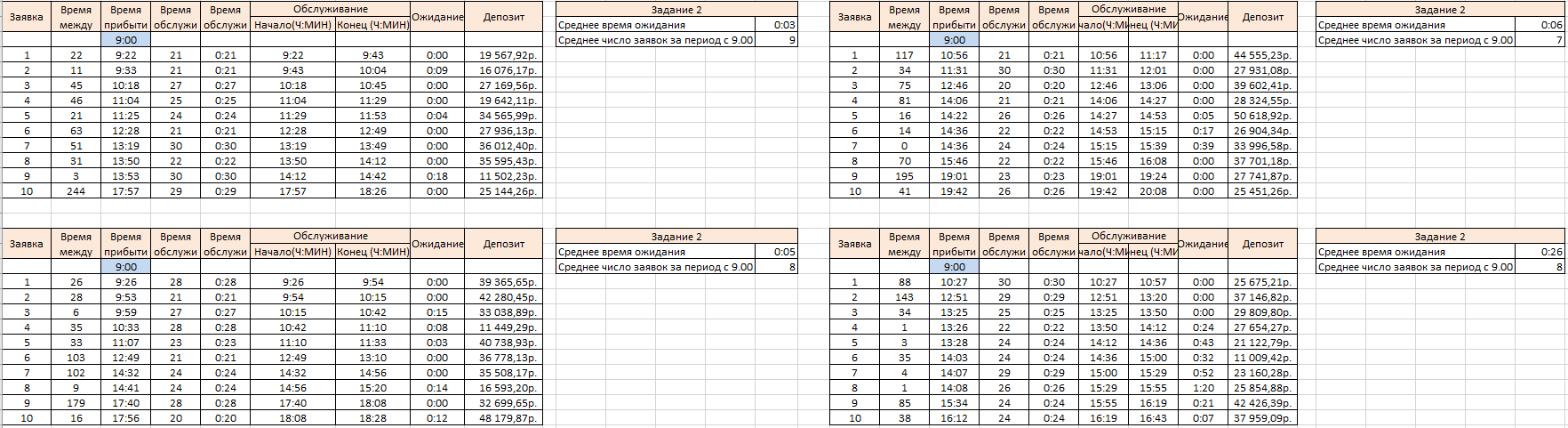







На основании этих экспериментов проводим расчет

1. 
   Среднее время ожидания
   
   
2. 
   Среднее число заявок за период с 9:00 до 15:00 ч.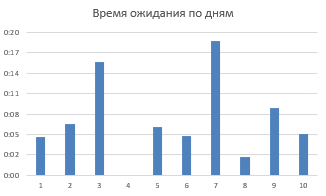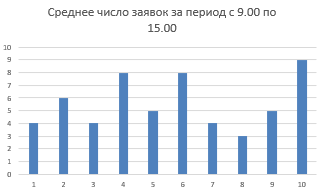
   
   

Задание 3

Основываясь на начальных данных, создаем таблицу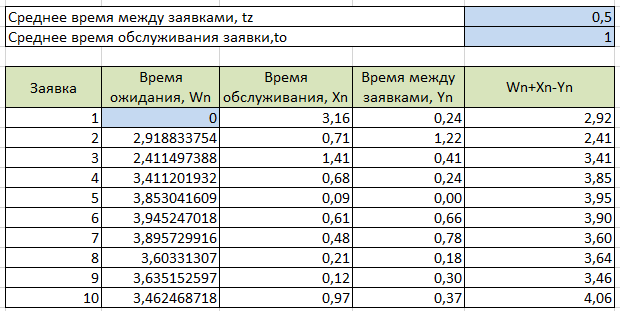



Формулы для расчета таблицы:

1. 
   Время ожидания
   
   
2. 
   Время обслуживания
   
   
3. 
   Время между заявками
   
   
4. 
   Wn+Xn-Yn
   
   

Диаграмма «Время ожидания – Время обслуживания»: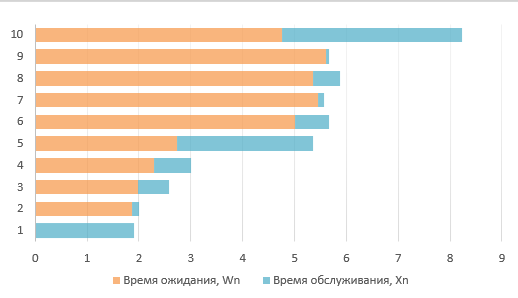



Задание 4

Для выполнения имитации периодов нормальной работы системы и ее ремонта, к таблице представленной в Задании 1 добавляются еще и столбцы «Нормальная работа» и «Ремонт»



Формулы для вычисления полей:

1. 
   Нормальная работа, дн.
   
   
2. 
   Ремонт, дн.
   
   

Диаграмма «Нормальная работа - Ремонт»: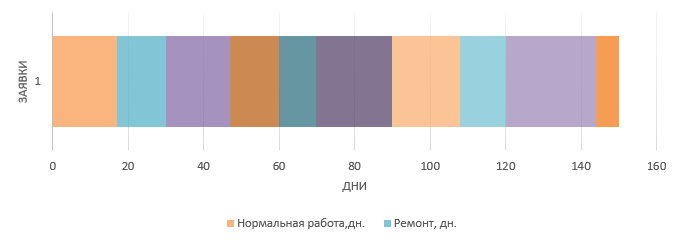



Вывод: была разработана простейшая модель системы массового обслуживания для банка.