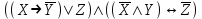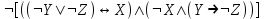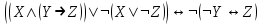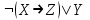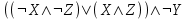16. С помощью матрицы смежности определить количество путей длины 2,3,4 из V1 в V4, из V2 в V5, определить для всех вершин графа полустепени исхода и захода, выяснить имеются ли контуры в графе. Построить реализации графов.
1 . .  2. 2.   3. 4. 3. 4.
5   . 6. 7. 8. . 6. 7. 8.
9.   10. 10.
17. Даны графы G1 и G2 . Найдите G1ÈG2, G1∩ G2, G1ÅG2 аналитически и изобразить результат графически. Для графа G1ÈG2 найдите матрицу смежности, матрицу инцидентности, компоненты сильной связности, маршруты (но не цепи) длины 7; простые цепи, простые циклы, исходящие из вершины 1.
№
|
G1
|
G2
|
№
|
G1
|
G2
|
1
|
1 2

4 3
|
1

3 2
|
16
|
1 2

4 3
|
1

3 2
|
2
|
1 2

4 3
|
1
3 2 2
|
17
|
1 2

4 3
|
1
3 2
|
3
|
1 2

4 3
|
1
3 2
|
18
|
1 2

4 3
|
1

3 2
|
4
|
1 2
4 3
|
1
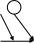
3 2
|
19
|
1 2

4 3
|
1

3 2
|
5
|
1 2

4 3
|
1

3 2
|
20
|
1 2

4 3
|
1

3 2
|
6
|
1 2

4 3
|
1
 3 2 3 2
|
21
|
1 2

4 3
|
1

3 2
|
7
|
1 2

4 3
|
1

3 2
|
22
|
1 2

4 3
|
1
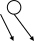
3 2
|
8
|
1 2

4 3
|
1

3 2
|
23
|
1 2

4 3
|
1
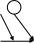
3 2
|
9
|
1 2

4 3
|
1

3 2
|
24
|
1 2

4 3
|
1

3 2
|
10
|
1 2

3 4
|
1
 
3 2
|
25
|
1 2

4 3
|
1

3 2
|
11
|
1 2
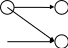
4 3
|
1

3 2
|
26
|
1 2

4 3
|
1

3 2
|
12
|
1 2
4 3
|
1

3 2
|
27
|
1 2

4 3
|
1

3 2
|
13
|
1 2

4 3
|
1
3 2
|
28
|
1 2
4 3
|
1

3 2
|
14
|
1 2

4 3
|
1
3 2
|
29
|
1 2

4 3
|
1
 
3 2 2
|
15
|
1 2

4 3
|
1

3 2
|
30
|
1 2

4 3
|
1

3 2
|
18. Найдите степени всех вершин, радиус и диаметр графа G. Найдите хроматическое число графа, проведя его раскраску по методу минимальной раскраски. Является ли изображенный граф планарным?
№
|
G
|
№
|
G
|
1
|
1 2 3 4

5 6 7 8
|
16
|
1 2 3 4

5 6 7 8
|
2
|
1 2 3 4

5 6 7 8
|
17
|
1 2 3 4
  
5 6 7 8
|
3
|
1 2 3 4

5 6 7 8
|
18
|
1 2 3 4

5 6 7 8
|
4
|
1 2 3 4

5 6 7 8
|
19
|
1 2 3 4

5 6 7 8
|
5
|
1 2 3 4

5 6 7 8
|
20
|
1 2 3 4

5 6 7 8
|
6
|
1 2 3 4

5 6 7 8
|
21
|
1 2 3 4

5 6 7 8
|
7
|
1 2 3 4

5 6 7 8
|
22
|
1 2 3 4
5 6 7 8
|
8
|
1 2 3 4

5 6 7 8
|
23
|
1 2 3 4

5 6 7 8
|
9
|
1 2 3 4

5 6 7 8
|
24
|
1 2 3 4

5 6 7 8
|
10
|
1 2 3 4

5 6 7 8
|
25
|
1 2 3 4

5 6 7 8
|
11
|
1 2 3 4
5 6 7 8
|
26
|
1 2 3 4

5 6 7 8
|
12
|
1 2 3 4

5 6 7 8
|
27
|
1 2 3 4

5 6 7 8
|
13
|
1 2 3 4

5 6 7 8
|
28
|
1 2 3 4

5 6 7 8
|
14
|
1 2 3 4

5 6 7 8
|
29
|
1 2 3 4

5 6 7 8
|
15
|
1 2 3 4

5 6 7 8
|
30
|
1 2 3 4

5 6 7 8
|
19.Составив таблицы истинности, выясните, равносильны ли следующие формулы алгебры высказываний: F(X,Y,Z) и G(X,Y,Z).
№
|
F(X,Y,Z)
|
G(X,Y,Z)
|
|
1
|
 [ [ X↔((Y X↔((Y  Z)→ Z)→ (X (X  Y))] Y))]
|
(( X X  Z) Z) (X (X Z)) Z))  Y Y
|
2
|
((X→Y)Z) ((XY)↔Z)
|
(XYZ)((X→Y)Z)
|
3
|
( (X (X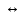 (Y (Y  Z)) Z))  X) X)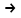 ( ( (X (X  Y) Y)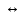 Z) Z)
|
X (Y (Y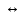 Z) Z)
|
4
|
((X^(YZ)) ¬(X ¬ Z)) ¬ (¬YZ)
|
¬(XZ) Y
|
5
|
¬ [((¬Y۷ ¬Z)↔X)۸(¬X۸(Y→ ¬Z))]
|
(X۸Y۸Z) ۷ ¬X۷ (X۸ ¬Y) ۷ (X۸Y۸ ¬Z)
|
6
|
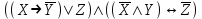
|

|
7
|

|

|
8
|
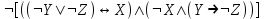
|

|
9
|
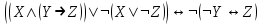
|
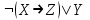
|
10
|
┐[ ┐ X ↔ ((YV┐Z) → ┐(XV ┐Y))]
|
((┐X ┐Z) V (X Z)) ┐Y
|
11
|

|
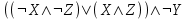
|
12
|
( (X↔(Y (X↔(Y  Z)) Z))  X)→( (X X)→( (X  Y)↔Z) Y)↔Z)
|
X (Y↔ Z) (Y↔ Z)
|
13
|
= ((X٨(Y→Z)) ٧¬(X٧¬Z)↔( ¬Y↔Z)
|
¬(X→Z) ٧Y
|
14
|
 [ [  X↔((Y X↔((Y  Z) → Z) →  (X (X  Y)) ] Y)) ]
|
(( X X  Z) Z) (X (X Z)) Z))  Y Y
|
15
|
((X→Y)Z) ((XY)↔Z)
|
(XYZ)((X→Y)Z)
| |
 Скачать 1.1 Mb.
Скачать 1.1 Mb. .
.  2.
2. 
 3. 4.
3. 4.

 . 6. 7. 8.
. 6. 7. 8.

 10.
10.





 2
2
















 2
2












 [
[
 (Y
(Y (
(