тест1. Индивидуальное домашнее задание по дискретной математике

• Название: Индивидуальное домашнее задание по дискретной математике
• Анкор: тест1
• Дата: 10.05.2023
• Размер: 1.1 Mb.
• Имя файла: IDZ_ODMiL.docx
• Тип: Документы; #1119107
• страница: 2 из 12

2. Для универсального множества U={-5,-4,-3,-2,-1, 1, 2, 3, 4, 5}, множества А, заданного списком и для В, являющимся множеством корней уравнения х⁴+х³+х²+х+=0

а) найти множества АВ, АВ,А\В, В\А, АВ, Ā, С=(АВ)А,

б) выяснить, какая из пяти возможностей выполнена для множеств АиС: АС, или СА, или А=С, или АС=, или А и С находятся в общем положении,

в) найти множество всех подмножеств множества В.

№	А					№	А				
1	-1,1,4,3	1	-12	-28	-16	16	-2,1,3,5	3	-7	-15	18
2	-1,1,2,3	7	13	-3	-18	17	-3,-1,1,2	5	1	-21	-18
3	-1,1,3,4	-2	-12	18	27	18	-2,2,3,4	2	-7	-20	-12
4	-1,1,2,3	0	-17	36	-20	19	-3,-1,2,4	-2	-15	-4	20
5	-2,1,3,4	0	-11	-18	-8	20	-3,-1,2,3	-5	1	21	-18
6	-1,1,4,5	3	-9	-23	-12	21	-4,-3,1,2	1	-7	-13	-6
7	-3,-1,1,2	-2	-7	20	-12	22	-5,-1,1,3	6	0	-22	15
8	-4,-1,1,2	0	-11	18	-8	23	-1,1,2,3	-3	-3	7	6
9	-1,1,2,3	-7	12	4	-16	24	-1,2,4,5	0	-9	-4	12
10	-2,-1,2,4	-1	-7	13	-6	25	1,2,3,4	3	-3	-7	6
11	-1,1,2,3	-4	3	4	-4	26	-1,1,2,4	1	-12	4	16
12	-1,1,2,3	-5	-3	13	10	27	-1,1,2,3	-2	-4	2	3
13	-3,3,4,5	-11	39	-49	20	28	-3,-2,-1,1	-4	-10	28	-15
14	1,2,3,4	-6	8	6	-9	29	-1,2,3,4	-4	-2	12	9
15	-2,-1,1,2	-3	-2	12	-8	30	-1,2,3,4	3	1	-3	-2

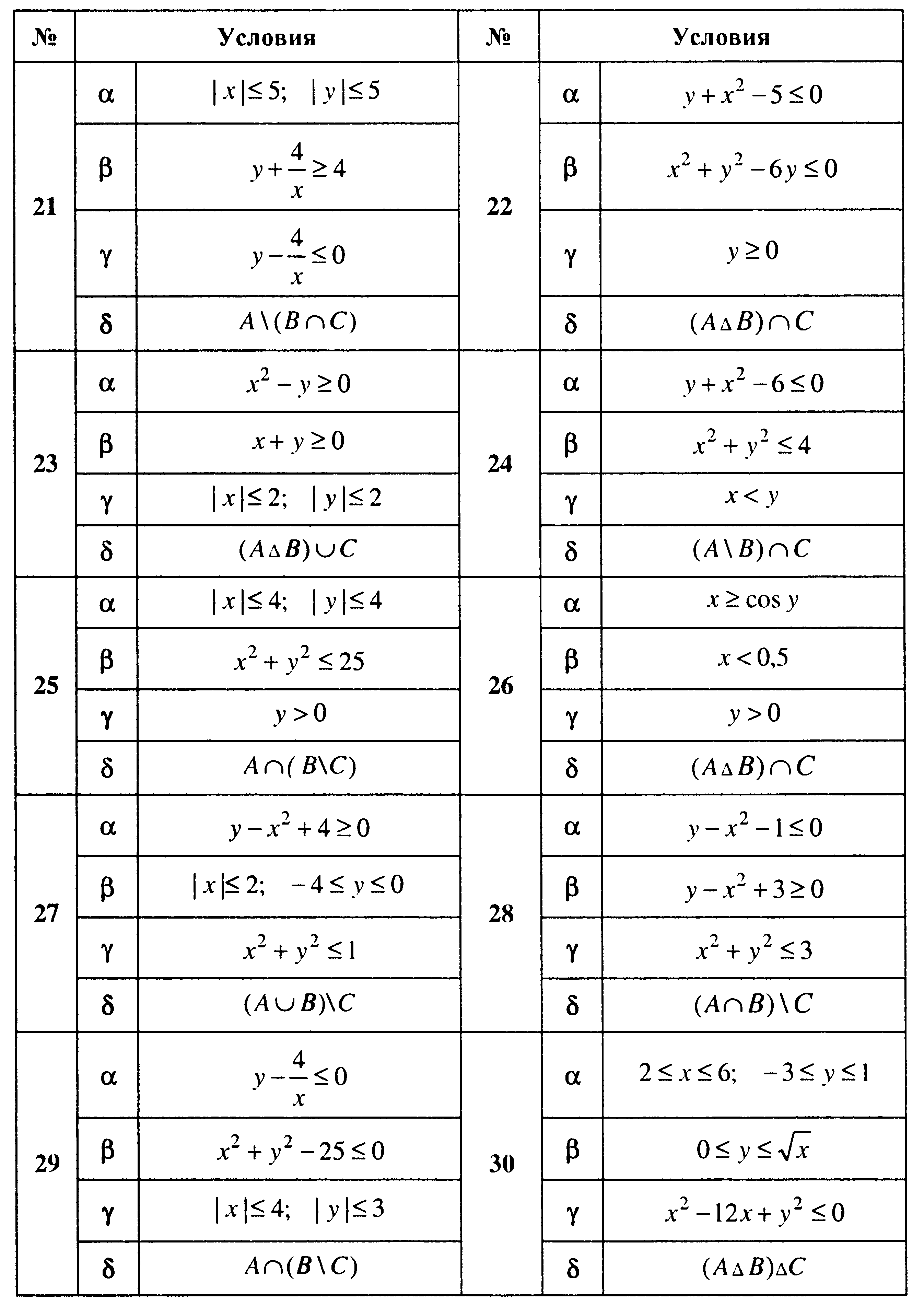
3. Пусть A, B, C, - множество точек плоскости, координаты которых удовлетворяют условиям α, β и γ соответственно. Изобразите в системе координат x0y множество D, полученное из множеств A, B и C по формуле δ.


4. Проверить справедливость равенства  для А=1,2, В=2,3, С=1,3. Выяснить, верно ли равенство  для произвольных А, В, С.

№		№	
1	АС=(А(С\В))(А(СВ))	16	BA=(B(AС))  (BA)
2	АС=(А(СВ))(АС)	17	BA=(BA)  (B(A\С))
3	А(ВС)=(А(СВ)) \ (А(СВ))	18	B(AС)=(B(A\С))  (BС)
4	АС=(А(С\В))(АС)	19	BA=(BA)(B(AС))
5	А(ВС)=(АВ) (А(С\В))	20	B(A\С)=(BA) \ (B(AС))
6	А(С\B)=(АС) (А(СВ))	21	BA=(B(AC)) \ (B(C\A))
7	АС=(А(СВ))  (АС)	22	B(AС)=(BA) \ (B(A\С))
8	А(C (ВС))=(А(СВ)) (АС)	23	B(A\С)=(BA)  (B(AС))
9	А(С\B)=(АС) \ (А(СВ))	24	B(A\С)=(BAС)) \ (BС)
10	А(ВС)=(А(ВС))  (А(СВ))	25	CB=(C(B\A))  (C(BA))
11	АС=(А(СВ)) \ (А(B\С))	26	CB=(C(BA))  (CB)
12	А(ВС)=(АС) \ (А(С\В))	27	C(AB)=(C(AВ)) \ (C(AВ))
13	А(ВС)=(А(ВС)) \ (А(ВС))	28	CB=(C(B\A))(CB)
14	А(С\B)=(А(ВС)) \ (АВ)	29	C(AB)=(CA)  (C(B\A))
15	BA=(B(A\С))  (B(AC))	30	C(B\A)=(CB) (C(AB))

5. Для данного графика Р найти: Р^-1, Р_°Р, Р^-1_°Р, пр₂(Р^-1_°Р) ´ пр₁(Р_°Р).

№	Р	№	Р
1	(1,2), (1,3), (4,2), (2,3), (3,3)	16	(c,c), (c,b), (b,b), (a,b), (c,a)
2	(2,2), (4,4), (1,2), (3,1), (3,4)	17	(e,a), (a,a), (a,e), (e,b), (b,a)
3	(1,2), (2,3), (3,1), (2,2), (3,2)	18	(f,d), (b,d), (d,d), (c,b), (f,c)
4	(3,3), (3,2), (2,2), (1,2), (3,1)	19	(a,a), (a,b), (b,c), (c,a), (c,b)
5	(0,1), (1,1), (1,0), (0,2), (2,1)	20	(a,c), (c,a), (b,b), (a,b), (a,d)
6	(5,4), (2,4), (4,4), (3,2), (5,3)	21	(c,g), (g,d), (d,d), (g,c), (d,c)
7	(1,1), (1,2), (2,3), (3,1), (3,2)	22	(e,b), (b,c), (c,c), (c,e), (e,e)
8	(3,1), (1,3), (2,2), (1,2), (1,4)	23	(a,f), (f,b), (b,b), (a,a), (a,c)
9	(3,8), (8,4), (4,4), (8,3), (4,3)	24	(e,b), (e,c), (e,e), (a,b), (b,c)
10	(0,2), (2,3), (3,0), (3,3), (0,0)	25	(x,y), (x,z), (t,y), (z,z), (y,z)
11	(1,5), (5,2), (2,2), (1,1), (1,3)	26	(y,y), (t,t), (x,y), (z,x), (z,t)
12	(0,2), (0,3), (0,0), (1,2), (2,3)	27	(x,y), (y,z), (z,x), (y,y), (z,y)
13	(а,b), (a,c), (d,b), (c,c), (b,c)	28	(z,z), (z,y), (y,y), (x,y), (z,x)
14	(b,b), (d,d), (a,b), (c,a), (c,d)	29	(t,x), (x,x), (x,t), (t,y), (y,x)
15	(a,b), (b,c), (c,a), (b,b), (c,b)	30	(w,t), (y,t), (t,t), (z,y), (w,z)