3лбEWB. Индуктивности

• Название: Индуктивности
• Анкор: 3лбEWB
• Дата: 29.10.2020
• Размер: 100.25 Kb.
• Имя файла: B-3_EWB.docx
• Тип: Документы; #146694

РАБОТА 3
КОНДЕНСАТОР И КАТУШКА ИНДУКТИВНОСТИ В ЦЕПИ СИНУСОИДАЛЬНОГО ТОКА

Цель работы. Научиться определять параметры конденсатора и катушки индуктивности с помощью амперметра, вольтметра и фазомет- ра, строить векторные диаграммы, а также проверить выполнение зако- нов Кирхгофа в цепи синусоидального тока.
Пояснения к работе

Реальный конденсатор в отличие от идеального обладает некото- рыми тепловыми потерями энергии из-за несовершенства изоляции. В расчетах электрических цепей такой конденсатор представляют обычно параллельной схемой замещения. Параметры этой схемы – g и С – мож- но экспериментально определить по показаниям амперметра I, вольт- метра U и фазометра ϕ следующим образом. Сначала найти по закону

Ома полную проводимость конденсатора

y = ^I U

, потом активную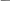

g= ycosϕ и емкостную b_C = − ysin ϕ проводимости, а затем по извест-

ной угловой частоте синусоидального напряжения сети (ω = 314 рад/с)

b_C

подсчитать емкость C = _ω .

При параллельном соединении элементов R, L, C по законам Ома и Кирхгофа в комплексной форме для входного тока имеем:

I^ɺ = I^ɺ + I^ɺ +I^ɺ =U^ɺY^ɺ ,

где

Y^ɺ = g−

jb = ye^{− jϕ}

R L C

• 
  комплексная проводимость; g – активная,
  

b = b_L − b_C

• 
  реактивная, у – полная проводимости;
  

b

ϕ = arctg

g

• 
  угол
  

сдвига фаз напряжения и тока; костная проводимости.

b_L = ¹

ωL

• 
  индуктивная, b_C= ωС – ем-
  

Напряжение на конденсаторе отстает по фазе от тока (угол сдвига

фаз ϕ < 0, b = −b_C , так как b_L= 0 ).

Угол потерь, характеризующий несовершенную изоляцию конден-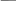

сатора, равен δ = arctg ^g

ωC

0

; очевидно, tgδ = tg(90

+ ϕ).

Реальная катушка индуктивности также обладает тепловыми поте- рями в отличие от идеальной катушки. Эквивалентную схему замеще- ния такой катушки обычно представляют в виде последовательного со- единения элементов R и L. Эти параметры можно экспериментально определить по показаниям вышеупомянутых приборов, воспользовав- шись формулами:

Z = ^U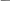

_I ,

R= Zcosϕ , X

= Zsin ϕ,

L = ^X .

ω

При последовательном соединении элементов R, L, C по законам Ома и Кирхгофа в комплексной форме входное напряжение равно:

U^ɺ = U^ɺ _R+ U^ɺ _L+ U^ɺ_C= I^ɺZ,

где Z= R + jX = Ze ^jϕ – комплексное сопротивление; R – активное,

X

Х = Х_L– Х_C– реактивное, Z – полное сопротивление; ϕ = arctg _R – угол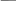

1

сдвига фаз напряжения и тока; X_L= ωL – индуктивное,

костное сопротивления.

X_C = _ωC – ем-

Ток в катушке отстает по фазе от напряжения (угол сдвига фаз

ϕ > 0, X = X_L, так как Х_C= 0). Тангенсом этого угла оценивается доброт-

ность катушки: Q_L = tgϕ =

X_{L .}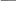

R

Подготовка к работе

1. 
   Какие физические явления отражают в схеме замещения конденсатора элементы g, C, а в схеме замещения катушки индуктивно- сти – элементы R, L?
   
2. 
   Что такое активная, емкостная, индуктивная, реактивная, полная проводимости? Как они связаны между собой?
   
3. 
   Что такое активное, емкостное, индуктивное, реактивное, полное сопротивления? Как они связаны между собой?
   
4. 
   В каких пределах может изменяться угол сдвига фаз напря- жения и тока на входе пассивного двухполюсника?
   
5. 
   Записать уравнение первого закона Кирхгофа для схемы рис. 3.1 (ключ К замкнут, 0 < R₁ < ∞) и уравнение второго закона для схемы рис. 3.2 (0 < R₁ < ∞) как для мгновенных, так и для комплексных значений токов и напряжений.
   

ИССЛЕДОВАНИЕ АКТИВНО-ЕМКОСТНОЙ ЦЕПИ

Схема электрической цепи
Схема, показанная на рис. 3.1, питается от источника синусоидаль- ного напряжения с частотой 50 Гц и действующим значением напряже- ния 100 В.

Конденсатор в схеме представлен блоком, который нужно выбрать в поле компонентов из набора cond1 ÷ cond10 по указанию преподава- теля.

Для управления положением ключа служит клавиша 1. При разо- мкнутом ключе можно по показаниям приборов определить параметры схемы замещения конденсатора, состоящей из параллельно включенных C и R.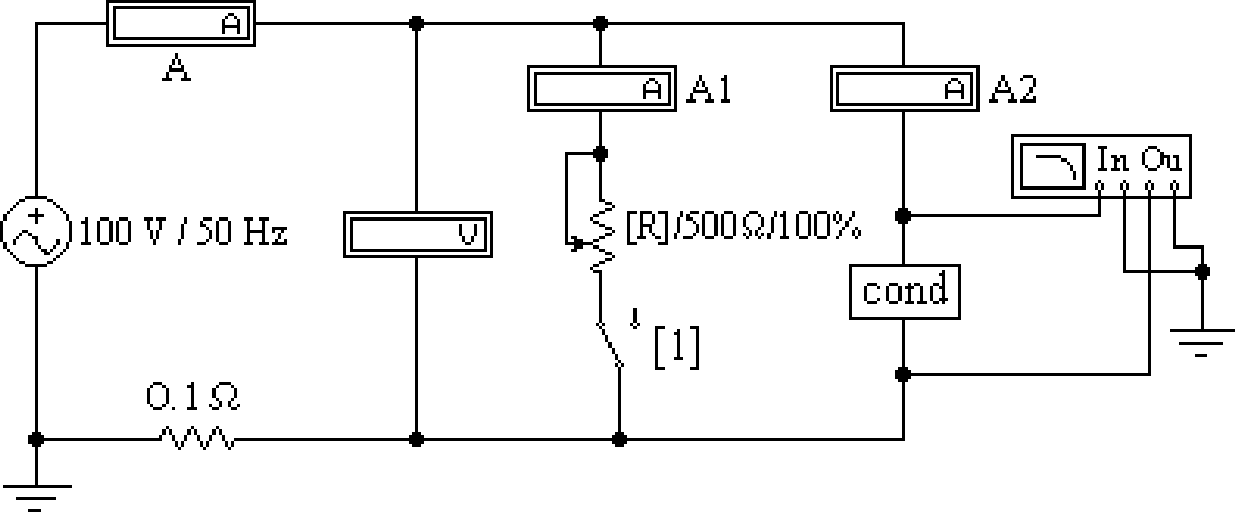




Рис 3.1
Роль фазометра в схеме исполняет прибор Bode-Plotter, пределы измерения которого от –90° до +90° уже установлены. Его нужно из- влечь из поля контрольно-измерительных приборов Instruments (у пра- вого края второй строки меню). Увеличенное изображение прибора по- является в нижней части рабочего поля после двойного щелчка левой клавишей мыши, когда курсор находится на символе прибора в схеме. При замкнутом ключе угол сдвига фаз можно изменять за счет измене- ния сопротивления реостата (управляющая клавиша R) в пределах от 500 до 50 Ом (следует избегать слишком малых значений этого сопро- тивления во избежание нарушения работы программы).
Программа работы

1. 
   Открыть файл LW3a и извлечь из поля компонентов Favor- ites блок cond, соответствующий номеру своего варианта. Собрать остальную часть схемы, показанной на рис. 3.1.
   
2. 
   Ключ с помощью управляющей клавиши 1 установить в правое положение (разомкнуть). Включить кнопку «Пуск» и записать показания приборов в верхнюю строку табл. 3.1.
   

Таблица 3.1

Данные опыта

Результаты расчета

U

I

ϕ

I1

I2

C

g

δ

Iɺ

Iɺ 1

ɺ I2

∑ Iɺ

В

А

град

А

А

мкФ

См

град

А

А

А

А

100

1.751

88.24

0

1.751

–

0

–

–

99.89

2.039

58.62

1

1.749

–

–

–

3. 
   Вычислить параметры конденсатора y, g, b_C, С, а также угол потерь δ. Записать результаты в ту же строку.
   
4. 
   Замкнуть ключ и с помощью управляющей клавиши R по-
   

добрать такое значение сопротивления реостата, чтобы обеспечить за- данную преподавателем величину угла сдвига фаз напряжения и тока на входе схемы (в пределах от -15° до -75°). Напомним, что при каждом измерении угла сдвига фаз нужно предварительно выключить и вклю- чить кнопку «Пуск». Показания приборов внести в нижнюю строку табл. 3.1.

5. 
   
   ɺ
   Принять начальную фазу входного напряжения равной ну-
   

1
лю и записать комплексные действующие значения токов I^ɺ , I^ɺ , и I₂ в

этом режиме в ту же строку. Подсчитать _∑ I^ɺ = I^ɺ + I^ɺ и сравнить ре-

1 2

зультат со значением I^ɺ , полученном в эксперименте, проверив тем са- мым выполнение первого закона Кирхгофа.

6. 
   По данным табл. 3.1 построить лучевую диаграмму токов.
   

ИССЛЕДОВАНИЕ АКТИВНО-ИНДУКТИВНОЙ ЦЕПИ
Схема электрической цепи
Схема, показанная на рис. 3.2, питается от источника синусоидаль- ного напряжения с частотой 50 Гц и действующим значением напряже- ния 100 В. Катушка индуктивности в схеме представлена блоком, кото- рый нужно выбрать в поле компонентов Favorites из набора ind1 ÷

ind10 по указанию преподавателя. Когда сопротивление реостата R₁

равно нулю, по показаниям приборов можно вычислить параметры схе- мы замещения катушки R и L.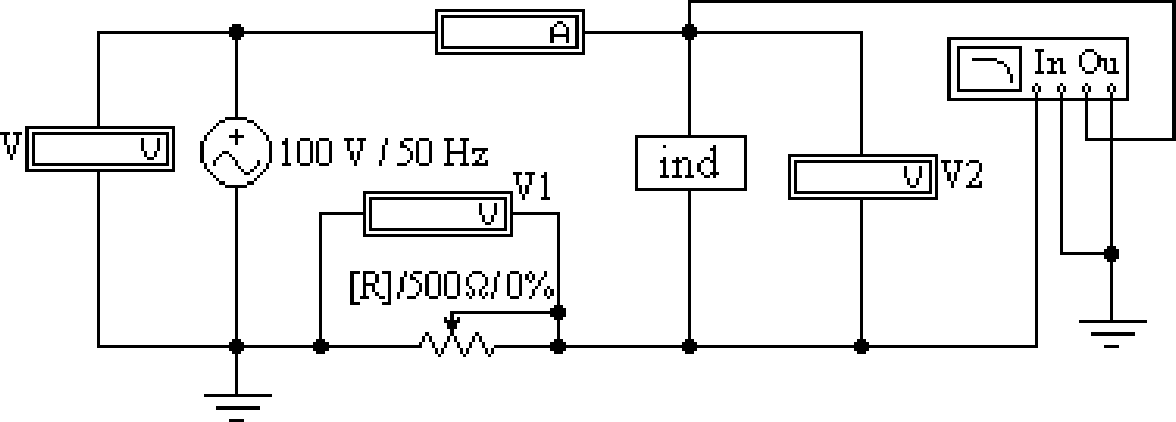



Рис. 3.2
Прибор Bode-Plotter исполняет и в этой схеме роль фазометра с теми же особенностями измерения угла сдвига фаз напряжения и тока на входе цепи. За счет изменения сопротивления реостата можно до- биться изменения угла до значения, указанного преподавателем.
Программа работы

7. 
   Открыть файл LW3b и извлечь из поля компонентов Favor- ites подсхему ind, соответствующую номеру своего варианта. Собрать остальную часть схемы, показанной на рис. 3.2.
   
8. 
   Вывести реостат с помощью управляющей клавиши R (установить R = 0). Включить кнопку «Пуск» и записать показания при- боров в верхнюю строку табл. 3.2.
   

Таблица 3.2

Данные эксперимента

Результаты расчета

U

I

ϕ

U1

U2

L

R

QL

Uɺ

Uɺ 1

Uɺ 2

∑Uɺ

В

А

град

В

В

Гн

Ом

–

В

В

В

В

100

0.617

79.19

0

100

–

0

–

–

100

0.4869

50.41

48.64

78,82

–

–

–

9. 
   Вычислить параметры катушки индуктивности R, Z , X, L, а также ее добротность Q_L. Записать результаты в ту же строку.
   
10. 
    С помощью управляющей клавиши R подобрать такое зна- чение сопротивления реостата, чтобы обеспечить заданную преподава- телем величину угла сдвига фаз напряжения и тока на входе схемы (в
    

пределах от 15° до 75°). Напомним, что при каждом измерении угла сдвига фаз нужно предварительно выключить и включить кнопку

«Пуск». Показания приборов внести в нижнюю строку табл. 3.2.

11. 
    Принять в этом режиме начальную фазу входного тока рав- ной нулю и записать комплексные действующие значения напряжений
    

1

2

1 2
U^ɺ , U^ɺ , и U^ɺ в ту же строку. Подсчитать _∑U^ɺ = U^ɺ + U^ɺ и сравнить ре-

зультат со значением U^ɺ , полученном в эксперименте, проверив тем са- мым выполнение второго закона Кирхгофа.

12. 
    По данным второй строки табл. 3.2 построить топографиче- скую диаграмму напряжений.
    
13. 
    Сделать общие выводы по работе.
    

РАБОТА 4
ИССЛЕДОВАНИЕ ЦЕПЕЙ С ИНДУКТИВНО СВЯЗАННЫМИ

ЭЛЕМЕНТАМИ
Цель работы. Научиться определять параметры катушек индук- тивности с помощью амперметра, вольтметра и ваттметра. Провести экспериментальное исследование цепей с последовательным и парал- лельным соединением индуктивно связанных катушек. Научиться опре- делять взаимную индуктивность катушек и строить векторные диа- граммы для цепей с индуктивной связью.
Пояснения к работе
Реальная катушка индуктивности без ферромагнитного сердечника обычно бывает представлена схемой замещения из последовательно со- единенных идеальной индуктивности и активного сопротивления. Па- раметры этой схемы могут быть определены по показаниям амперметра, вольтметра и ваттметра с помощью формул:

P U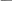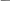

R = _{I 2} , Z = _I , _{X =}

L = ^X


.
, _ω

При последовательном соединении катушек полное сопротивление цепи находится как

Э Э

Э 1 2
Z= R² + X ² , R

= R + R , X

= X + X .

Э 1 2
Если часть Ф₂₁ магнитного потока Ф₁₁, созданного током i₁ в одной из катушек с числом витков w₁, пронизывает другую катушку с числом витков w₂, или, наоборот, часть Ф₁₂ потока второй катушки Ф₂₂, создан- ного током в ней i₂, пронизывает первую, то эти частичные потоки называются потоками взаимоиндукции, а полные потоки (Ф₁₁, Ф₂₂) – потоками самоиндукции. Потокосцепления этих потоков с соответ- ствующими катушками равны:

ψ₁₁ = w₁ Ф₁₁ , ψ₂₂ = w₂ Ф₂₂ , ψ₁₂ = w₁ Ф₁₂ , ψ₂₁ = w₂ Ф₂₁ ,