курсовая типис. курсовая усов а в. Информационные меры Ю. Шрейдера Этапы развития ис Выполнил студент Усов А. В

• Название: Информационные меры Ю. Шрейдера Этапы развития ис Выполнил студент Усов А. В
• Анкор: курсовая типис
• Дата: 25.06.2021
• Размер: 135.73 Kb.
• Имя файла: курсовая усов а в.docx
• Тип: Курсовая; #221441
• страница: 3 из 6

1.4.3 Окрестностные грамматики и окрестностные языки

Как уже говорилось, простейшая окрестностная грамматика – это конечный набор окрестностей некоторого типа. Окрестностный язык, задаваемый такой грамматикой, – это множество деревьев, у каждой вершины которой найдется окрестность из данного набора. Например, каждой бесконтекстной грамматике можно сопоставить набор описанных выше «кустов»: например, правилу типа P → QPb сопоставляется куст, изображенный в левой части рис. 5, а каждому терминальному символу – тривиальную окрестность (см.

правую часть рис. 5). Такая грамматика задает окрестностный язык, содержащий все синтаксические структуры, определяемые исходной бесконтекстной грамматикой. Таким образом, окрестностные грамматики – это тоже аксиомы. выполняющиеся на текстах окрестностного языка. Их можно представить и в виде «обычных» формул языка первого порядка. Но окрестностное представление более структурировано и наглядно. Итак, аксиомы, задающие знаковую систему, вместе с каждой окрестностной грамматикой, определяют окрестностный язык, как аксиоматический класс моделей.

1.5 Количество информации по Ю. Шрейдеру

1.5.1 Ранговые распределения как системное свойство

Уже к 50-м годам стало понятным, что многие статистические закономерности, наблюдавшиеся в различных социальных явлениях и получившие названия в честь их первооткрывателей (Ципфа, Эступа, Парето, Брэдфорда и др.), имеют общую математическую форму.

Эти закономерности удобно формулировать как некоторые свойства ранговых распределений. Именно с последнего понятия удобно начать дальнейший разговор, ибо само понятие рангового распределения допускает обобщенную формулировку, применимую при определенных ухищрениях ко всем случаям, где возникают те закономерности, которые сегодня чаще всего называют "законом Ципфа".

Основным объектом нашего рассмотрения является текст, понимаемый как список вхождений словоформ. Каждой словоформе соответствует некоторое слово. Совокупность (или список) всех слов, соответствующих словоформам, образующих текст Т, мы будем называть словарем V данного текста. Для каждого слова W из словаря V мы можем указать целое число n(W), равное количеству имеющихся в тексте Т словоформ, которым соответствует данное слово W. Величину n(W) уместно назвать встречаемостью слова W в тексте Т.

Ясно, что общая сумма встречаемости слов равна общему количеству словоформ N в тексте Т или объему этого текста: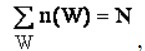



где сумма берётся по всем словам, входящим в словарь V данного текста. Упорядочим теперь слова в словаре по убыванию величин n(W). Номер слова в таком списке назовём рангом К, а само слово ранга К мы будем обозначать W_k (порядок слов, имеющих одинаковую встречаемость, будем обозначать произвольно в пределах этого значения n(W) встречаемости. Важно лишь то, что разные слова получают разные ранги). Итак ранги, приписываемые словам в словаре, принимают значения от 1 до М, где М-объём словаря, т.е. общее количество слов в словаре.

Эта система понятий как общая схема описания ранговых распределений была введена нами в работе [1].

Пример I. Текст Т - это реальный письменный текст на русском, английском и т.д. языке. Словоформой называется последовательность букв между двумя пробелами, то есть вхождение формы слова в тексте, являющееся грамматической формой некоторой словарной единицы W соответствующего языка. Встречаемость W в тексте Т это общее количество соответствующих этой словарной единице словоформ в данном тексте.

Примечание. Можно по-разному определять, что является формой данного слова (словарной единицы). Например, является ли отглагольное существительное "ожидание" словоформой слова "ожидать" или самостоятельным словом? Ю.К.Орлов [2] при анализе былины вынужден был принять слово "ратай" (пахарь) формой слова "оратай".

Пример II. Текст Т состоит из списка видов некоторого семейства в биологической классификации. Словоформой является название вида из этого списка, а словом - название рода, к которому этот вид принадлежит.(Видовое латинское название состоит из имени рода и имени вида). Встречаемость слова - это количество видов в данном роде. Здесь каждая "словоформа" имеет одно вхождение.

Пример III. Текст Т состоит из списка предприятий [3,4] с указанием вида деятельности этого предприятия. Словом мы будем считать название вида деятельности, а его встречаемость равна количеству предприятий, выполняющих эту деятельность.

Введём теперь частоту слова W_к как частное

Из равенства (1) следует, что , а это уже даёт недвусмысленный намёк, что величина Р_к - это частоты появления случайных событий, приближённо совпадающих с некоторыми вероятностями событий, возникающих в рамках какого-то стохастического механизма. Фактически открытие закона Ципфа состояло в том, что, грубо говоря, эти величины Р_к с возрастанием ранга убывают обратно пропорционально рангу:

. (2)

Это эмпирическое наблюдение, основанное как на материале текстов на естественном языке, так и на материале обобщённых текстов, дало толчок к поиску стохастических механизмов, обеспечивающих появление закономерностей типа (2). Так, широкое распространение нормального закона распределения объясняется тем, что он возникает при суммировании большого количества примерно равновеликих и слабо коррелированных случайных величин. Это уже даёт основание в ряде случаев ожидать появления нормальных распределений. Такая аналогия стимулирует поиск вероятностных механизмов, генерирующих тексты с частотами слов, распределёнными по закону Ципфа или близкими к нему. Такой объясняющий "ципфиаду" механизм был предложен Б.Мандельбротом [5]. В основе этого результата лежит предположение, что текст появляется как результат случайного выбора составляющих его слов с вероятностями, определяемыми количеством букв в данном слове. Мне удалось показать [1], что этот результат фактически основан на некоторых предположениях о "сложности" слова, определяющей его встречаемость в тексте. Тем самым можно было объяснить закономерность появления "ципфиады" более релевантными, чем число букв, характеристиками сложности слова (например, его семантическими свойствами) и перенести этот результат на тексты общей природы. Но сама вероятностная парадигма оказалась недостаточной, чтобы обосновать более тонкие закономерности ранговых распределений: наличие большого количества слов единичной встречаемости ("ноева каста" - по терминологии Б.И.Кудрина [6]), связь объёма текста N и объёма его словаря М и др. Более того, Ю.К.Орлов [2], обративший впервые внимание на значимость этих моментов, указал и на то, что качество выполнения закона Ципфа для данного текста определяется не его объёмом, но свойством быть целостным текстом. Последнее уже явно не согласуется с вероятностной парадигмой, требующей, чтобы увеличение выборки влекло за собой улучшения соответствия между наблюдаемыми частотами и теоретически предсказанными вероятностями событий. Таким образом, если стохастические механизмы генерирования текста даже существуют в реальности, то они не являются общеязыковыми, но выбираются (кем? как?) каждый раз специально для порождения данного конкретного текста. Изложенные соображения послужили основанием для того, чтобы искать природу появления ранговых распределений не в стохастических механизмах порождения текстов, но в системных свойствах целостных текстов. Изменение представления о самой природе явления привело к изменению используемых для его изучения методов. В этом проявился принцип методологического порочного круга [7, с.25]: "Методы научного познания характеризуются определёнными познавательными установками, опирающимися на онтологические представления о природе изучаемой действительности. В свою очередь использование этих методов позволяет познавать только те фрагменты действительности, которые удовлетворяют исходным

онтологическим представлениям."

Нам пришлось сменить онтологические представления о текстах, как о результатах действия стохастических механизмов генерации, на представления об их системной природе, что привело к использованию совсем иного подхода в анализе "ципфиады". Более того, оказалось естественнее рассматривать текст как законченный целостный продукт, а не как неопределённо долгий процесс порождения. Впрочем, на конференции рассматривались ситуации с текстом, обладающим динамикой развития. Но характерно, что для этих ситуаций пришлось ввести дополнительный параметр. Вероятно, что попытка описать строение таких текстов с помощью каких-то принципов оптимума приведёт к рассмотрению чего-то вроде "градиента диссимметрии".

Соответствующие результаты для целостных (завершенных) текстов нами [8] были сформулированы в виде "принципа максимума диссимметрии" текста как системы, из которой были строго выведены не только "ципфовские", но и "орловские" закономерности возникающего рангового распределения, включая связь объёма текста с объёмом словаря, а также связь встречаемости первого слова с количеством слов единичной встречаемости. Этот вывод оказался достаточно изощрённым и потребовал серьёзных усилий и выдумки. Однако, использование данного принципа само по себе ставит новые вопросы.

Прежде всего сам текст - это не система, но продукт деятельности системы - человека или человеческого сообщества. В случае примера II текст оказывается продуктом деятельности биологической эволюции. Ясно, что человек, продуцируя свой текст, не заботится сознательно о соблюдении принципа максимума диссимметрии - этот принцип обнаруживает исследователь текста. Соблюдение этого принципа есть косвенный результат деятельности системы. Действия человека как системы вообще не определяются целями (такая "целеориентированность" есть скорее свойство "машинного интеллекта" - см. [9]), а человеку свойственно ориентироваться на ценности, выбирать между тем, что хорошо, и тем, что дурно.

Здесь появляется одно тонкое и весьма принципиальное обстоятельство. Реальный выбор между добром и злом возможен только в том случае, когда этот выбор не предопределяется ни действующими на субъект (систему) причинами, ни поставленной перед ним чётко определённой целью. Ориентация на ценности предполагает некое пространство свободы, в котором выбор не определяется полностью воздействующими естественными факторами, но в нём существенно задействована свободная воля субъекта - способность выбирать свои предпочтения "ни по чему", но по личному произволу. Этот произвол воли вступает в сложное взаимодействие с объективными обстоятельствами, поэтому фактически свободный выбор, совпадающий с намерением воли, осуществляется не всегда, но при определённых условиях, что продемонстрировано на модели, о которой пойдёт речь ниже.

Проблема, на мой взгляд, состоит в том, чтобы показать как действие системы, осуществляющей ценностный выбор на основе свободной воли, способно приводить к порождению текстов, удовлетворяющих максимуму диссимметрии. В этом случае мы отходим от представления о случайности, порождаемой свободным выбором во взаимодействии с другими факторами. Реалистичность решения поставленной проблемы подтверждается тем, что уже существует математическая модель ситуации ценностного выбора, в которой свободная воля субъекта играет существенную роль. Эта модель разработана В.А.Лефевром [10] и применена им к анализу большого количества ситуаций выбора. Ниже я излагаю модель Лефевра в несколько отличной от авторской интерпретации.

Сам Лефевр рассматривает ценности различной природы, но мне удобнее здесь рассуждать об этическом выборе. Именно в этом случае наличие свободной воли у человека играет принципиальную роль, так как только при этом предположении имеет смысл говорить об ответственности человека за свои поступки. Если же действия субъекта предопределены объективными (природными) причинами и неотменяемыми целями, то ни о какой ответственности речи быть не может. (Собственно, в этом случае бессмысленно говорить о поступках, ибо действия человека в этом случае полностью вынуждены чем-то, находящимся вне его личности).

Мы будем рассматривать акт выбора субъектом одного из двух полюсов: негативного и позитивного. Принцип "этической доброкачественности" субъекта состоит в том, что субъект выбирает негативный полюс только под влиянием соблазна, исходящего от внешней среды или из глубин подсознания. Обозначим через х₁ вероятность отсутствия такого соблазна. Субъект может осознать наличие соблазна с вероятностью 1-х₂. В этом случае мы будем говорить, что совесть указывает на наличие соблазна. Далее вступает в действие свободная воля субъекта, который выбирает величину х₃-свой уровень готовности соглашаться с предупреждением совести. (Если такого предупреждения не поступает, то субъект никакого решения не принимает, но слепо следует соблазну, либо, в отсутствие такового, автоматически выбирает позитивный полюс).

Будем считать, что в распоряжении субъекта имеется генератор равномерно распределённых на отрезке (0,1) случайных чисел. Субъект получает от генератора число z и, если z<х₃, поступает так, как ему велит совесть. Вероятность этого равна х₃. Легко видеть, что вероятность выбора субъектом положительного полюса (реакция субъекта) по формуле полной вероятности равна

X ₁ = ( 1 - x₁ ) ( 1 - x₂ ) x₃ + x₁ , (3)

что совпадает с "формулой человека" в цитированной работе Лефевра. Этот вывод отличается от вывода самого Лефевра, в частности, отсутствием одного из используемых им положений.

Свобода воли в этой модели реализуется в том, что субъект независимо от внешних воздействий и собственного состояния свободно назначает свою готовность повиноваться голосу совести. Но эта готовность, вообще говоря, не совпадает с вероятностью выбора позитивного полюса. Различие между реакцией субъекта х₁ и готовностью х₃ связано с тем, что по свободной воле субъект реагирует на предупреждения голоса совести об имеющемся соблазне, а в ситуации, когда голос совести молчит или когда соблазн вообще отсутствует, тот фрагмент сознания, где действует свободная воля, вообще не включается.

Субъект, с которым соотнесена описываемая модель, имеет всегда возможность сделать "реалистический выбор", назначив вероятность х₃ так, чтобы она совпала с вероятностью Х₁ выбрать позитивный полюс ("добро"). Но свободный выбор он делает только, когда его реакция тождественно совпадает с его готовностью, т.е. когда Х₁=х₃. Вообще говоря, такое совпадение имеет место лишь при одном значении х₃, отвечающем "реалистическому выбору". Случай, когда уравнение Х₁=х₃ обращается в тождество - это свободный выбор. Он имеет место в случае х₁=х₂=0, т.е. когда соблазны с вероятностью 1 и с той же вероятностью замечаются совестью, в этом случае готовность повиноваться совести совпадает с вероятностью выбора позитивного полюса.

Естественно предложить в качестве "меры несвободы выбора" максимум по всем х₃ вероятностям отклонения готовности действовать по совести от вероятности позитивного выбора (качества реакции субъекта):

a=max ½X₁-x₃½=max(x₁,(1-x₁)x₂). (4) x₃