курсовая типис. курсовая усов а в. Информационные меры Ю. Шрейдера Этапы развития ис Выполнил студент Усов А. В

• Название: Информационные меры Ю. Шрейдера Этапы развития ис Выполнил студент Усов А. В
• Анкор: курсовая типис
• Дата: 25.06.2021
• Размер: 135.73 Kb.
• Имя файла: курсовая усов а в.docx
• Тип: Курсовая; #221441
• страница: 2 из 6

1.3 Примеры знаковых систем

1.3.1 Деревья непосредственно составляющих

Пример дерева непосредственных составляющих приведен на рис. 1 и чуть более абстрактный пример – на рис. 2. Чтобы представить такие деревья как конечные модели (т.е. тексты в нашей терминологии), нужно описать их несущие множества и сигнатуру ΩICTr отношений, определенных на этих множествах. Несущее множество дерева – это множество его вершин.

Отношения удобно разделить на три части: ΩICTr = ΩTr ΩOrd ΩLbl. Отношения 12 из ΩTr представляют структуру «собственно» дерева, отношения из ΩOrd отвечают за порядок «слева-направо», а отношения из ΩLbl представляют ярлыки (терминальные и нетерминальные символы), метящие вершины дерева.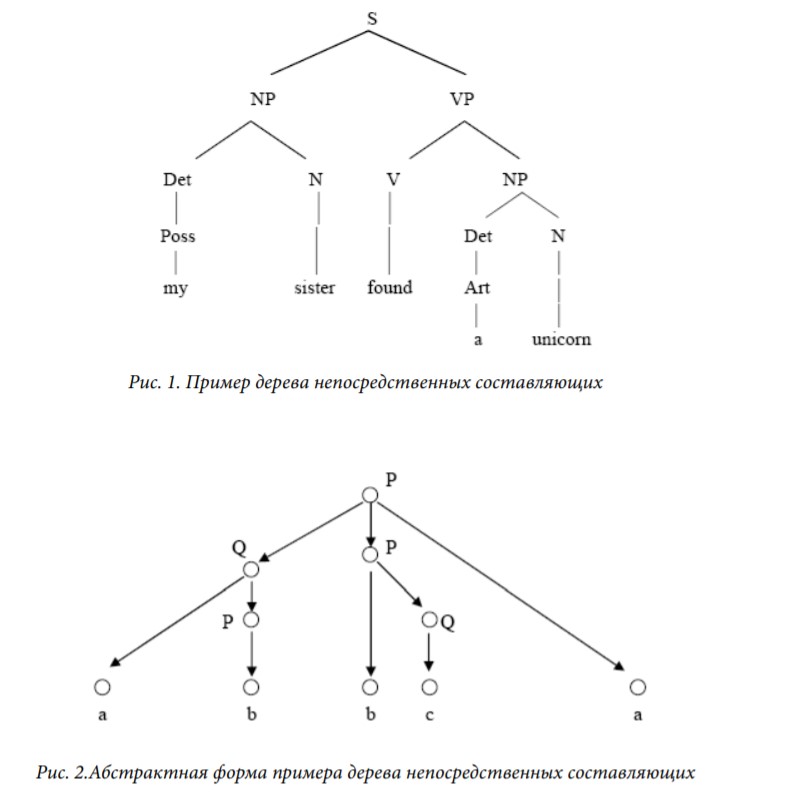



ΩTr = {↓, ⇓, Root, Leaf}1 , где ↓ и ⇓ – бинарные отношения, ↓ – отношение непосредственной доминации, ⇓ – отношение строгого частичного порядка, транзитивное замыкание отношения ↓ (и, конечно, ↓ – транзитивная редукция отношения ⇓). Дерево непосредственных составляющих должно быть деревом по отношению ↓ в смысле теории графов. Root и Leaf – унарные отношения, Root метит корень дерева, а листья помечены Leaf. ΩOrd = {→, ⇒}состоит из двух бинарных отношений: ⇒ – отношение строгого частичного порядка (слева направо) на вершинах дерева и → – транзитивная редукция ⇒, соотносящая «непосредственных соседей». Два частичных порядка ⇓ и ⇒ соотносятся естественным образом. Использованная здесь нотация отражает «перпендикулярность» этих отношений, их точное соотношение описывается обычно аксиомами «дополнительного распределения» и «несмешения составляющих» (exclusivity and non-tangling conditions). Как уже говорилось, отношения из ΩLbl представляют терминальные и нетерминальные символы. На «картинках» при изображении деревьев непосредственных составляющих (см. рис. 1 и 2 выше) обычно линиями или стрелочками изображается только отношение ↓. Аксиомы, выделяющие знаковую систему деревьев непосредственных составляющих (множество всех деревьев) из множества всех текстов в сигнатуре ΩICTr, легко записать на языке логики первого порядка.

1.3.2 Слова, деревья зависимости и другие примеры

Приведу с минимальными комментариями примеры текстов, представляющих слова в некотором алфавите (рис. 3), и деревья зависимостей (рис. 4).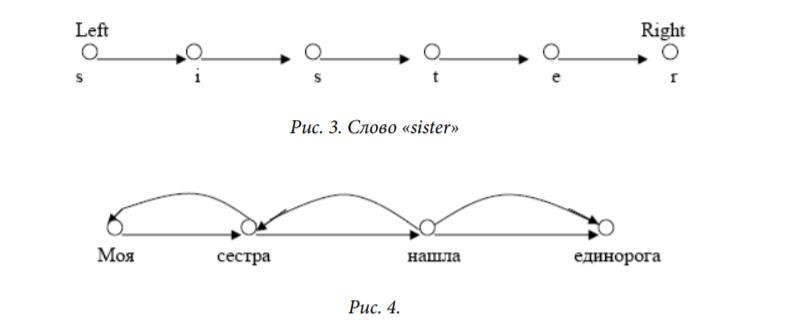



Несущее множество каждой модели (текста), представляющей некоторое слово в данном алфавите, состоит из вершин, представляющих вхождения букв в это слово. Сигнатуру ΩStr отношений таких моделей естественно разделить на две части: ΩStr = ΩLOrd ΩTLbl Отношения из ΩLOrd, подобно отношениям из ΩOrd выше, представляют порядок «слева-направо», ΩLOrd =

{→, ⇒, Left, Right}, только здесь ⇒ – это отношение линейного порядка, а → – его редукция; унарные отношения Left и Right метят «крайние» вхождения. Отношения из ΩTLbl представляют буквы алфавита. Деревья зависимостей (графы Теньера) представляют грамматические зависимости на словах предложения. В таких деревьях нет нетерминальных вершин. Сигнатура ΩDT этой знаковой системы – это, грубо говоря, смесь отношений из рассмотренных выше сигнатур ΩICTr and ΩStr, ΩDT = ΩTr ΩLOrd ΩTLbl.

1.4 Окрестностные грамматики и языки

1.4.1 Окрестности и типы окрестностей

Как уже говорилось, мы выделяем языки внутри знаковой системы, описывая локальные свойства их текстов. Мы рассматриваем окрестности вершин текстов, разные типы таких окрестностей и окрестностные грамматики. Говоря неформально, окрестность вершины текста – это некоторый подтекст, содержащий эту вершину. Окрестностная грамматика накладывает ограничения на возможные окрестности вершин текста. Текст принадлежит языку, задаваемому грамматикой, если для каждой его вершины выполняются эти ограничения. В самом простом случае, окрестностная грамматика – это набор допустимых окрестностей и текст принадлежит языку, если у каждой вершины есть окрестность из этого набора. Я ограничусь здесь неформальным описанием примеров для деревьев непосредственных составляющих.

1.4.2 «Кусты» и другие окрестности для деревьев

Простейшие окрестности для деревьев непосредственных составляющих – это «кусты». Такая окрестность для каждой вершины x содержит эту вершину (центр окрестности, на рисунках черный кружок) 15 и все ее непосредственные составляющие (если они есть), т.е. каждую вершину y, такую, что ↓(x, y) – см. рис. 5.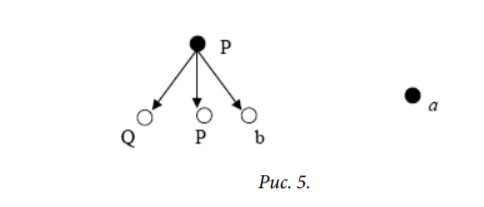



Рассматривались и другие типы окрестностей, например, произвольные поддеревья, содержащие данную вершину (см. рис. 6).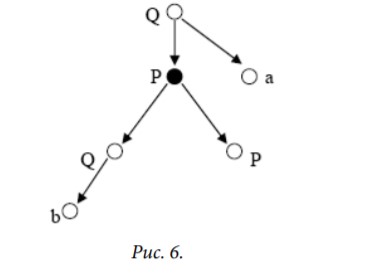