Тема: Создание таблиц значений функций, графиков и диаграмм.
Цель работы: познакомиться с возможностью Excel для проведения моделирования физических процессов, отработать умения в построении диаграмм.
Студент должен знать:
-1- методику оформления вычислительной таблицы;
-1- порядок применения формул и стандартных функций;
-1- графические возможности электронной таблицы; уметь:
-1- строить простейшие информационные модели;
-1- приводить модели моделирования;
-1- вводить информацию и редактировать электронные таблицы;
-1- применять относительные и абсолютные ссылки при выполнении вычислений;
-1- работать с деловой графикой электронной таблицы.
Теоретическое обоснование.
Моделирование равномерного движения тела.
Рассмотрим моделирование такого физического процесса, как движение тела с некоторой постоянной скоростью V = const. Поскольку ни одна из характеристик скорости (направление и величина) не изменяется, движение будет происходить вдоль прямой линии, т.е. является прямолинейным. Совместим с этой прямой ось ОХ. Каждую секунду координата х тела будет получать одно и то же приращение, поэтому в любой момент времени может быть найдена как х = vх • t, где v - проекция вектора скорости на ось ОХ. Если в
начальный момент времени (t0 = 0) положение тела не совпадало с началом отсчета, то уравнение будет иметь вид: x(t) = xo + v х • t.
Проекция вектора скорости - величина алгебраическая, т.е. она может быть и положительной, и отрицательной в зависимости от того, какой угол а образует вектор скорости с направлением оси ОХ. Г рафическое моделирование процесса равномерного прямолинейного движения будет заключаться в построении графика зависимости х = f(t) при различных значениях и направлениях скорости.
Моделирование движения тела, брошенного под углом к горизонту.
Рассмотрим случай движения тела, брошенного под углом к горизонту, происходящего только под действием силы тяжести (трением пренебрегаем!).
В этом случае одной координаты для описания движения недостаточно. Необходимо ввести систему координат хОу, при этом ось Ох направляют горизонтально, а ось Oy - вертикально вверх или вниз. Теперь положение тела задается двумя координатами (х, y), каждая из которых с течением времени будет изменяться. Закон изменения координат можно установить из следующих соображений. Поскольку мы считаем, что никакие силы, кроме силы тяжести на
1
тело не действуют, движение вдоль оси Ox будет равномерным, и абсцисса тела меняется по закону x = vxt , Сила тяжести, действующая на тело, сообщает ему ускорение g , направленное, как и сама сила, вертикально вниз. При заданной начальной скорости Vo и угле бросания А значения координат дальности полета Х и высоты Y от времени можно описать следующими формулами:
X=V0 *COS(A)*t
Y=Vo* SIN(A)*t-g*t2/2
Прежде, чем приступить к работе с таблицей, разберите ее строение, расположение исходных данных и основные формулы, используемые в расчетах. Помимо указанных формул будут использованы и некоторые дополнительные для вычисления промежуточных величин, таких как интервалы времени, приращение координаты, перевод градусной меры в радианы и т.д, о них мы поговорим позже.
Занесение формулы в ячейку начинается с ее объявления - нажатия клавиши "=" на клавиатуре. В качестве аргументов формул, записываемых в ячейки, мы будем использовать ссылки (относительные или абсолютные) на ячейки, содержащие нужные нам числовые данные, а также числа (например, показатель степени, коэффициенты при аргументах и т.д). Ввод ссылок в формулу можно проводить «вручную» с клавиатуры или выбирать с помощью мыши. Для этого достаточно щелкнуть мышкой в соответствующей ячейке и ее адрес появится в создаваемой вами формуле. Содержимое текущей (выделенной) ячейки отображается в поле ввода строки формул.
Ход работы.
Изучить теоретическое обоснование.
Выполнить практические задания.
Оформить отчет.
Ответить на вопросы по указанию преподавателя.
Практические задания:
Задание №1. Составить конспект по учебнику И. И. Сергеева стр. 187-191 (§7.47.5).
Задание №2. Задача 1.
Создание таблицы-шаблона с помощью Microsoft Excel.
На рабочем листе заполнить таблицу исходными данными, расчетными формулами и построить график равномерного движения.
Судя по уравнению движения тела, исходными данными для данной модели будут:
начальное положение (координата) тела,
проекция скорости на выбранную ось,
временной интервал (задаваемый начальным и конечным моментом времени), в течение которого рассматривается движение (время протекания процесса).
2
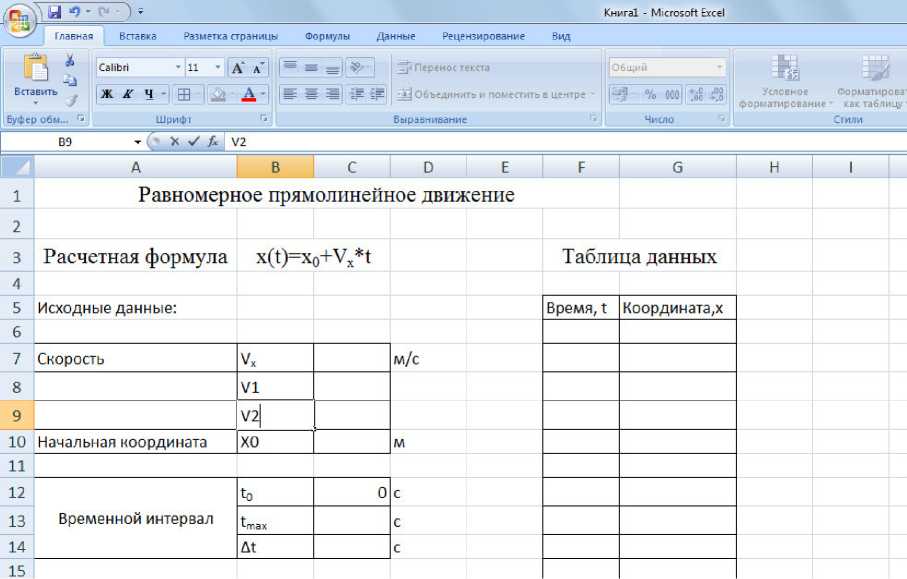
Заполнение таблицы
Занести исходные числовые данные в следующие ячейки:
скорость равномерного движения - в С7;
начальное положение тела - в С10;
конечный момент времени - в С13.
Начальный момент времени (ячейка С12) принимается равным нулю
В ячейку С14 ввести формулу, позволяющую рассчитать интервал времени
At = t max 'mm : =(С13-С12)/20
n
Здесь число 20 означает количество интервалов n, на которое разбивается выбранный промежуток времени tmin ^ tmax. Таким образом, наша таблица будет
содержать n +1 = 21 точек.
Заполнить таблицу данных:
В ячейку F6 занести начальный момент времени: =С12
Такой способ копирования устанавливает связь между ячейками (в данном случае между ячейками F6 и С12).
Ячейка F7 должна содержать момент времени, отличающийся от
предыдущего на величину интервала At : ti =ti 1 + At. Поэтому в ячейку F7 необходимо ввести: =F6+$C$14
Скопировать формулу для вычисления времени в остальные ячейки колонки таблицы с заголовком «Время, с»
Ячейка G6 должна быть связана с ячейкой С10, содержащей начальную
координату тела. Ввести в G6: =С10
В этом случае при изменении данных в ячейке С10 автоматически
3
изменится и содержимое связанной с ней ячейки G6.
В ячейку G7 занести формулу, позволяющую рассчитать координату в соответствующий момент времени: хг = x0 + v xtt
=$G$6+$C$7*F7
Скопировать формулу из ячейки G7 в диапазон ячеек G8:G26
Изменить имя листа, содержащего таблицу (в шаблоне, он назван «Лист 1»): в контекстном меню по ярлыку листа выбрать команду Переименовать и ввести с клавиатуры новое имя «Равномерное движение». После окончания ввода необходимо нажать клавишу {Enter} или щелкнуть мышкой в рабочем поле листа.
Построение графика зависимости x(t)
Выделить диапазон ячеек F6:G26, содержащих данные для построения графика. Значения в столбце F (диапазон F6:F26) будут откладываться по оси OX (ось времени), значения в столбце G (диапазон G6:G26) - по оси OY.
Выбрать команду Вставка-Диаграмма...
Выбрать тип диаграммы Точечная и вид «Точечная диаграмма со значениями, соединенными сглаживающими линиями»..
Задать параметры диаграммы ввести название диаграммы и наименование осей координат с указанием единиц измерения величин, откладываемых по этим осям:
в поле Название диаграмм - «График равномерного движения»;
в поле Ось Х (категорий) - «Время t, с»;
в поле Ось Y (значений) - «Координата х, м»
Отформатировать числовые данные в таблице, назначив диапазону F6:G26 числовой формат с двумя десятичными знаками после запятой.
вариант
|
Скорость
V0
|
Начальная
координата,
Х0
|
Временной
интервал
|
1
|
5
|
0
|
8
|
2
|
8
|
5
|
10
|
3
|
9
|
0
|
11
|
4
|
3
|
6
|
5
|
5
|
6
|
0
|
9
|
6
|
7
|
2
|
15
|
7
|
15
|
0
|
10
|
8
|
12
|
5
|
11
|
9
|
10
|
0
|
12
|
10
|
8
|
1
|
20
|
4
Задание №3. Задача 2.
Создание таблицы-шаблона с помощью Microsoft Excel.
На рабочем листе заполнить таблицу исходными данными, расчетными формулами и построить график равномерного движения тела, брошенного под углом к горизонту
Судя по уравнению движения тела, исходными данными для данной модели будут:
начальная скорость тела,
углы (в градусах)
ускорение свободного падения
3) временной интервал (задаваемый начальным и конечным моментом времени), в течение которого рассматривается движение (время протекания процесса).
-v
Книга! - Microsoft Excel
Главная Вставка Разметка страницы Формулы Данные Рецензирование Вид
*
|
III
llli
III
у
1
|
СайЬп - 11 ■ А‘ А'
|
ж JE- ч ЕВ а»-д-
|
= = = f# ;il
|
Шрифт
|
|
- J
Буфер обм... Ч
[=jJ Перенос текста
jrjbl Объединить и поместить в центре ■г Выравнивание *3
Общий
а - % 100 35 £5
Условное Форматировать Стили форматированиет кактаблицу^ ячеек-" Стили
а Я ВЛ
Вставить Удалить Формат
Ячейки
*1
|
A В
|
С D Е
|
F
|
G
|
Н
|
|
1
2
3
4
|
Движение тела, брошенного под углом к горизонту
Расчетная формула Х=У0*СО5(Л):Л Таблица данных
Y=V0*SIN(A)*t-g*tA2/2
|
|
|
5
|
Исходные данные:
|
|
|
|
Время, t
|
Координата,х
|
Координата,у
|
6
|
|
|
|
|
|
|
|
|
7
|
Скорость
|
Vo
|
|
м/с
|
|
|
|
|
8
|
Угол
|
А
|
|
|
|
|
|
|
9
|
Усокрение свободного падения
|
§
|
|
м/сЛ2
|
|
|
|
10
|
|
|
|
|
|
|
|
|
11
|
Временной интервал
|
to
|
0
|
С
|
|
|
|
|
12
13
|
tmax
|
|
с
|
|
|
|
|
At
|
|
с
|
|
|
|
14
|
|
|
|
|
|
|
Заполнение таблицы
Занести исходные числовые данные в следующие ячейки:
начальная скорость тела-С7
угол (в градусах) -С8
ускорение свободного падения-С9
конечный момент времени - в С12.
Начальный момент времени (ячейка С11) принимается равным нулю
В ячейку С13 ввести формулу, позволяющую рассчитать
интервал времени At = ———: =(С12-С11)/20
n
Здесь число 20 означает количество интервалов п, на которое разбивается
5
выбранный промежуток времени tmin ^ tmax. Таким образом, наша таблица будет содержать n+1 = 21 точек.
|
 Скачать 5.79 Mb.
Скачать 5.79 Mb.
