Практическая работа. Информационные ресурсы общества. Образовательные информационные ресурсы. Работа с программным обеспечением

• Название: Информационные ресурсы общества. Образовательные информационные ресурсы. Работа с программным обеспечением
• Дата: 06.12.2022
• Размер: 5.79 Mb.
• Имя файла: Практическая работа.doc
• Тип: Практическая работа; #830229
• страница: 25 из 44

Г руппа Символы

Группа Символы содержит основные математические символы, греческие буквы, операторы, на рисунке раскрыта строка Основные математические символы:


Осмоомыt математические симоола ^

V Оснос-шс мэтемати-иски: симболы

Греческие б/кзв Ьуевэподобные симболы Операторы Стрелки

Отношения с отрицанием Особые начертания букв Геометрия

И

е д

ИНЗИ0НИ JJ

00000Н

Рисунок 4. Меню группы Символы, строка Основные математические символы

Г руппа Структуры

Группа Структуры содержит шаблоны Дробь, Индекс, Радикал и др. Раскроем шаблон Дробь:



КII Скоб ко *

•о» функция *

;} диакрмтиче

Простая дробь



Обычная г роста* дробь



Я

г

Прямоугольники — это местозаполнители, в которые следует внести требуемый символ или вложить другой шаблон.

Набор формулы

Создадим небольшую формулу для вычисления расстояния между двумя точками:

d = л/('Ч - ^хг )^{2 +} СУж - У г У

Порядок команд:

• 
  Выбрать вкладку Вставка, в группе Символы выбрать строку Формула. Откроется панель Конструктор, Работа с формулами.
  
• 
  Набрать с клавиатуры букву d и знак “=”.
  
• 
  Раскрыть группу Радикал, выбрать шаблон Квадратный корень.
  

{О} Скобка *

*■* Функция *

Hi

Дробь Индекс'Радикал Интеграл крупный .. .

- оператор- & Диакритические знаки - Ц

Радикалы

Vi-J

I Квадратный корень I



Обычные радикалы



Рисунок 6. Группа Радикал

• 
  Выделить заполнитель, выбрать группу Скобка, выбрать круглые скобки.
  
• 
  Щелкнуть на местозаполнителе, квадратик будет выделен.
  
• 
  В группе Индекс выбрать шаблон Нижний индекс, местозаполнители шаблона появятся в формуле, внести символ x и нижний индекс 1 в соответствующие поля.
  
• 
  Щелкнуть по шаблону, чтобы он был выделен, поставить знак минус.
  
• 
  Аналогично внести символ x и нижний индекс 2.
  
• 
  Щелкнуть по шаблону скобки, он будет выделен, тогда выбрать шаблон верхний индекс, заполнить верхнее поле символом 2.
  
• 
  Выделить все подкоренное выражение, поставить символ плюс.
  
• 
  Аналогично набрать второе слагаемое.
  

Ход работы:

1. 
   Изучить теоретическое обоснование.
   
2. 
   Выполнить практические задания.
   
3. 
   Оформить отчет.
   

Практические задания:

Задание №1. Составить конспект по учебнику И. И. Сергеева (стр. 167-170), (§6.7). Задание №2.

С помощью формульного редактора Equation Editor наберите формулу:


?, (^1

Методические указания по выполнению задания 2.

• 
  Вызовите формульный редактор;
  
• 
  В палитре шаблонов выберите шаблон с индексами;
  
• 
  Наберите греческое "Хи"
  
• 
  Обратите внимание на различный вид курсоров. Вводимый символ вставляется в позицию, определяемую вертикальной чертой курсора!
  
• 
  Подведите курсор в поле верхнего индекса и нажмите 2;
  
• 
  Введите "=" после Х;
  
• 
  — из палитры шаблонов выберите знак суммы с верхним и нижним индексами, и введите индексы;
  
• 
  Выберите из палитры шаблонов объект с верхним индексом
  
• 
  Выберите шаблон со скобками;
  
• 
  Выберите шаблон для дроби;
  
• 
  — Выберите шаблон с нижним индексом, введите Хи, переведите курсор в следующую позицию (стрелкой -> или шелчком мыши), наберите "-", затем "m"
  
• 
  В знаменателе введите "а"
  
• 
  В месте верхнего индекса наберите 2;
  
• 
  Выйдите из редактора формул, щёлкнув левой кнопкой мыши вне поля редактирования.
  

Задание 3. Наберите

систему неравенств

5 + д/25 - 4p
² Р

5 -yl25 - 4p
² Р

< 0, > 0.

Задание 4. Наберите формулу вычисления корней квадратного уравнения

x

- b ± Vb¹ - 4ac

1,2

2a

Место для уравнения.

Задание 5. Наберите формулу предела

a) lim

ln cos x

^x^⁰ ln cos 3 x

x² - 2x +1 ^{, b)} hm 2 ^, c) lim

sin x

^x^° x -1

.d)lim

1 - cosx

1 Л.1Л.Л.Л. f

⁰ cos x - 1 ^x^° x( 1 + x -1)

Задание 6. Наберите формулу интеграла

^{1 a)} J ^arctgxdx ^{, b)} ^3 _x4 , C) J cos x cos 5 xdx .

x


Контрольные вопросы:

1. 
   Как осуществить запуск редактора формул, выход из редактора формул и последующее редактирование формулы?
   
2. 
   Расскажите порядок создания математических формул. Ввод специальных математических символов.
   
3. 
   Какие вы знаете основные параметры редактора формул?
   

Содержание отчета:

1. 
   Тему, цель работы.
   
2. 
   Ответы на контрольные вопросы по указанию преподавателя.
   
3. 
   Заключение (выводы).
   

Литература.

Основные источники (ОИ):

Таблица 2б

Номер п/п	Автор	Наименование	Издательство, год издания
ОИ1	И. И. Сергеева	Информатика Режим доступа: http: //znanium .com/ bookread2 .php?id=517652	НИЦ ИНФРА-М, 2016
ОИ2	М. С. Цветкова	Информатика. [Текст]: Учебное пособие для студ. учреждений среднего профессионального образования	М.: Академия, 2017

Дополнительные источники (ДИ):

Таблица 2в

№ п/п	Автор	Наименование	Издательство, год издания
ДИ 1	В. Д. Колдаев	Сборник задач и упражнений по информатике Режим доступа: http: //znanium. com/ bookread2 .php?id=504814	ИНФРА-М, 2015
ДИ 2	Е. А. Колмыкова	Информатика. [Текст]: Учебное пособие для студ. учреждений среднего профессионального образования	М.: Академия, 2014
ДИ 3	Н. Г. Плотникова	Информатика и информационно­коммуникационные технологии (ИКТ) Режим доступа:	ИНФРА-М, 2014

		http: //znanium .com/ bookread2.php?id=433676
ДИ4	Р. Ю Царев	Программные и аппаратные средства информатики Режим доступа: http://znanium.com/ bookread2 .php?id=550017	Краснояр.: СФУ, 2015

Практическая работа №24

Тема: Ввод математических формул и вычисления по ним.

Цели: приобрести навыки работы в EXCEL, научиться создавать вычислительные таблицы, выполнять расчеты с использованием абсолютных ссылок.

Студент должен знать:

-I- назначение и возможности электронных таблиц;

-I- основные объекты окна программы Excel; уметь:

-1- проводить различные вычисления с использованием мощного аппарата формул.

Теоретическое обоснование.

1. 
   Математические формулы и ссылки в Excel
   

Обработка хранимых в ячейках рабочих листов Excel, осуществляется по
формулам, определенным пользователем. Для перехода в режим создания формул
необходимо выделить ячейку и ввести знак =

В формулах могут использоваться как стандартные арифметические операции,
так и встроенные функции Excel.

При вычислении математических выражений по формуле Excel
руководствуются следующими традиционными правилами, определяющими
приоритет выполнения операций:

• 
  в первую очередь вычисляются выражения внутри круглых скобок;
  
• 
  определяются значения, возвращаемые встроенными функциями;
  
• 
  выполняются операции возведения в степень(^Л), затем умножения (*) и
  деления(/), а после - сложения (+) и вычитания (-).
  

Необходимо отметить, что операции с одинаковым приоритетом выполняются
слева направо.

В Excel предусмотрен контроль за вводом формул: при несоответствии
количества открывающих и закрывающих скобок выводится сообщение (рисунок

2):



Рисунок 2-Сообщение об ошибке.

Ошибочное значение- это результат формулы, которую Excel не может вычислить. В Excel определены семь ошибочных значений.


Таблица 1-Описание ошибок

Ошибочное значение	Описание
#ДЕЛ/0!	Попытка деления на ноль. ошибка обычно связана со ссылкой делителя на пустую ячейку.
#ИМЯ?	В формуле используется имя, отсутствующее в списке имен окна диалога Присвоение имени.
#ЗНАЧ!	Введена математическая формула, которая ссылается на текстовое значение.
#ССЫЛКА!	Отсутствует диапазон ячеек, на которые ссылается формула
#Н/Д	Нет данных для вычислений
#ЧИСЛО!	Задан неправильный аргумент функции.
#ПУСТО!	В формуле указано пересечение диапазонов, но эти диапазоны не имеют общих ячеек

Функции в Excel. Арифметические и тригонометрические функции.

В Excel имеется целый ряд встроенных математических функций, существенно облегчающих решение задач.

В качестве аргумента могут использоваться как не посредственное значение, так и идентификатор ячейки.

При использовании в функции нескольких аргументов они отделяются одним от другого точкой с запятой.

На пример, формула =ПРОИЗВЕД(А1;В2;С4) указывает Excel, что необходимо перемножить числа в ячейках А1, В2, С4.

Однако любой аргумент может быть диапазоном, содержащим произвольное число ячеек лист.

На пример, формула =ПРОИЗВЕД(А1:А2; В2:В4)имеет два аргумента, но перемножает содержимое шести ячеек.

Некоторые функции, например Пи(), не имеют аргументов.

Комбинацию функций можно использовать для создания выражения, например

=СУММ(КОРЕНЬ(16);СО$(А1*ПИ()))

Перечень встроенных математических функций из категории Арифметические и тригонометрические.

Таблица 2-Основные математические функции.

ФУНКЦИЯ	ОПИСАНИЕ
Функция ABS()	Возвращает модуль (абсолютную величину) числа.
Функция ACOS()	Возвращает арккосинус числа.
Функция ASIN() Функция ATAN() Функция COS() Функция ГРАДУСЫ() Функция EXP()	Возвращает арксинус числа. Возвращает арктангенс числа. Возвращает косинус числа. Преобразует радианы в градусы. Возвращает число e, возведенное в указанную степень.
Функция LN()	Возвращает натуральный логарифм числа.
Функция LOG()	Возвращает логарифм числа по заданному основанию.
Функция LOG10()	Возвращает десятичный логарифм числа.

Функция ПИ()	Возвращает число пи.
Функция СТЕПЕНЬ()	Возвращает результат возведения числа в степень.
Функция ПРОИЗВЕД()	Возвращает произведение аргументов.
Функция РАДИАНЫ()	Преобразует градусы в радианы.
Функция SIN() Функция КОРЕНЬ()	Возвращает синус заданного угла. Возвращает положительное значение квадратного корня.
Функция СУММ()	Суммирует аргументы.
Функция СУММЕСЛИ() Функция TAN()	Суммирует ячейки, удовлетворяющие заданному условию. Возвращает тангенс числа.

Ввод функций

Функции могут вводится в рабочий лист несколькими способами. После ввода знака = функция либо может быть введена непосредственно с клавиатуры, либо выбираться в поле имени, которое в этой ситуации становиться полем функции.

Существует также два способа, равноценных последнему, но не требующих предварительного ввода знака равенства:

4- через пункт меню Вставка-Функция;

4- с помощью кнопки Вставка функции —

Функция определяется за два шага. На первом шаге в открывшемся окне диалога Мастер функций необходимо сначала выбрать категорию в списке Категории, а затем в алфавитном списке Функция выделить необходимую



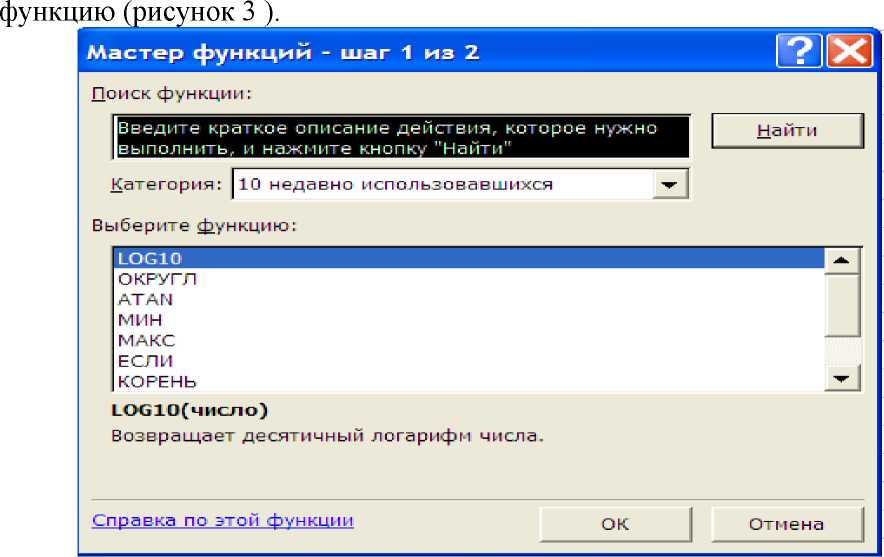
Рисунок 3- Первый шаг Мастера Функций

На втором шаге задаются аргументы функции. Второе окно диалога Мастера функций содержит по одному полю для каждого аргумента выбранной функции. Если функция имеет переменное число аргументов, то окно диалога увеличивается при воде дополнительных аргументов. После задания аргументов необходимо нажать кнопку ОК или клавишу Enter.Пример на рисунке 4



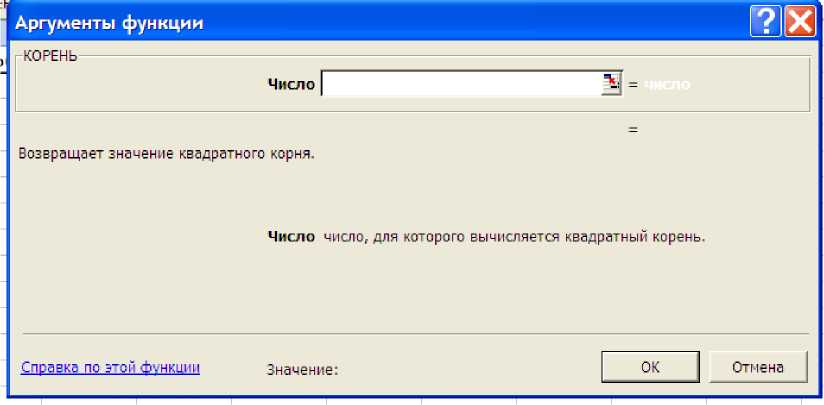
Рисунок 4 Второй шаг Мастера Функции

Ход работы.

1. 
   Изучить теоретическое обоснование.
   
2. 
   Составить таблицу значений функции
   
3. 
   Оформить отчет
   

Практические задания.

Задание №1. Составить конспект по учебнику И. И. Сергеева стр. 180-183 (§7.1­7.2)

Задание №2. Используя возможности табличного процессора Exсel решить квадратное уравнение:

Вариант	Условие задания
1	х2+5х-6=0
2	2х2-3х+1=0
3	2х2-3х+4=0
4	9х2+6х+1=0
5	х2-10х+24=0
6	х2-9х+8=0
7	х2+х-6=0
8	4х2-17х+4=0
9	9х2+77х-36=0
10	2х2-9х-5=0
11	6х2-5х-1=0
12	х2+7х+12=0
13	х2-2х-35=0
14	2х2-5х-3=0
15	3х2-8х+5=0

Задание №3. Используя возможности табличного процессора Excel решить прикладную задачу:

Номер

варианта

Исходные данные

Функция

1

Х=1,426, У=-1,220, Z=3,5

2cos( х _²

а = ^ ⁶⁾, b= 1 + —

1 . 2 ’ " ' 2 ’

—hsin y z

² 3 h

5

2

X=1,825, Y=18,225,

Z=-3,298


a =

^х'-³ё

y-

, ^b = ⁽y - x)

(y - <sup>x)

1</sup> + ⁽y ^{- x)2}

X=-0,5, Y=1,7, Z=0,44

а =

sin( xz + y)

2e

1-x

, b = e sin(xz² cos 2z) -1

4

a=1,5, b=15,5, x=0,5

I 2 T b² sin(x + а) ₂

w = V x + b ¹ , y = cos x-

x

Va² +b²

a=16,5, b=3,4, x=0,61

^ = x ³tg ²( x + b) +

а

yjx + b

Q

bx² -a

e^a -1

6

a=0,7, b=0,05, x=0,5

^ =

— + cos² (x + b), R = ^{x (X +1)} - sin² (x + a) a b

7

a=1,1, b=0,004, x=0,2

y = sin³(x² + a) -

x x , „3

— , z = h cos( x + b)

a

m=2, c=-1, t=1,2, b=0,7

^f = ^mtg^(t) + \^c sⁱⁿ ^, z = m cos(bt sin t) + c

9

a=3,2,

b=17,5,

x=-4.8

7 ₂ a . ia ,bx_s

y = btg x 2—, d = ae cos(—)

sin² x a

10

a=10,2, b=9,2, x=2,2

f = ln(a + x ) + sin²1 — 1, z =

x