Контрольная Информационные технологии. Информационные технологии

Название	Информационные технологии
Анкор	Контрольная Информационные технологии
Дата	10.06.2021
Размер	1.51 Mb.
Формат файла
Имя файла	Контрольная Информационные технологии.docx
Тип	Документы #216518
страница	6 из 7

1 2 3 4 5 6 7

ИНТЕРПОЛЯЦИЯ. ЛИНЕЙНЫЕ И НЕЛИНЕЙНЫЕ УРАВНЕНИЯ И СИСТЕМЫ. МИНИМИЗАЦИЯ ФУНКЦИИ

Цель работы: рассмотреть основные функции, предоставляемые системой MATLAB для интерполяции данных, а также решения систем линейных и нелинейных уравнений, поиска точек экстремумов функций.

Теоретическая часть

Рассмотрим некоторые функции, предоставляемые системой MATLAB для решения задач, часто встречающихся на практике.

Интерполяция

Предположим, что в результате эксперимента или реализации численного метода была получена зависимость между величинами x и y в табличной форме. При этом часто для анализа полученных результатов необходимо иметь аналитическую зависимость y=f(x). Задача интерполяции состоит в построении аналитической зависимости в некотором смысле приближающей полученные табличные данные.

Для аппроксимации может быть выбран полином степени n – 1 (n – количество наблюдений)

Коэффициенты p_m полинома (1), проходящего через заданные табличные узлы [x_i, y_i], могут быть найдены с помощью функции vander, которая создает матрицу Вандермонда. (см. пример 1).

Пример 1:

>> x= [0.05; 0.1; 0.17; 0.25; 0.3; 0.36];

>> y= [0.05; 0.1003; 0.1717; 0.2553; 0.3093; 0.3764];

>> P = vander(x)\y

P=

– 4.5785

5.0346

– 1.6381

0.3434

0.9746

0.0006

Вектор P содержит значения коэффициентов p_m полинома y(x). Можно выбрать полином, который дает наименьшее среднеквадратическое уклонение в узлах с помощью функции polyfit:

P= polyfit(x,y,N); % N – степень полинома.

Для вычисления значения полинома в любой точке отрезка [x₁; x_n], можно использовать функцию polyval: y=polyval(P,x).

На практике широкое распространение получила аппроксимация сплайнами. Сплайн интерполяция осуществляется с помощью функциций spline и pchip, обращение к которым может иметь вид:

ys = spline (x, y, xs) ys = spline(x, y)

ys = pchip (x, y, xs) ys = pchip(x, y)

В первом случае в переменную ys будет возвращено значение в точке xs, полученное путем, сплайн интерполяции на содержащем данную точку отрезке. Во втором случае будет возвращена кусочно-полиномиальная форма – таблица содержащая каждый интервал и значения коэффициентов кубического полинома, использованного для интерполяции на данном отрезке (рисунок 26).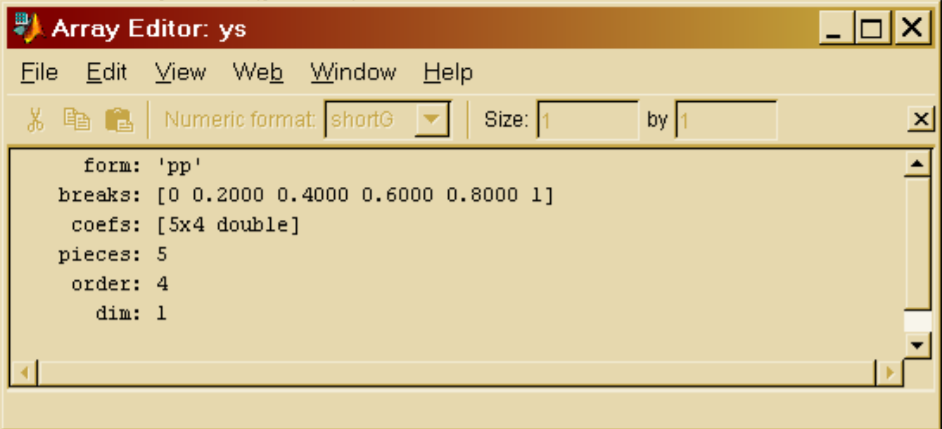

Рисунок 27. – Кусочно-полиномиальная форма
Доступ к значению коэффициентов можно получить следующим образом:

>> x=-3:3;

>> y= [–1 –1 –1 0 1 1 1];

>> ys= spline (x, y);

>> koef= ys.coefs

koef=

0.2500 -0.7500 0.5000 -1.0000

0.2500 0 -0.2500 -1.0000

-0.2500 0.7500 0.5000 -1.0000

-0.2500 0 1.2500 0

0.2500 -0.7500 0.5000 1.0000

0.2500 0.0000 -0.2500 1.0000

В переменную koef будет помещена матрица коэффициентов (первый столбец соответствует 3 – ей степени и т.д.) строки которой соответствуют заданным интервалам. Получить значение функции в точке по полученной кусочно – полиномиальной форме можно с помощью функции ppval: y=ppval (xs, ys), где ys – кусочно – полиномиальная форма, а xs – точка в которой неодходимо вычислить функцию.

Приведем пример работы функций spline и pchip (рисунок 27):

function Prog

x=-3:3;

y= [-1 -1 -1 0 1 1 1];

t= [-3.5:0.05:3.5];

ps = spline (x, y);

pp= pchip (x, y);

plot (x, y, 'ko', t, ppval (ps, t), 'k:', t, ppval (pp, t), 'k-');

legend ('(x, y)','spline','pchip',2);

title ('Spline Pchip');

xlabel('x'); ylabel('y');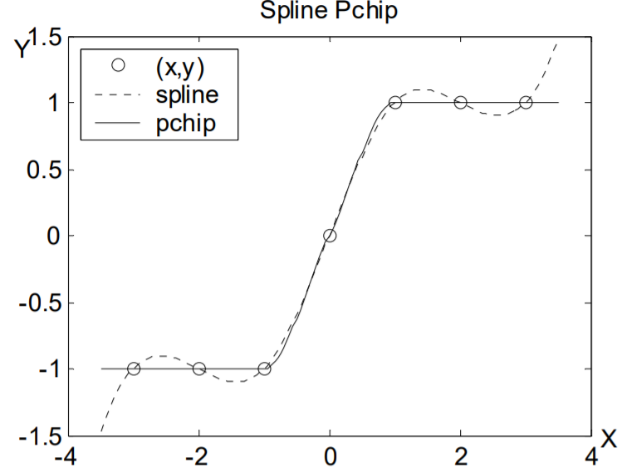

Рисунок 28. – Функции spline и pchip
Для интерполяции отрезками прямых можно воспользоваться функцией interp1: ys=interp1(x, y, xs);

x, y – узлы интерполяции, xs – обсциссы контрольныхточек в которых вычисляется значение табличной функции.

Нелинейные уравнения

Для решения нелинейных уравнений вида f(x)=0 используется функция fzero. Алгоритм реализованный ею представляет собой комбинацию хорошо известного метода бисекции, метода секущих и метода обратной квадратичной интерполяции. Обращение к функции в простейшем случае выглядит следующим образом:

x= fzero (fun, x0)
Аргумент fun представляет собой функцию f(x), которая может быть задана как:

Формула с неизвестным x, заключенная в одинарные кавычки.
Имя m – файла в одинарных кавычках и без расширения m.
Указатель на функцию.

Указатель на функцию создается с помощью значка @, и представляет в системе отдельный тип данных (function handle). Так, например, если имя функции funcs (или имеется отдельный файл funcs.m), то указатель на эту функцию создается следующим образом:

>> h=@funcs.

И обращение к функции fzero будет выглядеть так:

>> x=fzero (h, x₀); % возможна прямая запись x=fzero (@funcs, x₀);

Аргумент x₀ может быть задан одним из двух способов:

Как вектор [a b] представляющий интервал (a
Как скалярное значение, окрестности которого предполагается нахождение корня.

Чтобы облегчить работу по выбору начального приближения, разумнее всего построить график функции

Приведем пример решения уравнения нелинейного уравнения

x∙ e^-x+ sin(x):

>> x=0:0.1:2*pi;

>> plot (x, x.*exp(-x) +sin(x),' k ');

>> grid on

>> title('y=x*exp(-x) +sin(x)');

>> xlabel (' x ');

>> ylabel (' y ');

Из графика (рисунок 28) видно, что один корне находится на интервале [3, 4]. И этой информацией естественно воспользоваться при обращении к функции fzero:

>> x = fzero (' x.*exp(-x) +sin(x)', [3 4])

x = 3.2665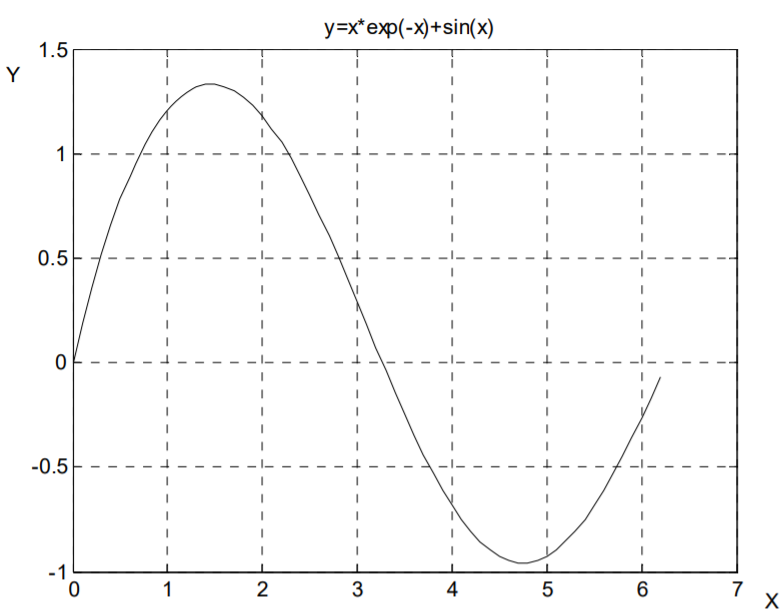

Рисунок 29. – График функции
Если бы уравнение было сохранено в виде m – файла с именем F1.m,

function y=F1(x)

y= x*exp(-x) +sin(x);

то обращение к функции fzero могло бы иметь вид

>> x= fzero (@F1, x0)

x = 3.2665.
Решение систем линейных и нелинейных уравнений

В силу специфики системы MATLAB решение совместной системы линейных уравнений может быть осуществлено с помощью левого матричного деления:

>> y=A\b;

где x- вектор неизвестных, b- вектор свободных членов системы, А- матрица коэффициентов системы.

Для решения системы можно воспользоваться функцией, возвращающей обратную матрицу – inv(A), тогда решение может быть представлено следующим образом:

>> x=inv(A)*b;

Для определения совместности имеющейся системы можно вычислить определитель матрицы А, воспользовавшись функцией det(A).

Если система является несовместной, то можно воспользоваться псевдорешением. Тогда в качестве решения будет получен вектор x, который при подстановке в исходную систему дает вектор невязки (R=A*x – b) минимальный по евклидовой норме (метод наименьших квадратов). Очевидно, что для совместной системы псевдорешение является обычным решением. Псевдорешение ищется следующим образом:

>> x=pinv(A)*b;

Пример:

>> a= [3 9;4 12]

a=

3 9

4 12

>> b= [1;2];

>> det(a) % Как видно главный определитель системы равен 0 ans=0 Получим псевдорешение системы:

>> x=pinv(a)*b

x = 0.0440 0.1320

В общем виде систему нелинейных уравнений можно записать в виде F(x)=0, где x – вектор неизвестных системы. Для решения систем нелинейных уравнений предназначена функция fsolve. Алгоритм ее работы использует начальное приближение x0 и базируется на минимизации суммы квадратов компонент функции F методами Гаусса – Ньютона и Левенберга – Марквардта. В простейшем случае обращение к функции fsolve имеет вид:

x=fsolve (F, x0);

Подпрограмма должна быть оформлена следующим образом: function y=Sistema(x) y=[x(1)+ x(2) – sin(pi*x(1)); x(1) – x(2) – cos(pi*x(2))]; Обращение к функции fsolve будет выглядеть следующим образом: >> x0=[1 2]; >> x=fsolve(@Sistema,x0)

x = 0.3915 0.5510
Поиск минимума функции одной переменной

Для поиска минимума функции f(x) на отрезке [a, b] можно воспользоваться функцией fminbnd:

>> x=fminbnd(F, a, b);

Если минимизируемая функция на заданном отрезке многоэкстремальна, то fminbnd наидет какой-либо один минимум и не выдаст никакой информации о других. Поэтому рекомендуется перед использованием fminbnd построить график.

В заключение теоретического введения отметим, что все рассмотренные выше функции, предлагаемые системой MATLAB допускают и другие формы обращения к ним (нами приведены простейшие формы), позволяющие получить более полную информацию о процессе вычислений. Для получения сведений о возможных формах обращения к функциям системы, можно получить используя команду help:

>> help Fun

Fun – имя интересующей функции (например help fsolve).
2. Рабочее задание.

1. Выполнить упражнения из описания лабораторной работы.

2. Оформить результаты выполнения, иллюстрируя скриншотами.

3. Сделать вывод о проделанной работе.

Ход выполнения работы.

При заданном значении давления зависимость плотности вещества от температуры задана таблично (таблица 1):

Таблица 5

T, K	20	40	70	90	100	150	200	250
P, кг/м³	80	63,4	35,3	26	23	15,2	11,4	9,2

Определить значения плотности при температуре T0= 30, 50, 60, 80, 93, 135, 178, 223 K

Получить плотность при указанных температурах можно воспользовавшись интерполяцией исходной табличной функции ρ(T).

Интерполяцию осуществим разными методами – кубическими сплайнами spline и линейно (Linear):

>> T= [20 40 70 90 100 150 200 250];

>> T0= [30 50 60 80 93 135 178 223];

>> Ro= [80 63.4 35.3 26 23 15.2 11.4 9.2];

Определим значения плотности при температуре T0 с помощью интерполяции сплайнами:

>> RoSpline=spline (T, Ro);

>> RoTs = ppval (T0, RoSpline); % значения плотности при темпT0

Построим график RoSpline(T) (рис.29):

>> t=20:0.5:250;

>> plot (t, ppval (t, RoSpline),' k ');

Значения плотности с помощью линейной интерполяции получим следующим образом:

>> RoTL=interp1(T, Ro, T0);

Поcтроим график (рис. 4):

>> hold on;

>> plot (t, interp1(T, Ro, t),'k--');

>> title (' Spline & Linear ');

>> legend (' Spline ', ' Linear ');

>> xlabel('T');

>> ylabel('Ro');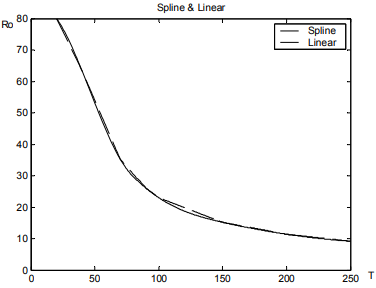

Рисунок 30. – График RoSpline(T)
Как видно разный способ интерполяции дает разный результат вне табличных узлов. Оценим среднеквадратические ошибки использованных методов интерполяции если предположить, что были проведены дополнительные эксперименты, из которых определено (Таблица 6):

Таблица 6

T, K	30	50	60	80
P, кг/м³	72,7	52,8	42,9	30

>> Td = [30 50 60 80];

>> Rod = [72,7 52.8 42.9 30].

Определим значение плотности при температуре Td:

>> RoTds = ppval (Td, RoSpline); % кубическими сплайнами

>> RoTdL= interp1(T, Ro, Td); % линейная интерполяция

Оценим погрешность работы примененных интерполяционных методов:

>> ZSp = 100*sqrt ((RoTds– Rod). ^2). /Rod;

>> ZLin= 100*sqrt ((RoTdL– Rod). ^2). /Rod;
1.Определить минимум функции

на отрезке x= [1, 5], и получить решение уравнения y(x)=0.

Построим график функции y(x) на заданном отрезке (рис.5):

>> x=1:0.1:5

>> plot (x, cos(pi*x./5)-sin(pi*x). /x);

>> title (' y=cos(pi*x/5)-sin(pi*x)/x ');

>> xlabel (' x ');

>> ylabel (' y ');

Как видно из рис. 30 функция y(x) имеет на заданном отрезке два локальных минимума: первый на отрезке [2,3], второй – [4,5]. Для их определения воспользуемся функцией fminbnd:

>> x (1) =fminbnd (' cos(pi*x./5)-sin(pi*x). /x ',2,3);

>> x (2) =fminbnd (' cos(pi*x./5)-sin(pi*x). /x ',4,5); Для решения уравнения y(x)=0 воспользуемся функцией fzero:

Как видно из графика, решение находится в окрестности точки x=2

>> x=fzero (' cos(pi*x./5)-sin(pi*x). /x ', 2);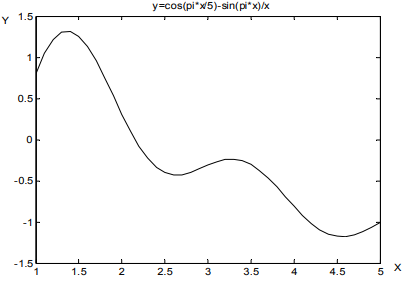

Рисунок 31. – График функции y(x)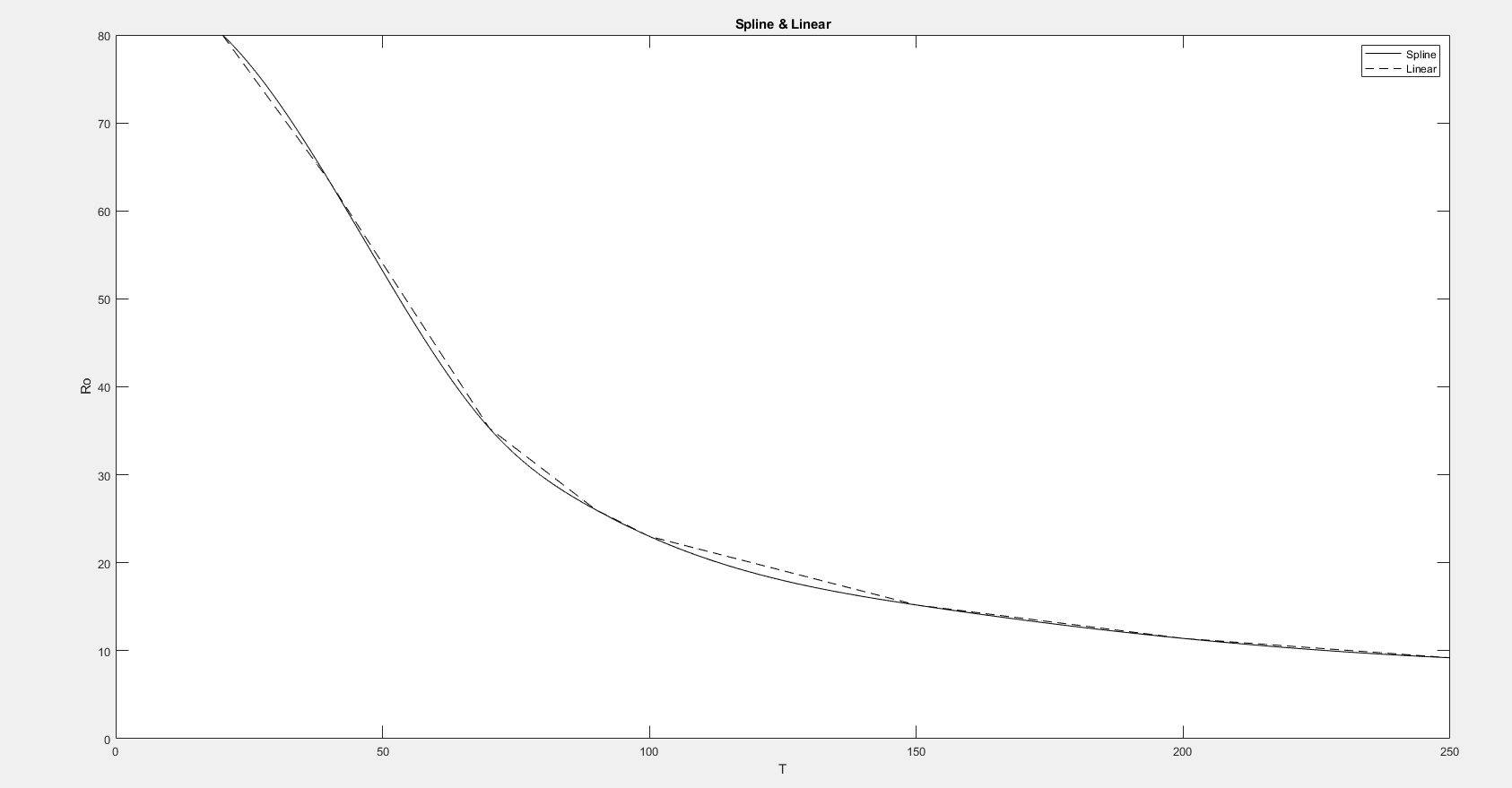

Рисунок 32. – Полученный график RoSpline(T)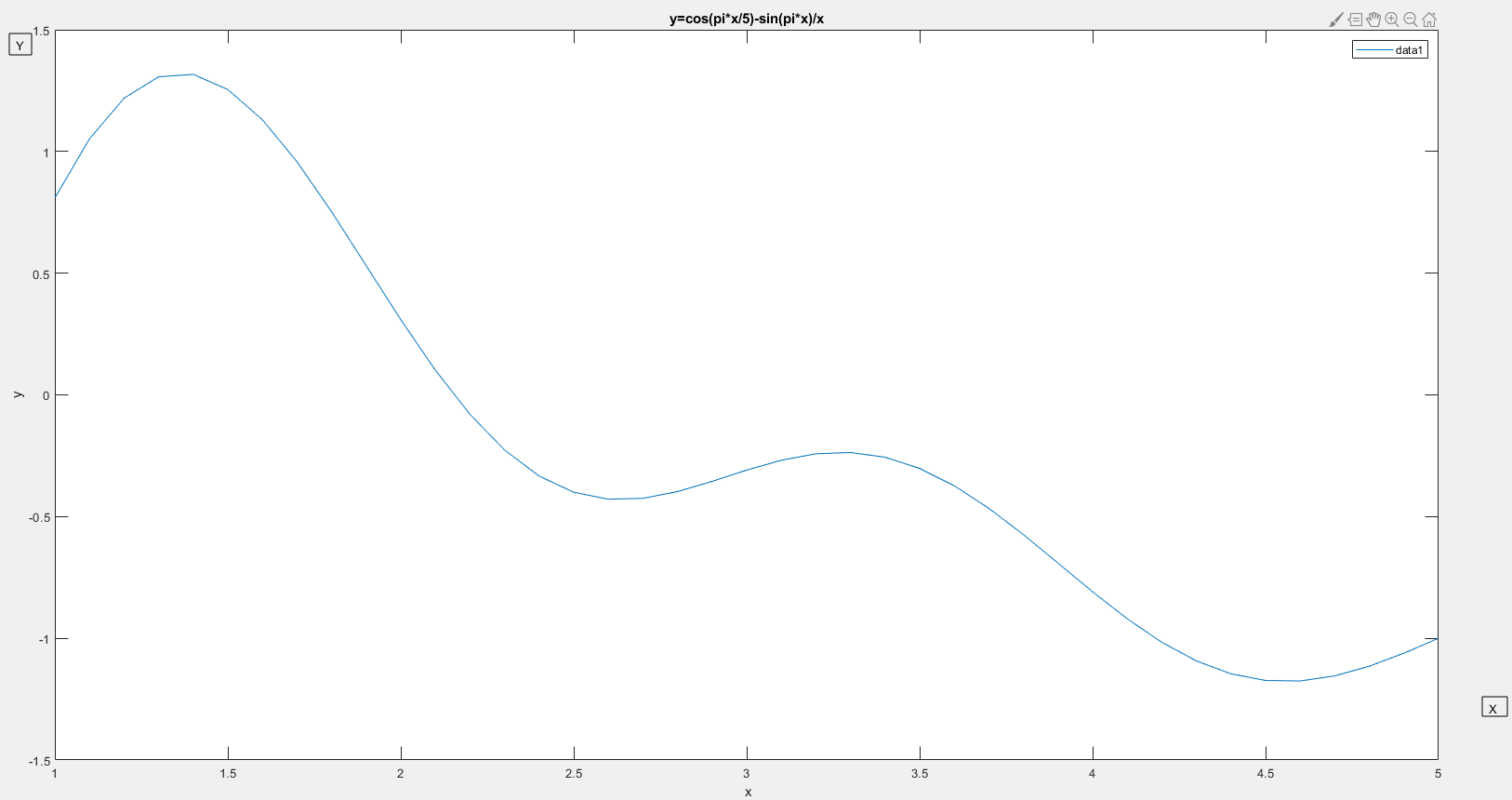

Рисунок 33. – Полученный график функции
Вывод: Мы рассмотрели основные функции, предоставляемые системой MATLAB для интерполяции данных, а также решения систем линейных и нелинейных уравнений, поиска точек экстремумов функций.

1 2 3 4 5 6 7