Контрольная Информационные технологии. Информационные технологии
 Скачать 1.51 Mb. Скачать 1.51 Mb.
|
Визуализация в MATLABЦель работы: получение навыков визуализации решения задач в системе MATLAB. В практической части лабораторной работы необходимо построить графическую интерпретацию решения задачи об определении электрического поля, порождаемого двумя электрическими зарядами. Теоретическая часть Одно из достоинств системы MATLAB – обилие средств графики, начиная от команд построения простых графиков функций одной переменной в декартовой системе координат и кончая комбинированными и презентационными графиками с элементами анимации, а также средствами проектирования графического пользовательского интерфейса (GUI). Особое внимание в системе уделено трехмерной графике с функциональной окраской отображаемых фигур и имитацией различных световых эффектов. Рассмотрим примеры наиболее часто используемых средств визуализации системы. Функции одной переменной у(х) находят широкое применение в практике математических и других расчетов, а также в технике компьютерного математического моделирования. Для отображения таких функций используются графики в декартовой (прямоугольной) системе координат. При этом обычно строятся две оси – горизонтальная X и вертикальная Y, и задаются координаты х и у, определяющие узловые точки функции у(х). Эти точки соединяются друг с другом отрезками прямых, т. е. при построении графика осуществляется линейная интерполяция для промежуточных точек. Поскольку MATLAB – матричная система, совокупность точек у(х) задается векторами X и Y одинакового размера. Для построения таких графиков используется процедура fplot, на пример: >>x= [0:0.1:6.28]; >>y=sin(x). *0.5; >>plot(x,y); Результатом выполнения будет график функции y(x)=0.5sin(x) Если обратится к процедуре plot повторно, то она создаст новое окно с заголовком Figure No.2 и разместит в нем следующий график. Совместить оба графика в одном окне можно двумя разными способами. В первом случае перед вызовом процедуры plot мы должны построить таблицы обеих функций, например, (x1, y1) и (x2, y2), и обратится к процедуре следующим образом (результат на рисунке 14): >>x1= [0:0.1:6.28]; >>y1= sin(x1). *0.5; >>y2=cos(x1). *0.5; >>plot(x1, y1,x1,y2); Второй способ заключается в блокировании режима создания нового графического окна с помощью процедуры hold on. Так, например, предыдущий результат можно получить так: >>plot (x1, y1); >>hold on; >>plot (x1, y2); 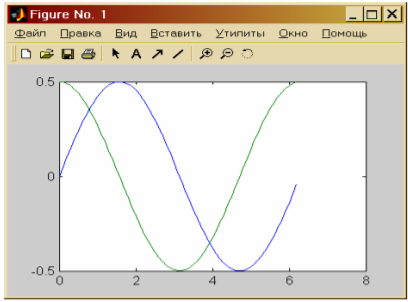 Рисунок14. – График Figure Заметим, что график второй функции отображен другим цветом. Повлиять на выбор цвета графика может пользователь, указав в процедуре дополнительный третий параметр: >>plot(x,y,'g') В данном случае выводимый график будет зеленого цвета (синий по умолчанию). Дополнительно предусмотрена возможность задания типа линии и маркера, которые указываются вместе с цветом. Дополнительно можно снабдить график заголовком (процедура title), подписать оси (процедуры xlabel,ylabel), нанести координатную сетку (процедура grid on) и разместить легенду (процедура legend). Используем все эти возможности для рисунка 14 (рисунок 15): >>x1= [0:0.2:6.28]; >>y1= sin(x1).*0.5; >>y2=cos(x1).*0.5; >>plot(x1,y1,'k–s',x1,y2,'b--o'); % k – черный, '–' сплошная, 's' – маркер квадратный. >>legend('sin', 'cos',4); >>ylabel('y'); >>xlabel('x'); >>grid on; >>title('Function sin & cos'); В процедуре legend третий параметр указывает место расположения легенды: -1 – легенда помещается вне поля графика, вверху справа. 0 – система выбирает лучшее место в поле графика не перекрываемое данными. 1,2,3,4 – по углам в поле графика. 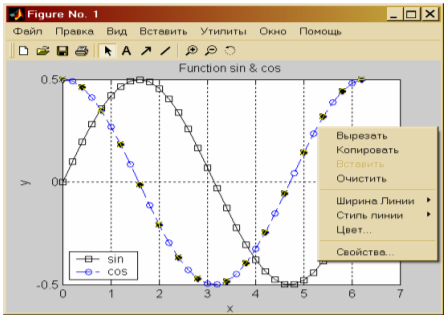 Рисунок 15. – Дополнительные возможности Редактирование графика можно производить непосредственно из окна Figure. Для этого следует выбрать в строке меню окна стрелку, затем выбрав необходимый для редактирования график, с помощью правой кнопки мыши открыть меню (рисунок 16), используя которое можно установить нужный цвет, маркер, стиль линии и т.д. Пункт “вставить” (Insert) главного меню окна можно использовать для создания легенды, заголовка, поясняющих надписей в поле графика и т.д. Для корректировки свойств осей (масштаба и т.д.) необходимо использовать пункт “правка”→”свойства осей”(Edit→Axes properties). На практике большое распространение получили функции двух переменных, графическим изображением которых является трехмерная поверхность. В MATLAB такие поверхности должны быть заданы узлами сетки размерности m× n, заполняющей на плоскости Oxy прямоугольную область, и массивом той же размерности, представляющим значения функции в узлах этой сетки. Для формирования равномерной прямоугольной сетки удобно воспользоваться функцией meshgrid: >> x= [0 1 2 3 4 5]; >> y= [0 2 4]; >> [X, Y] =meshgrid(x,y) Для отображения поверхности используются две основные функции- mesh и surf. Первая строит проволочный каркас поверхности, вторая- закрашенную поверхность. Приведем пример построения поверхности заданной равномерной сеткой с шагом 0,25 и функцией Z (x, y) = x∙ exp (-x2- y2) (рисунок 4): >> [X,Y]= meshgrid([-2:0.25:2]); >> Z=X.* exp(– X .^2 – Y.^2); >>mesh (X, Y, Z); >>XLabel('X'),YLabel('Y'),ZLabel('Z'); 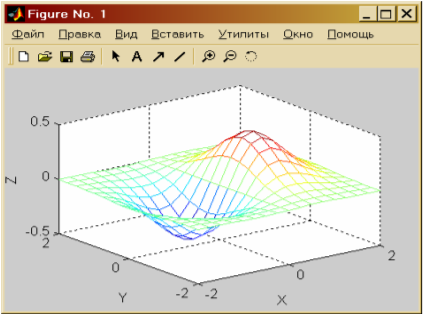 Рисунок 16. – Редактирование графика Закрашивание каждой чешуйки поверхности осуществляется функциями surf и surfc. Используя предыдущую сетку и функцию обратимся к функции surf (рисунок 17): >> surf(x,y,Z); >> XLabel('X'), YLabel('Y'), ZLabel('Z'); 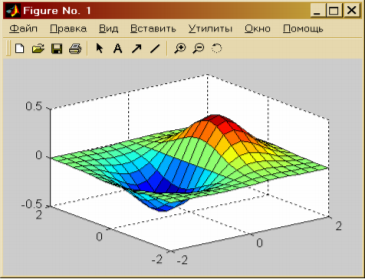 Рисунок 17– Построение поверхности заданной равномерной сеткой с шагом 0.25 Рабочее задание 1. Выполнить упражнения из описания лабораторной работы. 2. Оформить результаты выполнения, иллюстрируя скриншотами. 3. Сделать вывод о проделанной работе. Ход выполнения работы. Реализация приведенного алгоритма в MATLAB будет выглядеть следующим образом: 1. Ввод исходных данных (рисунок 18): >> x1= –5; >> x2=5; >> q=1e-9; >> E0=8.85e-12; >> C=1/(4*pi*E0); 2. Формирование сетки >> x0=[–0.7:0.1:0.7]; >> y0=[–0.7:0.1:0.7]; >> [x,y]=meshgrid(x0,y0); 3. Вычисление напряженности в узлах сетки: >> E1x=C*q.*(x-x1)./(sqrt(((x-x1).^2+y.^2).^3)); >> E1y=C*q.*y./(sqrt(((x-x1).^2+y.^2).^3)); >> E2x=C*q.*(x-x2)./(sqrt(((x-x2).^2+y.^2).^3)); >> E2y=C*q.*y./(sqrt(((x-x2).^2+y.^2).^3)); >> Ex=E1x+E2x; >> Ey=E1y+E2y; >> E=Ex.^2+Ey.^2; 4. Вычисление потенциала: >> R1=sqrt((x–x1).^2+y.^2); >> R2=sqrt((x–x2).^2+y.^2); >> P1=q./R1; >> P2=q./R2;  Рисунок 18. – Ввод исходных данных 5. Для построения графиков разобьем графическую область окна Figure на 4 подобласти с помощью функции subplot: >> subplot(2,2,1) Первое число указывает число окон по вертикали, второе – по горизонтали, третье – номер окна в которое будет выведен текущий график (нумерация окон слева – направо). 6. Строим график потенциала: >> surf(x, y, P); 7. Строим график величины напряженности в следующем окне: >> subplot(2,2,2); >> surf(x, y, E); 8. Для построения векторного поля напряженности воспользуемся функцией quiver: >> subplot(2,2,3); >> quiver(x, y, Ex, Ey); Данная функция строит векторное поле по значениям проекций вектора в данной точке. При этом необходимо следить, чтобы размерность x, y, Ex, Ey была одинаковой. 9. Построим графики сечений поверхности напряженности в направлении оси x и в направлении y следующим образом: >> subplot(2,2,4); >> plot(y0,E(:,10),'k.--',x0,E(10,:),'-o'); Полученный графический результат с использованием меню окна Figure. 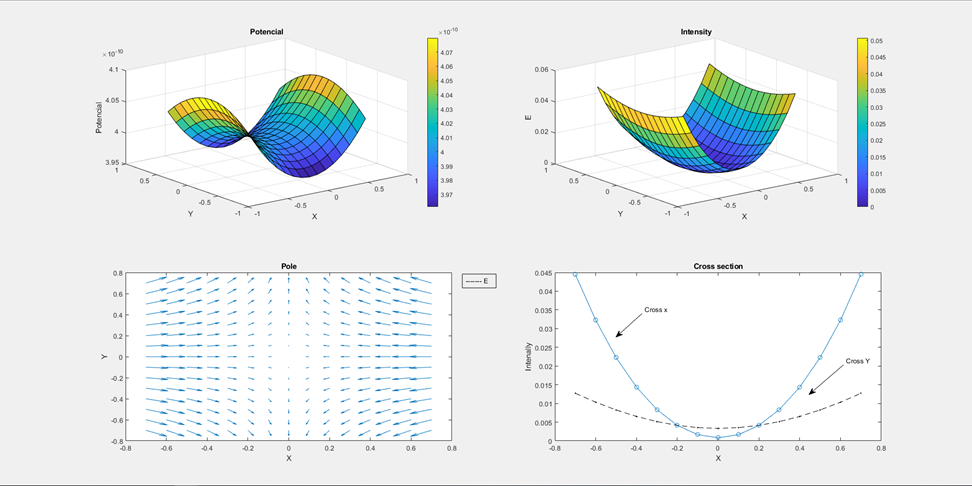 Рисунок 19. – Полученный результат с использованием окна Figure Вывод: получили навыки визуализации решения задач в системе MATLAB. В практической части лабораторной работы построили графическую интерпретацию решения задачи об определении электрического поля порождаемого двумя электрическими зарядами. |
