Расчетнографическая работа Программирование циклических алгоритмов с заданным числом повторений и управлений с условием. Расчет построение графиков функций и решение нелинейного уравнения

• Название: Расчетнографическая работа Программирование циклических алгоритмов с заданным числом повторений и управлений с условием. Расчет построение графиков функций и решение нелинейного уравнения
• Дата: 27.11.2018
• Размер: 302.51 Kb.
• Имя файла: Report_2_2_2.docx
• Тип: Решение; #57871

Омский государственный технический университет

Факультет информационных технологий и компьютерных систем

Кафедра «Информатика и вычислительная техника»

Расчетно-графическая работа

Программирование циклических алгоритмов с заданным числом повторений и управлений с условием. Расчет построение графиков функций и решение нелинейного уравнения

Выполнил:

студент гр. ИВТ-XxX

Преподаватель:

ст. преподаватель Дорошенко М.С.

Омск 2018г

Задание

Разработать схему алгоритма, написать и отладить программу для расчета и построения графиков двух функций (результаты расчетов должны храниться в виде массивов и распечатываться в виде таблицы), необходимо выделить наибольшее и наименьшее значение для каждой из функций.

Разработать программу нахождения корней уравнения f(x) = 0 на интервале [a, b] с точностью e = 0,001 (интервал подобрать или рассчитать самостоятельно):

2. x² - ln(x+1) + sin x -2 = 0.

Разработать программу для вычисления значения определенного интеграла на интервале [a,b] (a, b подобрать самостоятельно), численным методом прямоугольников и трапеций

2.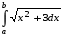

Математическая формулировка задания

1. 
   Для нахождения данных функции необходимо подставить текущее значение x в уравнения:
   

F1(x) = 1+2^x+5

F2(x) = (x-1)³

a = 1

b = 2

n = 18

2. 
   Алгоритм нахождения корня на интервале методом половинного деления (бисекций) сводиться к следующим действиям:
   

1. 
   Вычисляется середина интервала с = (а+b)/2;
   
2. 
   Если |f(c)| < e, где е – точность определения значения, то с будет являться приближенным значением корня уравнения и выводиться как результат расчетов;
   
3. 
   Если |f(c)| < e, то проверяются знаки ф-ий f(x) и f(c) на концах отрезка [a, c], для чего вычисляется их произведение. Если f(a)f(c)<0, то ф-ии будут иметь противоположные знаки и корень находится на отрезке [a,c]. В этом случае интервал [a, b] заменяется отрезком [a,c], для чего присвоим a=c;
   
4. 
   Вычисления по схеме п.1 – 4 повторяются в цикле до тех пор, пока не выполнится условие |f(c)| < e.
   

3. 
   Приближенное значение определенного интеграла вычисляется как сумма площадей n прямоугольников, построенных на интервале интегрирования [a, b]. Интервал [a, b] разбивается на N равных частей длинной h = (b-a)/ n, на каждой из которых строиться прямоугольник с высотой, равной значению ф-ии f(xi) в центре участка с координатой
   

xi=a+(i-0.5)h, где i = 1,2,…, N

Формула прямоугольников для приближенного вычисления значения интеграла будет иметь вид: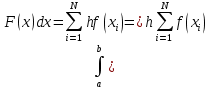



В методе трапеций интервал [a,b] разбивается на N равных частей длинной

h=(b-a)/N, на каждой из которых строится трапеция. Приближенное значение интеграла определяется суммой площадей трапеций, построенных на интервале [a,b], где xi=a+j*h.

Схемы алгоритмов

Данная расчетно-графическая работа состояла из нескольких задач: графическая заставка, построение графиков по рассчитанным таблицам, данные для которых были выведены из заданных формул, решение нелинейного уравнения методом трапеций и прямоугольников.

Первым пунктом работы является меню. Схема алгоритма представлена на рис.1

Графическая заставка была запрограммирована с помощью программного интерфейса OpenGL. Схема алгоритма представлена на рис. 2

Схема алгоритма для расчета таблиц приведена на рис.3, а схема алгоритмов построения графиков по этим таблицам на рис. 4

Схема алгоритма решения нелинейного уравнения методом бисекций представлена на рис. 5

Схема алгоритма вычисления интеграла разбита на две части: решение методом трапеций, методом прямоугольников(рис.6)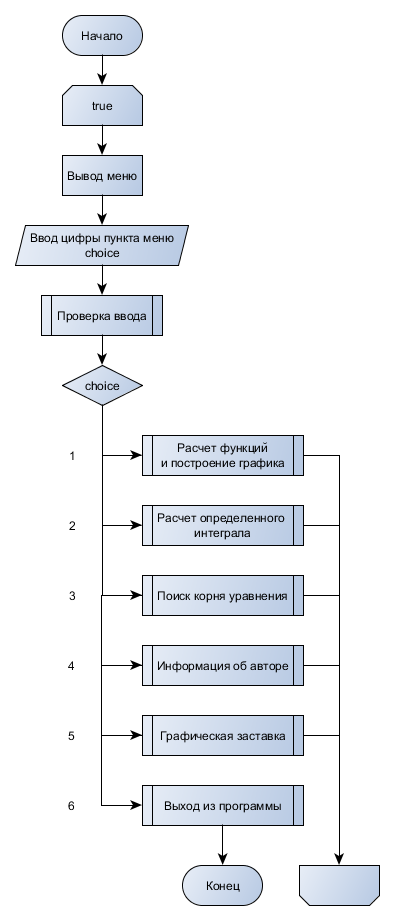



Рис.1 Схема алгоритма общая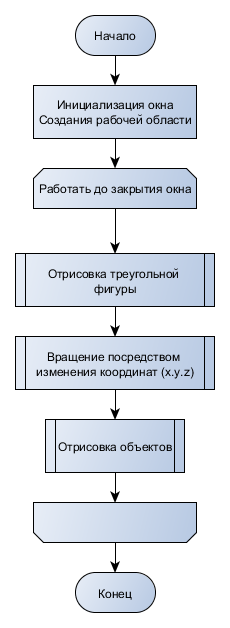



Рис.2 Алгоритм заставки

Табуляция функции

Для построения результатов двух функций использовано 2 одномерных массива.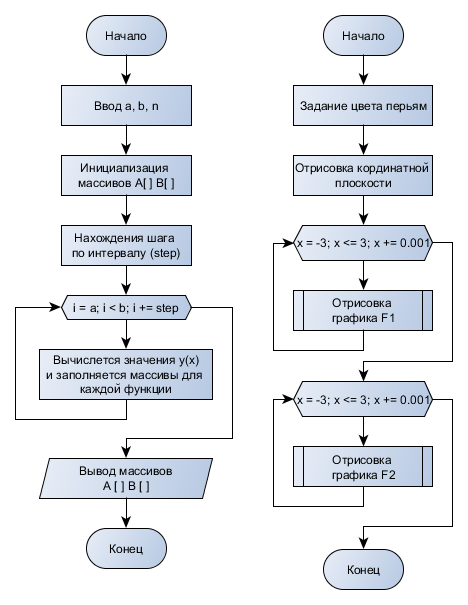



Рис. 3 – Алгоритм построения функций и построение графика



Рис.4 – Построение графика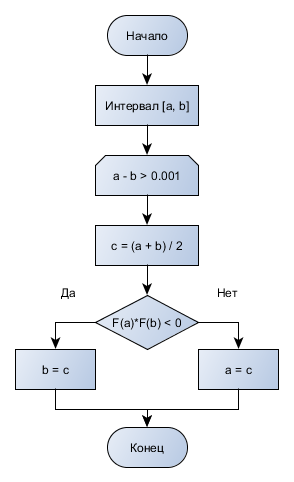



Рис. 5 – Решение нелинейного уравнения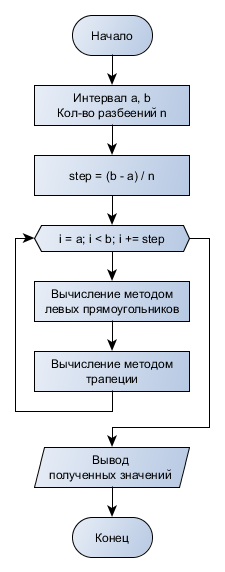



Рис.6 – Алгоритм решения определенного интеграла методом прямоугольников и трапеций

Код программы

#include

#include

#include

#include

#include

#include //библиотека для рисования заставки(установишь сам, ссылка ниже)

/*ИНСТРУКЦИЯ ДЛЯ УСТАНОВКИ GLUT: http://grafika.me/node/96*/
using namespace std;
float angle = 0.0f;

HANDLE handle = GetStdHandle(STD_OUTPUT_HANDLE);

// Вариант 3_18_20
void exerciseOne(int a, int b, int n); // Функция, выполняющая первое задание и выводящая результат

double func1(double x); // Функция, возвращающая значение F1 в точке X

double func2(double x); // Функция, возвращающая значение F2 в точке X

void exerciseTwo(double a, double b, double n); // Функция, выполняющая второе задание и выводящая результат

double funcInt(double x); // Функция, возвращающая значение подынтегральной функции в точке X

void exerciseThree(int a, int b); // Функция, выполняющая третье задание и выводящая результат

double funcEq(double x); // Функция, возвращающая значение функции уравнения в точке X

void about(); // Функция, возвращающая информацию об авторе

void bildGraph(); // Функция, рисующая заставку

bool check(char val, char sizeMenu);
bool exitProgramm;
/*********ЗАСТАВКА***************/

void changeSize(int w, int h) {

// предотвращение деления на ноль

if (h == 0)

h = 1;

float ratio = w * 1.0 / h;

// используем матрицу проекции

glMatrixMode(GL_PROJECTION);

// обнуляем матрицу

glLoadIdentity();

// установить параметры вьюпорта

glViewport(0, 0, w, h);

// установить корректную перспективу

gluPerspective(45.0f, ratio, 0.1f, 100.0f);

// вернуться к матрице проекции

glMatrixMode(GL_MODELVIEW);

}
void renderScene(void) {

// очистка буфера цвета и глубины

glClear(GL_COLOR_BUFFER_BIT | GL_DEPTH_BUFFER_BIT);

// обнуление трансформации

glLoadIdentity();

// установка камеры

gluLookAt(0.0f, 0.0f, 10.0f,

0.0f, 0.0f, 0.0f,

0.0f, 1.0f, 0.0f);
glRotatef(angle, 0.0f, 1.0f, 0.0f);
glBegin(GL_TRIANGLES);

glVertex3f(-2.0f, -2.0f, 0.0f);

glVertex3f(0.0f, 2.0f, 0.0);

glVertex3f(2.0f, -2.0f, 0.0);

glEnd();
angle += 0.1f;
glutSwapBuffers();

}

//функция вызова заставки

void Screensaver(int argc, char **argv)

{

glutInit(&argc, argv);

glutInitDisplayMode(GLUT_DEPTH | GLUT_DOUBLE | GLUT_RGBA);

glutInitWindowPosition(100, 100);

glutInitWindowSize(400, 400);

glutCreateWindow("Урок 3");
// регистрация

glutDisplayFunc(renderScene);

glutReshapeFunc(changeSize);

glutIdleFunc(renderScene);
// основной цикл

glutMainLoop();

}

/************************************/
int main(int argc, char **argv)

{

setlocale(LC_ALL, "RUS");

exitProgramm = false;

char choice;

while (true) {

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\n\n\n\n\n\n\n\n");

printf("\t\t\t\t\t========== Расчетно-графичекая работа ==========\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

printf("\t\t\t\t\t==== 1. Расчет функций и построение графика ====\n");

printf("\t\t\t\t\t==== 2. Расчет определенного интеграла ====\n");

printf("\t\t\t\t\t==== 3. Поиск корня уравнения ====\n");

printf("\t\t\t\t\t==== 4. Информация об авторе ====\n");

printf("\t\t\t\t\t==== 5. ГРАФИЧЕСКАЯ ЗАСТАВКА ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t==== 6. Выход из программы ====\n");

printf("\t\t\t\t\t================================================\n");

SetConsoleTextAttribute(handle, FOREGROUND_GREEN);

printf("\t\t\t\t\t>>>> Ввод: ");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

cin >> choice;

if (!check(choice, '6')) {

system("cls");

printf("Введено неверное значение. Попробуй еще раз\n");

continue;

}

switch (choice) {

case '1': { exerciseOne(1, 2, 18); break; }

case '2': { exerciseTwo(2.0, 20.0, 100.0); break; }

case '3': { exerciseThree(0, 1); break; }

case '4': { about(); break; }

case '5': { Screensaver(argc, argv); break; }

case '6': { exitProgramm = true; break; }

}
if (exitProgramm) {

break;

}

}
cout << "\n\n";

system("PAUSE");

return 0;

}
void exerciseOne(int a, int b, int n) {

system("CLS");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\n\n\n\n\n\n\n\n");

printf("\t\t\t\t\t===== Расчет функций и построение графика =====\n");

printf("\t\t\t\t\t================================================\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

double step = (b - a)*pow(n, -1);

double* f1Val = new double[n];

double* f2Val = new double[n];
int iter = 0;

for (double i = a; i < b; i += step) {

f1Val[iter] = func1(i);

f2Val[iter] = func2(i);

iter++;

}
for (int i = 0; i < n; i++) {

cout << "\t\t\t\t\t==== " << i << " | " << f1Val[i] << " |\t " << f2Val[i] << "\n";

}
char choice;

int infintyCycle = true;

while (infintyCycle) {

SetConsoleTextAttribute(handle, FOREGROUND_GREEN);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t==== 1. Построить графики ====\n");

printf("\t\t\t\t\t==== 2. Выйти в главное меню ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t==== 3. Выйти из программы ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t>>>> Ввод: ");

cin >> choice;

if (!check(choice, '3')) {

system("cls");

printf("\t\t\t\t\tВведено неверное значение. Попробуй еще раз\n");

continue;

}

switch (choice) {

case '1': { bildGraph(); }

case '2': { infintyCycle = false; break; }

case '3': { infintyCycle = false; exitProgramm = true; break; }

}

system("cls");

}

}
double func1(double x) {

return pow(2, (x + 5) + 1);

}
double func2(double x) {

return pow((x - 1), 3);

}
void exerciseTwo(double a, double b, double n) {

system("CLS");

printf("\n\n\n\n\n\n\n\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t===== Расчет определенного интеграла =====\n");

printf("\t\t\t\t\t================================================\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

double step = (b - a)*pow(n, -1);

double square = 0;

double trapeze = 0;
for (double i = a; i < b; i += step) {

square += step * funcInt(i);

trapeze += (funcInt(i) + funcInt(i - step)) * step * pow(2, -1);

}
cout << "\t\t\t\t\t==== Метод левых прямоугольников: " << square << "\n\t\t\t\t\t==== Метод трапеции: " << trapeze << "\n";

char choice;

bool infintyCycle = true;

while (infintyCycle) {

SetConsoleTextAttribute(handle, FOREGROUND_GREEN);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t==== 1. Выйти в главное меню ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t==== 2. Выйти из программы ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t>>>> Ввод: ");

cin >> choice;

if (!check(choice, '2')) {

system("cls");

printf("\t\t\t\t\tВведено неверное значение. Попробуй еще раз\n");

continue;

}

switch (choice) {

case '1': { infintyCycle = false; break; }

case '2': { infintyCycle = false; exitProgramm = true; break; }

}

system("cls");

}

}
double funcInt(double x) {

return pow(x*x + 3, 1/2);

}
void exerciseThree(int left, int right) {

system("CLS");

printf("\n\n\n\n\n\n\n\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t===== Поиск корня уравнения =====\n");

printf("\t\t\t\t\t================================================\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

double a = left, b = right, c;

while (abs(a - b) > 0.001) {

c = (a + b) * pow(2, -1);

if (funcEq(a)*funcEq(c) < 0) {

b = c;

}

else {

a = c;

}

}
cout << "\t\t\t\t\t==== Решение: " << c << "\n";
char choice;

bool infintyCycle = true;

while (infintyCycle) {

SetConsoleTextAttribute(handle, FOREGROUND_GREEN);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t==== 1. Выйти в главное меню ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t==== 2. Выйти из программы ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t>>>> Ввод: ");

cin >> choice;

if (!check(choice, '2')) {

system("cls");

printf("\t\t\t\t\tВведено неверное значение. Попробуй еще раз\n");

continue;

}

switch (choice) {

case '1': { infintyCycle = false; break; }

case '2': { infintyCycle = false; exitProgramm = true; break; }

}

system("cls");

}

}
double funcEq(double x) {

return pow(x, 2) - log(x - 1) + sin(x) - 2;

}
void about() {

system("CLS");

printf("\n\n\n\n\n\n\n\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t========== Информация об авторе ==========\n");

printf("\t\t\t\t\t================================================\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

printf("\t\t\t\t\t===== ФИО ОмГТУ 2018 =====\n");

printf("\t\t\t\t\t===== ПРОЧАЯ ИНФОРМАЦИЯ =====\n");

printf("\t\t\t\t\t================================================\n");

char choice;

bool infintyCycle = true;

while (infintyCycle) {

SetConsoleTextAttribute(handle, FOREGROUND_GREEN);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t==== 1. Выйти в главное меню ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_RED);

printf("\t\t\t\t\t==== 2. Выйти из программы ====\n");

SetConsoleTextAttribute(handle, FOREGROUND_INTENSITY);

printf("\t\t\t\t\t================================================\n");

printf("\t\t\t\t\t>>>> Ввод: ");

cin >> choice;

if (!check(choice, '2')) {

system("cls");

printf("\t\t\t\t\tВведено неверное значение. Попробуй еще раз\n");

continue;

}

switch (choice) {

case '1': { infintyCycle = false; break; }

case '2': { infintyCycle = false; exitProgramm = true; break; }

}

system("cls");

}

}
void bildGraph() {

int kx = 35;

int ky = 3;

int offset_x = 500;

int offset_y = 230;

system("cls");

double x;

HDC hDC = GetDC(GetConsoleWindow());

HPEN Pen2 = CreatePen(PS_SOLID, 2, RGB(0, 255, 255));

HPEN Pen = CreatePen(PS_SOLID, 2, RGB(255, 255, 255));

HPEN Pen1 = CreatePen(PS_SOLID, 2, RGB(255, 0, 0));

SelectObject(hDC, Pen);
//x

TextOutA(hDC, 820, 200, "X", 1);

MoveToEx(hDC, 100, 230, NULL);

LineTo(hDC, 850, 230);
//y

TextOutA(hDC, 480, 10, "Y", 1);

MoveToEx(hDC, 500, 10, NULL);

LineTo(hDC, 500, 800);
//центр(0): y = 500 x = 230

TextOutA(hDC, 490, 200, "0", 1);
SelectObject(hDC, Pen1);
MoveToEx(hDC, kx*-10, -ky * func1(-10) + offset_y, NULL);
//TextOutA(hDC, 320, 80, "|x+10|^5", 28);

for (x = -10; x <= 10; x += 0.001)

{

LineTo(hDC, kx*x + offset_x, -ky * func1(x) + offset_y);

}
SelectObject(hDC, Pen2);

//TextOutA(hDC, 320, 225, "1+2^(x+5)", 10);
MoveToEx(hDC, kx*-10, -ky * func2(-10) + offset_y, NULL);
for (x = -10; x <= 10; x += 0.001)

{

LineTo(hDC, kx*x + offset_x, -ky * func2(x) + offset_y);

}

system("pause");

}
bool check(char val, char sizeMenu) {

if (val > '0' && val <= sizeMenu)

return true;

else

return false;

}

Результаты программы

Консольное приложение, точнее его меню, представлено на рисунке 7. Ниже будут представлены пункты меню.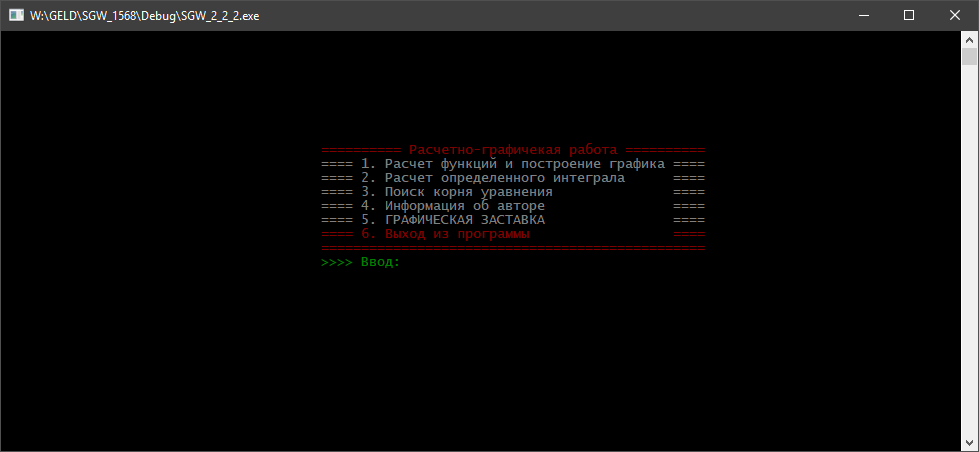



Рис.7 - Общий вид меню



Рис. 8 – Сведения об авторе



Рис. 9 – Таблица значений двух функций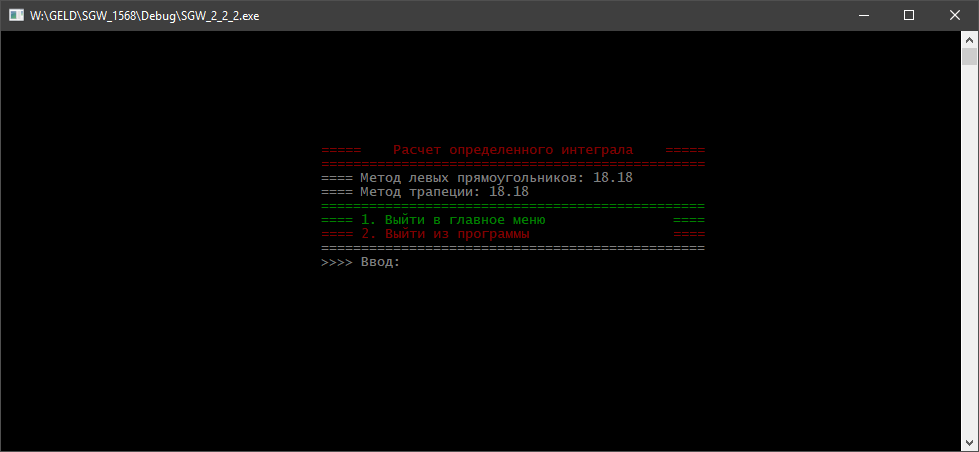



Рис.11 – Решение определенного интеграла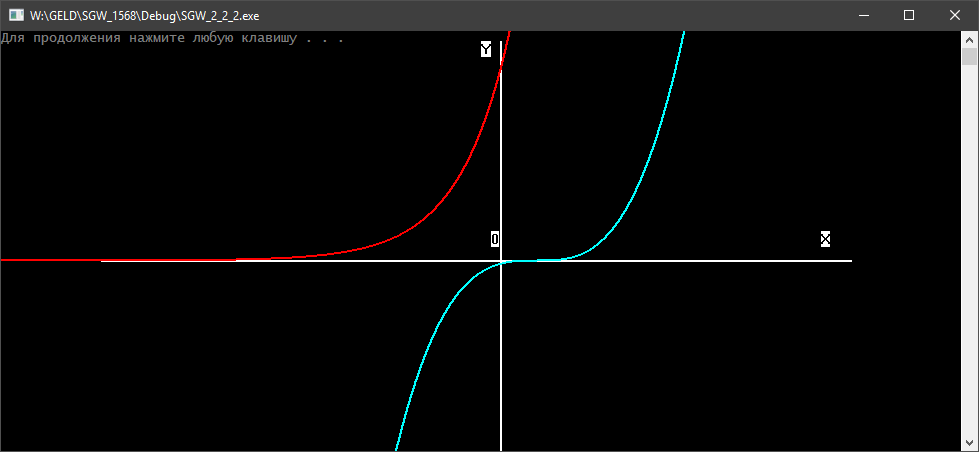



Рис.12 – График ф-ии по таблице

Решение нелинейного уравнения

Найдем минимум функции:

x2 - ln(x+1) + sin x -2 = 0.

Используем для этого метод половинного деления (метод дихотомии)..

Решение:

Возьмем отрезок разбиения [a,b], такой, что f(a)<0e будем выполнять циклично следующие операции:

1. 
   найдем среднюю точку отрезка [a,b] c = (a+b)/2;
   
2. 
   если f(c)=0, то корень найден, КОНЕЦ;
   
3. 
   если f(a)*f(c)<0, тогда b=c, иначе a=c.
   

Так далее пока длинна отрезка не станет |b_n-c_n| >e

Решение интеграла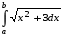



Метод прямоугольника

Вычислим шаг разбиения (длину каждого промежуточного отрезка):

h = b-a/n;

f(b до a) = ?
Теперь сложим полученные результаты и умножим на шаг h, тем самым получим интеграл на отрезке [a,b]:

I = (h*))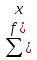

Метод прямоугольника

Вычислим шаг разбиения (длину каждого промежуточного отрезка):

h = b-a/n; x₀=a

Найдем кол-во точек x

X_i = X₀ + X_n + h;

X₀ = 2; X₁ = 2 + 0,6 = 2,6; X₂ = 2,6 + 0,6 = 3,2; X₃ = 3,2 + 0,6 =3,8; X₄ = 3,8 + 0,6 = 4,4; X₅ = 4,4 + 0,6 = 5;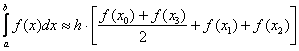



По формуле трапеций вычислим интеграл, сначала найдем значения f(x):

f(2 до 5 с шагом 0,6) = ?;

Подставляем полученные значения в формулу трапеций.

Список используемой литературы

1. 
   О.П. Шафеева Методы проектирования программ.-Ом.:Издательство ОмГТУ, 2004
   
2. 
   О.П. Шафеева Практикум по программированию на языке С.-Ом.:Издательство ОмГТУ, 2008
   
3. 
   http://mathprofi.ru/formula_simpsona_metod_trapecij.html
   

4. http://mathprofi.ru/metod_prjamougolnikov.html