01УправлИинформ2020. Информатика информатика это комплекс дисциплин по решению проблем управления системами с применением их моделей на компьютере. Тема информация и управление

• Название: Информатика информатика это комплекс дисциплин по решению проблем управления системами с применением их моделей на компьютере. Тема информация и управление
• Дата: 30.05.2022
• Размер: 0.73 Mb.
• Имя файла: 01УправлИинформ2020.docx
• Тип: Документы; #558527
• страница: 6 из 6

2. Двоичная система счисления

В вычислительной технике, в устройствах автоматики и связи широко используется двоичная система счисления. Это связано с тем, что в таких устройствах используются элементы с двумя устойчивыми состояниями (например, есть заряд на конденсаторе или нет). Двоичная система – это система с наименьшим возможным основанием. В ней для изображения числа используются только две цифры: 0 и 1.

Произвольное число в двоичной системе счисления представляется в виде полинома:

X = а_m*2^m+а_m-1*2^m-1+...+а₁*2¹ +а₀*2⁰+а_-1*2^-1 +...+а _{- m}*2^-m . (3)

Примеры чисел в двоичной системе счисления:

1 = 1₂ 2 = 10₂ 3 = 11₂ 4 = 100₂ 5 = 101₂ 0.5 = 0.1₂ 0.25 = 0.01₂

Таблица сложений чисел в двоичной системе счисления имеет вид

0+0=0 0+1=1 1+0=1 1+1=10

Таблица умножений чисел в двоичной системе счисления имеет вид

0*0=0 0*1=0 1*0=0 1*1=1

3. Восьмеричная и шестнадцатеричная системы счисления

В вычислительной технике используются и другие позиционные системы: восьмеричная и шестнадцатеричная.

СИСТЕМЫ СЧИСЛЕНИЯ R=2,8,16

Базисные числа

Двоич. Дес. 8 Шест. Двоич. Дес. 8 Шест.
0000 0 0 0 1000 8 10 8

0001 1 1 1 1001 9 11 9

0010 2 2 2 1010 10 12 A

0011 3 3 3 1011 11 13 B

0100 4 4 4 1100 12 14 C

0101 5 5 5 1101 13 15 D

0110 6 6 6 1110 14 16 E

0111 7 7 7 1111 15 17 F

Ввосьмеричной системе счисления базисными числами являются 0, 1, 2, 3, 4, 5, 6, 7. Запись любого числа в этой системе основывается на его разложении по степеням числа восемь с коэффициентами из базисного набора.

Вшестнадцатеричной системе счисления базисными являются числа от нуля до пятнадцати. Для обозначения первых девяти чисел используются арабские числа от нуля до девяти, остальные обозначаются латинскими буквами a, b, c, d, e, f.

4. Перевод чисел из одной системы счисления в другую

При решении задач с помощью ЭВМ исходные данные обычно задаются в десятичной системе счисления; в этой же системе, как правило, нужно получать и окончательные результаты. Поскольку в современных ЭВМ данные кодируются в основном в двоичных кодах, то возникает задача перевода чисел из одной системы счисления в другую.

Ограничимся рассмотрением систем счисления, у которых базисными числами являются последовательные числа 0, 1,... R-1, где R – основание системы. Задача перевода заключается в следующем.

Пусть известна запись числа х в системе счисления с основанием R:

R_n R_n-1... R₁ R₀ R_-1 R_-2...,

где R_i – цифры R-ичной системы. Требуется найти запись этого же числа в системе с основанием Q:

Q_n Q_n-1... Q₁ Q₀ Q_-1 Q_-2...,

где R_i – цифры R-ичной системы, Q_i – цифры Q-ичной системы

Способ 1. Перевод чисел из Q в Р-ичную систему

Перевод Q → P. Задача сводится к вычислению полинома вида

Х = a_nQⁿ + a_n-1Q^n-1 +...+a₁Q¹ + a₀Q⁰ + a_-1Q^-1 +...+ a _-mQ^-m. (4)

Для получения P-ичного изображения (4) необходимо все цифры ai и число Q заменить P-ичными изображениями и выполнить арифметические операции в P-ичной системе счисления.

Пример. Перевести х = 371₈ в десятичную систему счисления.

Запишем число 371₈ в виде х = 3*8² +7*8¹ + 1*8⁰ и выполним все необходимые действия в десятичной системе:

х = 3*64 + 7*8 + 1 = 192+56+1 = 249.

Способ 2. Перевод чисел из Р в Q-ичную систему

Перевод P → Q. Рассмотрим случай перевода целых чисел. Пусть известна запись целого числа N в системе счисления с основанием P и требуется перевести это число в систему с основанием Q. Поскольку N – целое, то его запись в Q-ичной системе счисления имеет вид

N = a_s a_s-1 ... a₁ a₀,

где a_i – искомые цифры Q-ичной системы. Для определения a0 разделим обе части равенства

N = a_sQ^s + a_s-1Q^s-1 +...+a₁Q¹ + a₀ (5)

на число Q, причем в левой части произведем деление, пользуясь правилами P-ичной арифметики, а правую часть перепишем в виде

N/Q = a_sQ^s-1 + a_s-1Q^s-2 +...+a₁ + a₀/Q.

Приравниваем между собой полученные целые и дробные части (учитывая, что a_i < Q):

[N/Q] = a_sQ^s-1 + a_s-1Q^s-2 +...+a₁,

[N/Q] = a₀/Q.

Таким образом, младший коэффициент a₀ в разложении (5) определяется соотношением

a₀ = Q[N/Q].

Положим

N₁ = [N/Q] = a_sQ^s-1 + a_s-1Q^s-2 +...+a₁.

Тогда N₁ будет целым числом и к нему можно применить ту же самую процедуру для определения следующего коэффициента a₁ и т. д.

Таким образом, при условии, что N₀ = N, перевод чисел с использованием

Р-ичной арифметики осуществляется по следующим рекуррентным формулам

a_i = Q[N_i/Q], (6)

N_{i +1} = [N_i /Q], (i = 0, 1, 2, ...)

Этот процесс продолжается до тех пор, пока не будет получено N_{i +1} = 0. Пример. Перевести число N = 47 в двоичную систему. Применяя формулы (6) при Q=2, имеем

47:2 = 23(1); 23:2 = 11(1); 11:2 = 5(1); 5:2 = 2(1); 2:2 = 1(0); 1:2 = 0(1).

Поскольку числа нуль и единица в обеих системах счисления обозначаются одинаковыми цифрами 0 и 1, то в процессе деления сразу получим двоичные изображения искомых цифр:

N = 101111₂.

Примеры перевода чисел из одной системы счисления в другую

Наиболее часто встречающиеся системы счисления – это двоичная, шестнадцатеричная и десятичная. Как же связаны между собой представления числа в различных системах счисления? Рассмотрим различные способы перевода чисел из одной системы счисления в другую на конкретных примерах.

Способ 1. Пусть требуется перевести число 567 из десятичной в двоичную систему. Сначала определим максимальную степень двойки, такую, чтобы два в этой степени было меньше или равно исходному числу. В нашем случае это 9, так как 2⁹=512, а 2¹⁰=1024, что больше начального числа. Таким образом, мы получим число разрядов результата. Оно равно 9+1=10. Поэтому результат будет иметь вид 1ххххххххх, где вместо х могут стоять любые двоичные цифры. Найдем вторую цифру результата. Возведем двойку в степень 9 и вычтем из исходного числа: 567-2⁹=55. Остаток сравним с числом 2⁸=256. Поскольку 55 меньше 256, то девятый разряд будет нулем, т. е. результат примет вид 10хххххххх. Рассмотрим восьмой разряд. Поскольку 2⁷=128>55, то и он будет нулевым.

Седьмой разряд также оказывается нулевым. Искомая двоичная запись числа принимает вид 1000хххххх. 2⁵=32<55, поэтому шестой разряд равен 1 (результат 10001ххххх). Для остатка 55-32=23 справедливо неравенство 2⁴=16<23, что означает равенство единице пятого разряда. Действуя аналогично, получаем в результате число 1000110111. Мы разложили данное число по степеням двойки:

567=1*2⁹+0*2⁸+0*2⁷+0*2⁶+1 *2⁵+1*2⁴+0*2³+1 *2² +1 *2¹+1 *2⁰ .

Способ 2. При другом способе перевода чисел используется операция деления в столбик.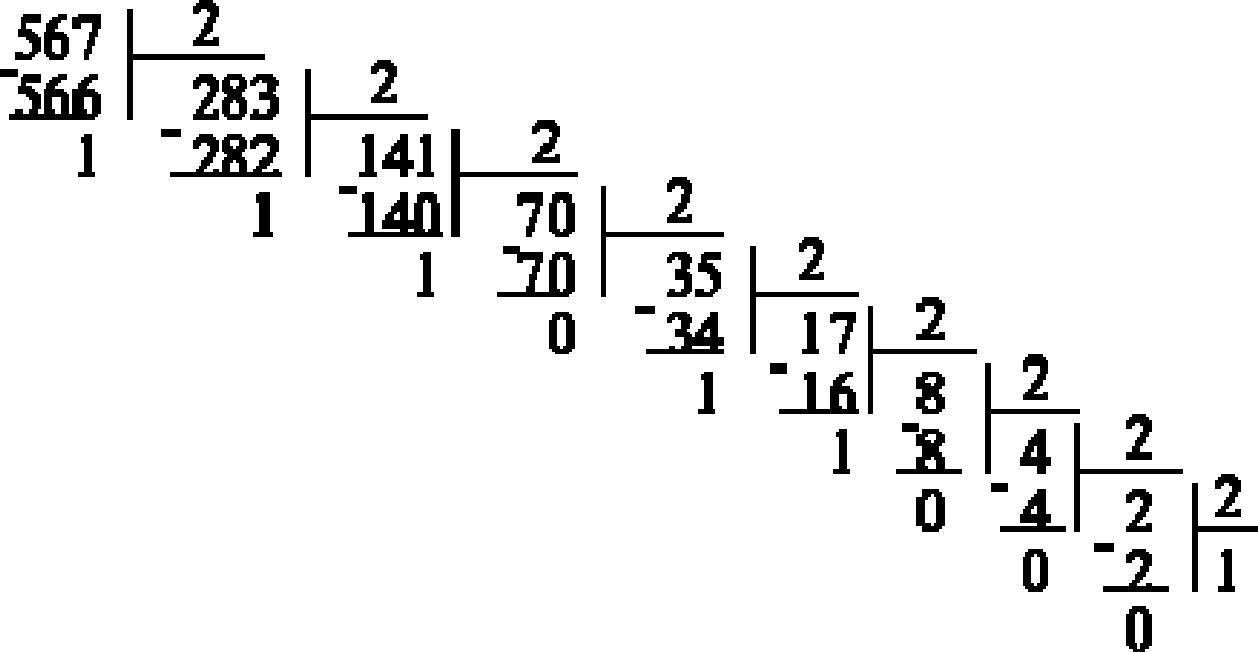



Рассмотрим число 567. Разделив его на 2, получим частное 283 и остаток 1.

Проведем ту же самую операцию с числом 283. Получим частное 141, остаток 1. Опять делим полученное частное на 2, и так до тех пор, пока частное не станет меньше делителя. Теперь для того, чтобы получить число в двоичной системе счисления, достаточно записать последнее частное, то есть 1 и приписать к нему справа в обратном порядке все полученные в процессе деления остатки. Результат, естественно, не изменился: 567 в двоичной системе счисления записывается как 1000110111.

Эти два способа применимы при переводе числа из десятичной системы в систему с любым основанием. Для закрепления навыков рассмотрим перевод числа 567 в систему счисления с основанием ₁₆.

Способ последовательного деления в столбик, с единственным отличием в том, что делить надо не на 2, а на 16. Процесс деления заканчивается, когда частное становится меньше 16.

Конечно, не надо забывать и о том, что для записи числа в шестнадцатерич­ной системе счисления необходимо заменить 10 на A, 11 на B и так далее.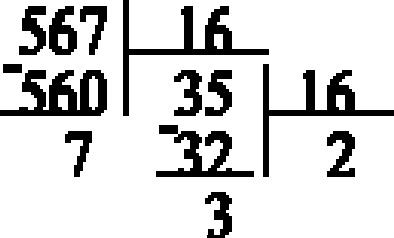


Для того, чтобы получить число в шестнадцатеричной системе счисления, достаточно записать последнее частное, то есть 2, приписать к нему справа в обратном порядке все полученные в процессе деления остатки. Результат, естественно, не изменился: 567 в шестнадцатеричной системе счисления записывается как 237₁₆.

Операция перевода в десятичную систему выглядит гораздо проще, так как любое число можно представить в виде

x = a₀*Rⁿ + a₁*R^n-1 + ... + a_n-1^*R¹ + a_n*R⁰,

где a₀ ... a_n – это цифры данного числа в системе счисления с основанием R. Подставим вместо цифр базисные числа и десятичное представление R. Например, переведем число 4A3F в десятичную систему. По определению,

4A3F = 4*16³ + A*16² + 3*16 + F.

Заменив A на 10, а F на 15, получим

4*16³ + 10*16² + 3*16 + 15 = 19007.

5. Перевод чисел в системах с основаниями 2, 8, 16

Пожалуй, проще всего осуществляется перевод чисел из двоичной системы в системы с основанием, равным степеням двойки (8 и 16), и наоборот. Для того чтобы целое двоичное число записать в системе счисления с основанием 2ⁿ, (n = 4 для шестнадцатеричных чисел и n = 3 для восьмерич­ных чисел) нужно:

• 
  заданное двоичное число разбить справа налево на группы по n цифр в каждой;
  
• 
  если в последней левой группе окажется меньше n разрядов, то дополнить ее нулями до нужного числа разрядов;
  
• 
  рассмотреть каждую группу как n-разрядное двоичное число и заменить ее соответствующей цифрой в системе счисления с основанием 2n (таблицы 1 и 2).
  

Таблица 1. Двоично-шестнадцатеричная таблица

2-ная__0000__0001__0010__0011'>2-ная	0000	0001	0010	0011	0100	0101	0110	0111
16-ная	0	1	2	3	4	5	6	7
2-ная	1000	1001	1010	1011	1100	1101	1110	1111
16-ная	8	9	A	B	C	D	E	F

Таблица 2. Двоично-восьмеричная таблица

2-ная	000	001	010	011	100	101	110	111
8-ная	0	1	2	3	4	5	6	7

Вопросы для самопроверки

Переведите в десятичную систему счисления: а) 10001110₂; б) 12345₈; в) AA02D34B₁₆.

Сравните два числа:

а) 1026₈ и 2161₆; в) 11111₂ и 11111₃.