Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
Сжатие векторных данных Рассматривая растровые модели данных, мы обнаружили, что данные могут быть упакованы разными способами для сокращения объема занимаемой памяти. Хотя векторные модели более эффективны при хранении больших объемов пространственных данных, нам все же нужно рассмотреть компрессию. Метод сжатия, который мы сейчас рассмотрим, на самом деле довольно похож на простой процесс кодирование, разработанный более века назад сэром Фрэнсисом Гальтоном [Francis Galton, 1884]. Будет полезно переместиться во времени и присоединиться к английскому ученому, когда он пытался создать рукописную схему записи направлений во время географических экскурсий. Форма, придуманная им, - сама простота. Он просто использовал восемь чисел для обозначения четырех главных и четырех промежуточных географических направлений (Рисунок 4.16а). Удивительно похожая модель кодирования, разработанная в наше время, известна как цепочечные коды Фримэна-Хофмэна [Freeman, 1974] (Рисунок 4.16b). Целые числа от 0 до 7 назначаются восьми векторам направлений. Метод Фримэна-Хофмэна использует те же главные и промежуточные направления для векторов, что и Гальтон в своих путешествиях для наземной навигации. Назначая длину для каждого вектора, мы можем записывать отдельные линейные объекты, указывая их начало, длину, направление, в котором они рисуются и где они меняют направление. Существуют многие вариации на эту тему, включая увеличение количества кодов до 16-ти (Рисунок 4.16с) или даже до 32-х для увеличения точности. Результат один - сокращение объема векторной БД. 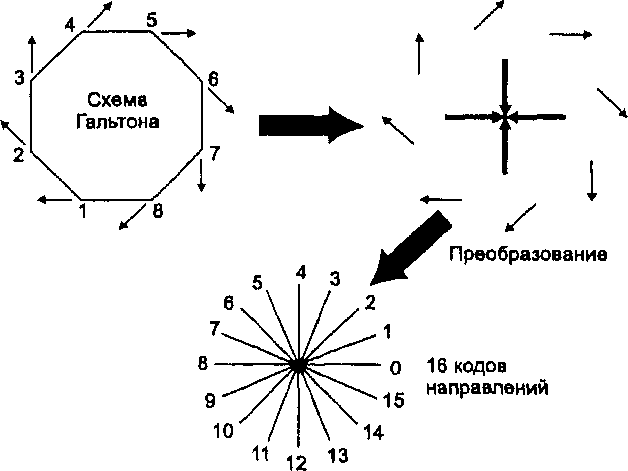 Рисунок 4.16. Цепочечные коды. Сравнение компактных моделей для указания направлений: разработанной сэром Фрэнсисом Гальтоном и усовершенствованной в виде цепочечных кодов Фримэна-Хофмэна. Обратите внимание на сильное сходство между старой и новой моделями. Хотя модели цепочечных кодов существенно экономят память, они, как и спагетти-модель, не содержат явной топологической информации. Это ограничивает их полезность для функций хранения, выборки и вывода из-за аналитических ограничений нетопологических структур данных. Кроме того, тот способ, которым кодируются линии и области в виде векторов, при выполнении преобразований координат, особенно поворотов, вызывает значительные накладные вычислительные расходы. Модели цепочечных кодов хороши для определения расстояний и форм, поскольку большая часть этой информации имеется в самих направляющих векторах. И поскольку этот подход очень похож нато, как работают векторные плоттеры (см. Главу 14), эти модели эффективны для выполнения быстрого вывода на плоттер. Векторная модель для представления поверхностей До сих пор мы игнорировали поверхности, хотя они являются фундаментальными явлениями, которые мы моделируем с помощью ГИС. Они существенно различаются по способам представления, особенно векторным. В растре географическое пространство подразумевается дискретным, каждая ячейка растра занимает определенную площадь. В пределах этого дискретизированного, или квантованного, пространства ячейка может иметь атрибут абсолютного значения высоты, которое наиболее представительно для этой ячейки. Это может быть наивысшее или наинизшее значение или некая средняя величина высоты. Таким образом, существующие растровые структуры данных вполне способны представлять поверхности. 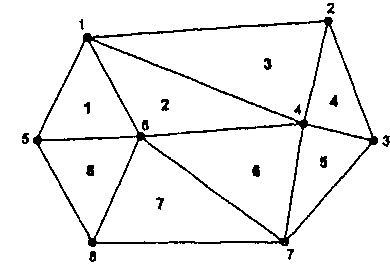
 Рисунок 4.17. Модель TIN. Векторное представление поверхностей образуется соединением точек с известными значениями высоты. Модель называется нерегулярной триангуляционной сетью (TIN). Но в случае векторов картина совсем другая. Как вы помните, большая часть пространства между графическими примитивами подразумевается, а не определяется явным образом. Для определения этого пространства именно как поверхности мы должна квантовать ее неким способом, который сохраняет важные изменения поверхностной информации и косвенно выражает области с одинаковыми данными высоты. Простой способ представить себе это - рассмотреть как минералоги или кристаллографы описывают минералы. Каждый кристалл имеет набор гладких граней, соединенных точками и линиями, которые показывают значительные смены в его структуре. Аналогично, мы можем представить себе топографическую поверхность в виде природного кристалла с его плоскими гранями, ребрами и вершинами (Рисунок 4.17). Таким образом, мы можем моделировать поверхность, создавая последовательности регулярно или нерегулярно распределенных точек. Каждая точка имеет явно заданную высоту. Проводя через три близлежащие точки плоскость, мы можем изобразить треугольную область постоянного уклона. Полученные таким образом треугольники создают структуру, представляющую по сути "кристаллоподобную" модель нашей поверхности. Эта модель, называемая нерегулярной триангуляционной сетью (triangulated irregular network (TIN)), позволяет нам использовать для описания рельефа точки некоторой сетки. Точки могут размещаться как регулярно, так и нерегулярно. Для получения модели поверхности нам нужно соединить пары точек ребрами определенным способом, называемым триангуляцией. Тогда, при необходимости получения трехмерного представления, TIN может быть показана в виде проволочной модели или модели с закрашенными гранями. Кроме построения TIN, точечные данные могут использоваться для традиционного представления поверхностей изолиниями. Это особенно элегантное средство представления поверхностей на самом деле использовалось в качестве главной структуры данных в ранних системах работы с данными поверхностей [DeMers and Fisher, 1991]. Мы вернемся к модели TIN в Главе 10. Гибридные и интегрированные системы Мы прошли путь усложнения от файловых структур через СУБД к моделям пространственных данных. Теперь нам нужно сделать еще один шаг на пути к законченным системам. Большинство растровых систем просты настолько, что сама модель данных дает относительно полное описание. В векторных же системах существуют два основных подхода к интеграции графических элементов модели данных с БД атрибутов. Полезно рассмотреть эти две модели не только потому, что они различаются в основе, но и потому, что векторные ГИС сейчас доминируют на рынке. Двумя главными типами векторных ГИС являются интегрированные и гибридные системы.* Файлы координат и топологии База данных  Рисунок 4.18. Гибридная векторная ГИС с хранением атрибутов во внешней БД. Файлы графических данных программно связываются с СУБД, хранящей атрибутивную информацию. * Следует различать два смысла термина "гибридные" применительно к ГИС. Им могут обозначаться системы, интегрирующие растровые и векторные данные, а также системы, хранящие графические и атрибутивные данные в различных файлах или графику - в файлах, а атрибуты - под управлением внешней СУБД. Системы с раздельных хранением графики и атрибутов называются также геореляционными. Существование гибридной модели данных ГИС - подтверждение того, что хотя ее структуры данных эффективны по отношению к графическим характеристикам объектов, им не достает той же эффективности в управлении атрибутивными данными [Aronson, 1985; Morehouse, 1985]. И наоборот, СУБД общепризнанны как средство управления атрибутивными типами данных, но плохо приспособлены к работе с графическими объектами. Выглядит вполне логичным, что программное объединение этих двух технологий позволит взять лучшее из каждой. Для реализации этого подхода координатные и топологические данные, требуемые для графики, хранятся как отдельный набор файлов (Рисунок 4.18). Таблицы атрибутов, содержащие все необходимые описательные данные для каждого графического объекта, хранятся отдельно либо в других файлах, либо под управлением СУБД общего назначения. Связь между графикой и атрибутами осуществляется через идентификационные коды графических объектов, имеющиеся в графических файлах, и которые также хранятся в отдельной колонке атрибутивной БД. Благодаря возможности внешнего хранения многих атрибутов для каждого объекта растут аналитические возможности и возможна экономия памяти. В число гибридных входят основанные на САПР системы INTERGRAPH IGDS/DMRS, векторно-топологические ARC/INFO, GEOVISION, и INTERGRAPH MGE, а также по меньшей мере одна основанная на квадродереве система SPANS. Подробное рассмотрение этих систем выходит за рамки данной книги, и мы отсылаем читателя к справочным работам по ГИС и СУБД [Healey, 1991; Maquire, Goodchild, and Rhind, 1991]. Другим подходом к хранению графических и атрибутивных данных является интегрированная модель данных. В этом случае ГИС является процессором пространственных запросов, надстроенным над стандартной СУБД, которая используется для хранения как атрибутивной, так и графической информации [Guptill, 1987; Morehouse, 1989]. Интегрированная система хранит координаты объектов карты и атрибуты в разных таблицах одной БД (Рисунок 4.19), которые связываются механизмом, подобным реляционному соединению [Healey, 1991]. Кроме того, атрибуты могут размещаться в тех же таблицах, что и графика.
Рисунок 4.19. Интегрированная ГИС. Для хранения графики и атрибутов может быть организована единая БД. Существуют два способа хранения координатной информации в реляционных таблицах. В первом записываются отдельные пары координат, представляющие точечные объекты, а также конечные и промежуточные точки линий и границ областей, как индивидуальные атомы, или строки, базы данных. Этот подход удовлетворяет нормальным формам Кодда, но сильно затрудняет поиск, так как каждый графический примитив должен восстанавливаться из атомизированного представления для воссоздания целых полигонов или их групп. Даже при одном только отображении карты выбираются большие группы графических элементов, и эта функция используется чаще, чем пользователи могут думать, просматривая результаты промежуточных шагов анализа. Чтобы избежать этого неудобства, интегрированная модель может записывать в одну колонку таблицы целые цепочки координатной информации. Таким образом, одна область может быть описана одной строкой таблицы, содержащей в одной колонке идентификатор области, а в другой - список идентификаторов линий. Тогда линии, идентифицируемые по этому коду в отдельной колонке таблицы Картографические и геоинформационные структуры данных линий, описывали бы расположение области набором пар координат. Этот подход сокращает расходы на выборку и отображение, но нарушает первую нормальную форму. Обычно с точки зрения пользователя это не является серьезной проблемой, а группировка этих неатомизированных цепочек данных в виде одномерных массивов в одной колонке обеспечивает более высокую производительность системы [Dimmick, 1985] при более строгом выполнении правил первой нормальной формы [Sinha and Waugh, 1988]. Выбор гибридной или интегрированной системы для большинства пользователей вопрос скорее прагматический, чем технический. Каждая имеет свои достоинства, и с переходом к более мощным компьютерам, сетевым технологиям и распределенным вычислениям обе могут дать широкий спектр аналитических возможностей. Для большинства из нас, во всяком случае для новичков, выбор будет сделан другими. Те же, кто находится в более завидном положении самостоятельного выбора, хотят определить, какая из них лучше всего соответствует имеющемуся оборудованию и будущим сетевым потребностям. Оба типа систем совершенствуются, и нужно будет запросить у поставщика подробные спецификации и даже тесты производительности на заданных аппаратных конфигурациях. Помимо двух уже рассмотренных моделей высокого уровня на сцену выходит третья, называемая объектно-ориентированной моделью данных. Эта модель включает язык пространственных запросов [Healy, 1991] и отражает признание того факта, что требуется объектно-ориентированный доступ и к БД ГИС и к выполняемым с ней операциям. Идеи, лежащие в основе этих систем практически идентичны объектно-ориентированному подходу в программировании [Aronson, 1987]. * для полноты следует еще упомянуть и события, которые может порождать объект — прим. перев. Относительно понятия "объектно-ориентированный" не существует общего соглашения, но известно, что "объект" это есть некая сущность, которая имеет состояние, представляемое локальными переменными (этого объекта) и набором операций, которые могут применяться к этому объекту*. Поскольку каждый отдельный объект принадлежит какому-то множеству объектов и операций, его можно рассматривать как член этого класса (т.е. множества, определенного одновременно наборами локальных переменных и операций). Каждый из этих классов наследует свойства от своего надкласса - подобно тому, как люди наследуют характеристики более общего множества, называемого млекопитающими. В случае ГИС для иллюстрации этой идеи можно привести пример класса объектов полигон, который дает каждой области в базе данных все ее свойства (например, списки узлов, дуг и областей; процедуры вычисления центроидов, отображения, наложения полигонов и т.д.) (Рисунок 4.20). 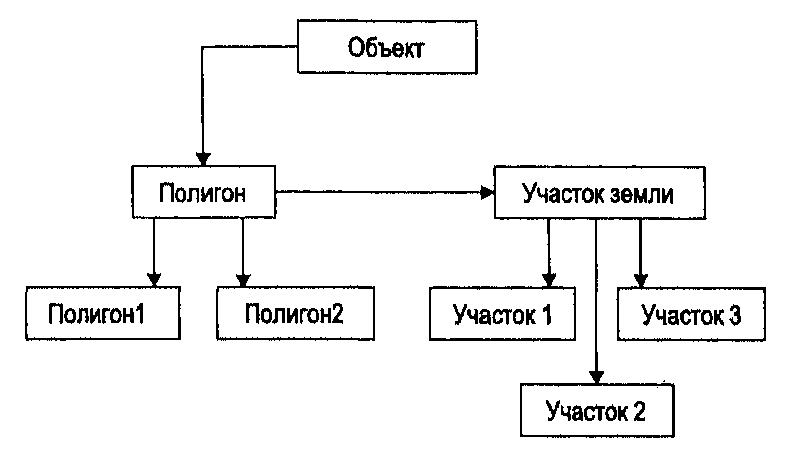 Рисунок 4.20. Объектно-ориентированная ГИС. Пример иерархии классов объектов, как они могли бы быть сконфигурированы в объектно-ориентированной ГИС. Кроме того, в контексте ГИС класс объектов полигон является надклассом по отношению к множеству объектов, называемых участок земли. Таким образом, объекты этого класса наследуют переменные и операции надкласса полигон, а также имеют свои собственные характеристики (например, категория участка, его цена, владелец, процедуры передачи собственности, перезонирования). Эта явная связь переменных и операций, вместе со наследованием свойств, лучше соответствует реальным географическим запросам. Она также обеспечивает метод передачи изменений в одном множестве объектов связанным с ним объектам. Примером объектно-ориентированной ГИС является система INTERGRAPH TIGRIS [Herring, 1987], которая основана на объектно-ориентированном программировании, а не на новых разработках объектно-ориентированных СУБД. Эта технология очевидно проникает в среду ГИС, но пока объектно-ориентированные подходы предлагают лишь некоторые потенциально мощные инструменты географического моделирования и не являются широко доступными для массового потребителя. Недостаточная ориентированность на конечного пользователя не должна отпугивать тех, кто желает с ними поэкспериментировать, особенно если бюджет организации позволяет иметь несколько систем. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
