Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
Рисунок 3.3. Влияние масштаба на точность. Участок карты очень мелкого масштаба, увеличенный до большего масштаба. Линии стали толще и демонстрируют высокую степень генерализации; площади не точны; измерения и анализ практически невозможны. ДРУГИЕ ХАРАКТЕРИСТИКИ КАРТ Карты, как изображения мира, который мы ими моделируем, показывают как положения объектов в пространстве и их форму, так и качественные и количественные их характеристики. Эти взаимосвязанные геометрические объекты и атрибуты (entities and attributes) необходимы для картографического документа. Но независимо от того, какие объекты реального мира представляются этими точками, линиями, площадями или поверхностями, они не могут выступать в качестве миниатюризации действительности из-за ограничений масштаба. Вместо этого мы должны хранить их в памяти компьютера, а затем, при отображении, использовать какой-либо набор символов для их представления. Символы, в свою очередь, должны иметь ключ к их пониманию, называемый легендой карты (map legend). Легенда фактически соединяет геометрические объекты с их атрибутами, после чего каждый из них может быть воспринят в качестве представления реального объекта с его количественными характеристиками. Таким образом читатель карты может представить себе, что же в действительности наблюдалось при сборе исходных данных различными методами, о которых мы уже говорили. Как вы помните из Главы 2, характеристики объектов могут выражаться с использованием различных шкал измерения. С каждым различным типом пространственных данных и каждой шкалой измерения данных связывается определенный набор символов. Мы рассмотрим различные типы пространственных данных и возможности их изображения на карте, виды символов, которые могут их представлять, и то, как картографическое представление ограничивает возможности их использования для ввода в геоинформационную систему. КАРТОГРАФИЧЕСКИЕ ПРОЕКЦИИ Хотя при рассмотрении с близкого расстояния Земля выглядит относительно плоской, мы все знаем, что она имеет приблизительно сферическую форму. Карты, как мы видели, - сокращение реальности, они придуманы для того, чтобы представлять не только объекты на ее поверхности, но и форму Земли. Глобус - традиционный способ отображения формы Земли. Хотя глобусы в целом передают форму Земли и показывают пространственные очертания объектов размером с континент, их довольно трудно носить в кармане, даже при очень мелком масштабе (даже при 1:100'ООО'ООО). Большинство тематических карт, с которыми нам приходится сталкиваться на практике, в географическом анализе, имеют значительно более крупный масштаб, где-то от 1:1'ООО'000 до 1:1000, в зависимости от уровня детализации. Глобус такого размера было бы трудно и дорого делать и еще более трудно переносить или разворачивать на столе дигитайзера (digitizing table) для ввода в ГИС. Поэтому картографы разработали набор методов, называемых картографическими проекциями (mар projections), которые предназначены для изображения с приемлемой точностью сферической Земли на плоском носителе. В буквальном смысле, процесс создания проекции представляется как помещение источника света внутри прозрачного глобуса, на котором размещаются непрозрачные земные объекты, и проецирование их контуров на двухмерную поверхность, окружающую глобус. Возможны разные виды проецирования при окружении глобуса цилиндром, конусом и даже помещении возле него плоского листа бумаги. Каждый из этих методов, как первоначально представлялось, создает так называемое семейство проекций (projection family). Поэтому существуют семейство планарных (planar) проекций, семейство цилиндрических (cylindrical) проекций и семейство конических (conical) проекций (Рисунок 3.4). Существует еще четвертое семейство проекций, называемых азимутальными (azimuthal), они основаны на идее проецирования параллельными лучами света на плоский материал; мы их рассмотрим чуть позже. Сегодня процесс проецирования сферической поверхности на плоский носитель выполняется с использованием методов геометрии и тригонометрии, которые воспроизводят физический процесс проецирования света через глобус. 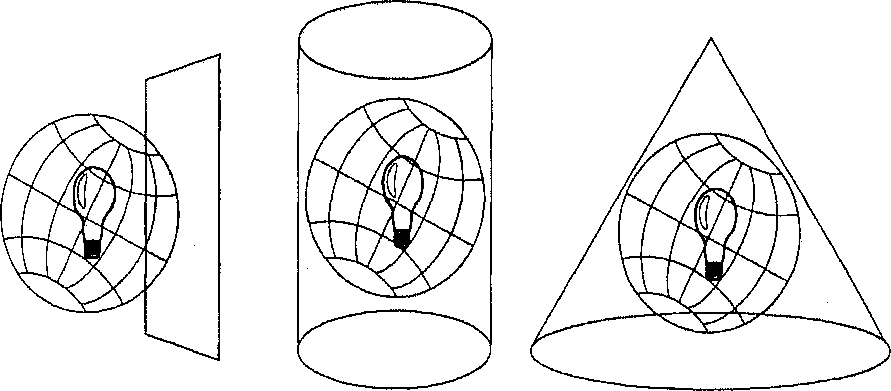 Рисунок 3.4. Три семейства картографических проекций. Они могут создаваться с использованием: а) плоских поверхностей, b) цилиндров, с) конусов. Картографы разработали и другие проекции для лучшего представления Земли на плоском материале. К сожалению, многие из тех в географическом сообществе, кто не является картографом, по большей части пренебрегали этим важным аспектом представления пространства. Причины этому кроются в истории и философии географии. Но с распространением спутникового дистанционного зондирования и географических информационных систем этим вопросом нельзя пренебрегать и дальше. Он тем более значим сегодня, поскольку существует потребность в минимизации искажающих эффектов проекций при представлении пространственных феноменов, плюс широкий спектр картографической информации, с которой географу каждый день приходится иметь дело за компьютером. Эти вопросы оказывают воздействие на все подсистемы ГИС и должны быть хорошо поняты, дабы ограничить их негативное влияние. Проекции - не абсолютно точные представления географического пространства. Каждая создает свой набор типов и величин искажений на карте. Важные характеристики карт, которые должны сохраняться для точных аналитических операций, часто определяют выбор той или иной проекции. Эти характеристики включают углы (или формы), расстояния, направления, площади объектов. При выполнении проекции невозможно сохранить все эти характеристики одновременно. Мы рассмотрим каждую из них в отдельности, но сначала нам нужно установить некоторую полезную терминологию, помогающую нам понимать изменения характеристик в процессе проецирования. Упрощенно, процесс проецирования представляется двумя этапами: вначале преобразуют земной шар в промежуточный глобус (reference globe) в зависимости от выбранного масштаба; затем этот глобус проецируется на плоскую поверхность [Robinson et al., 1995]. Численный масштаб первого преобразования называется главным, или общим, масштабом (principal scale), он равен отношению радиуса промежуточного глобуса к радиусу земного шара. Таким образом мы имеем численный масштаб, постоянный по всей поверхности этого глобуса, поскольку его форма повторяет форму земного шара. Перед тем, как сделать второй шаг, отметим, что масштабный коэффициент (scale factor), называемый также относительным масштабом, определяемый как частное отделения местного масштаба (actual scale) на общий масштаб, по определению равен единице по всей поверхности промежуточного глобуса. Когда же мы переходим от его сферической поверхности к двухмерной карте, относительный масштаб обязательно изменится, поскольку плоская и сферическая поверхности не совместимы. Следовательно, масштабный коэффициент будет разным в разных точках карты [Robinson et al., 1995]. Нам нужно постоянно помнить об изменяющемся масштабном коэффициенте, когда мы рассматриваем различные виды искажений, возникающих при проецировании. На поверхности глобуса направления сторон света всегда отстоят от соседних на 90°. То есть, например, между севером и востоком всегда прямой угол. Это соотношение углов может сохраняться и на картографической проекции. Проекции, сохраняющие это свойство углового соответствия (angular conformity), называются конформными, или равноугольными (conformal, orthomorphic), картографическими проекциями. Конформные проекции позволяют нам математически организовать сжатия и растяжения на карте так, чтобы масштабный коэффициент не зависел от направления в каждой ее точке. При этом масштабный коэффициент не будет равен единице в каждой точке карты, а параллели и меридианы в полученной карте всегда будут проходить под прямыми углами друг к другу, как они и были на глобусе, однако площади объектов будут искажены [Robinson et al., 1995]. Запомните, что сохранение углов труднодостижимо для больших участков земной поверхности и этого разумно добиваться лишь для малых участков. Конформные проекции искажают площади, что делает измерения площадей на карте некорректными. Но мы можем сохранить площади, используя равновеликие, или равноплощадные, проекции (equal area or equivalent projections), в которых произведение масштабных коэффициентов по главным направлениям горизонта равно единице [Robinson et al., 1995]. Это условие гарантирует, что если вы, например, считаете площади квадратных объектов на карте, то произведение их двух сторон даст тот же результат, что и при подсчете на промежуточном глобусе. Это обусловлено тем, что произведение масштабных коэффициентов по этим двум направлениям равно единице. Однако, при достижении этой идентичности мы обнаруживаем, что масштабный коэффициент будет разным по разным направлениям для всех точек карты, кроме точек, лежащих на особых линиях проекции. Другими словами, сохраняя площади, мы искажаем углы. Таково фундаментальное соотношение этих двух параметров для проецированных карт - нельзя одновременно сохранять и площади и углы. Если целью проецирования карты является измерение расстояний, то нам следует выбрать проекцию, сохраняющую расстояния. Такие проекции, называемые равнопромежуточными, или эквидистантными (equidistant projections), требуют сохранения масштаба карты постоянным; он должен быть таким же, как и главный масштаб промежуточного глобуса [Robinson et al., 1995]. Существуют два способа добиться этого. Первый сохраняет масштабный коэффициент равным единице вдоль одной или более параллельных линий, называемых стандартными параллелями (standard parallels). Расстояния, измеренные вдоль этих линий, будут соответствовать реальным. Другой подход заключается в сохранении единичного масштабного коэффициента вдоль всех направлений из одной точки, либо из двух. Расстояния, измеренные от таких точек по любому направлению, будут точно представлять реальные. Но для любых других точек это не будет соблюдаться. Как вы понимаете, здесь очень важен выбор таких точек. Обычно выбирается та точка, от которой производится большинство измерений. Когда карты используются для навигации, наибольший интерес представляет сохранение направлений. Сохранение истинных направлений ограничено сохранением дуг окружностей больших кругов, которые определяют кратчайшее расстояния между двумя точками на поверхности Земли. Обычно нашей целью является отображение маршрутов этих больших кругов как прямых линий. Есть два основных способа сделать это. Первый используется для малых областей, в которых большие круги отображаются практически прямыми линиями между всеми точками области. Однако, если вы пересекаете с ними меридиан, то угол пересечения будет неправильным. Как ограниченная площадь, так и неточность углов пересечения меридианов и больших кругов, существенно ограничивают использование этой проекции для данных целей. Альтернативный вариант, называемый азимутальной проекцией, более широко используется для сохранения направлений. Как и в случае эквидистантной проекции мы выбираем одну или две точки, из которых будут сохраняться направления. В этом случае прямые линии, проведенные из этих точек, будут соответствовать истинным направлениям. Опять же, направления из любых других точек не будут соответствовать реальности. Позднее мы обсудим проблему смешивания разных проекций внутри одной геоинформационной системы, особенно при вводе, но пока нам нужны некоторые практические правила для определения того, какие из множества картографических проекций нам подошли бы в зависимости от видов выполняемого анализа. Если анализ требует отслеживания движения или изменения направлений движения объектов, например, при использовании телеметрии для регистрации положений каждого члена стада северных оленей в разное время, то наиболее подходящей будет конформная проекция. Этот вид проекций также больше всего подходит для производства навигационных карт и когда важна угловая ориентация, как часто бывает с метеорологическими или топографическими данными, Эта группа проекций включает проекции Меркатора, поперечную Меркатора, коническую конформную Ламберта и конформную стереографическую. Общегеографические и учебные карты чаще всего требуют использования равновеликих проекций, но наш интерес — анализ. Как говорит название, такие карты больше всего подходят, когда среди вычислений преобладают вычисления площади. Например, если вы заняты расчетом изменения соотношений разных видов растительного покрытия земли со временем, или если вы исследуете некоторую местность на предмет достаточной площади для размещения торгового комплекса, то равновеликие проекции подойдут лучше других. Рассматривая использование равновеликих проекций, вам необходимо учитывать размер интересующей территории, а также величину и распределение угловых искажений. Небольшие участки отображаются с гораздо меньшими угловыми искажениями при использовании равновеликих проекций, что может быть полезно, когда важны и площади и формы. С другой стороны, чем больше площадь изучаемой территории, тем более точны ее измерения при использовании равновеликой проекции, по сравнению с проекциями других типов. Для среднемасштабных карт наиболее часто встречаются равновеликая проекция Альберта и равновеликая проекция Ламберта. Проекты, в которых требуется определение кратчайших маршрутов, особенно на длинные дистанции, нуждаются в азимутальных проекциях, поскольку в них возможно изображение больших кругов как прямых линий. Эти проекции чаще всего используются на картах воздушного сообщения, радиопеленгации, слежения за спутниками и картографирования других небесных тел [Robinson et al., 1995]. Эти проекции стали популярны лишь недавно, но их использование будет расти с расширением использования ГИС в этих областях. Наиболее часто вам будут встречаться такие азимутальные проекции как равновеликая Ламберта, стереографическая, азимутальная эквидистантная, ортографическая и гномоническая проекции. Отметим, что некоторые из них сохраняют как направления, так и площади. Это свойство может оказаться полезным для анализа крупных атмосферных явлений, таких как дымовые следы вулкана, которым свойственно двигаться по маршруту большого круга по мере рассеивания в атмосфере и движения по общим правилам циркуляции на Земле. Есть много проекций для выбора — гораздо больше, чем перечислено здесь. Некоторые специальные проекции особенно подходят для отображения всей Земли или очень больших ее участков. Другие позволяют лучше координировать крупные картографические программы, такие как создание топографических карт целого континента, которое выполняется небольшими порциями. Список велик. Как вы увидите позднее, выбор проекции - один из основных процессов создания ГИС. Вам следует потратить время на выбор хорошего справочника по картографическим проекциям, с особым вниманием к тому, какие параметры каждая из них сохраняет. С нашей точки зрения могут оказаться полезными две книги: [Nyergesand Jankowski, 1989] и хорошо известный справочник [Snyder, 1988; есть более современное издание]. СИСТЕМЫ КООРДИНАТ ДЛЯ КАРТОГРАФИИ Система координат необходима для определения расстояний и направлений на земле. Географическая система координат, использующая широту и долготу, хороша для определения положений объектов, расположенных на сферической поверхности Земли или промежуточном глобусе (reference globe). Поскольку чаще всего мы будем иметь дело с двухмерными картами, спроецированными с этого глобуса, нам потребуется одна или несколько систем координат, соответствующих различным проекциям. Такие системы координат на плоскости называются картографическими (геодезическими) прямоугольными системами координат, они позволяют нам точно указывать положение объектов на плоских картах.  Рисунок 3.5. Декартова система координат. Классическая система прямоугольных координат. Каждая точка определяется парой величин — координатой X (абсциссой) и координатой Y (ординатой). Основная система прямоугольных координат знакома вам по работе с графиками и числовыми осями. Она состоит из двух линий - абсциссы и ординаты. Абсцисса - горизонтальная линия, содержащая равномерно распределенные числа начиная с 0, называемого началом координат, и продолжающаяся так далеко в двух направлениях, насколько это нам нужно для измерения расстояний (Рисунок 3.5). Величины называются X-координатами, они положительны справа от 0 и отрицательны слева. Вторая линия, ордината, обеспечивает нам движение по вертикали от той же начальной точки в положительном или отрицательном направлении. Вместе они позволяют нам определять местоположение любой точки или объекта указанием величин X и Y. Как вы увидите позднее, дигитайзеры (digitizers), устройства, используемые для ввода координат в ГИС, основаны на той же простой декартовой системе координат (Cartesian coordinate system). По традиции, первой называют координату X, второй - Y. Когда карта ориентирована севером вверх, как обычно, Х-координата называется отсчетом на восток (easting), поскольку он соответствует расстоянию от начальной точки в восточном направлении. Аналогично, Y-координата называется отсчетом на север (northing), поскольку он соответствует расстоянию на север от начальной точки*. Как вы можете заметить, нет западного или южного указаний. Вместо этого начальную точку размещают на карте так, чтобы все значения были положительны, или, иначе говоря, чтобы все точки оказались в северо-восточном квадранте системы координат. Это позволяет нам читать координаты сначала вправо, затем вверх от начальной точки. В некоторых случаях размер территории может потребовать от нас введения смещенных (ненулевых) начал координат (false origins), чтобы обеспечить для каждого участка земли достаточно точное представление на плоской поверхности. Как указывалось, численные значения плоских координат обычно не используются в анализе мелкомасштабных карт из-за сложного характера искажений. Для таких карт требуется компенсация искажений, созданных при проецировании. Несмотря на большое количество имеющихся проекций, подавляющее большинство систем координат на плоскости пытаются достичь равноугольности использованием только равноугольных картографических проекций, обычно поперечной Меркатора, полярной стереографической и равноугольной конической Ламберта. Хотя, так бывает не всегда. Например, если область вашего интереса находится вблизи экватора, более полезной может оказаться проекция Меркатора [Robinson et al., 1995]. В США используются пять основных координатных систем, одни из которых основаны на свойствах картографических проекций, другие - на исторических методах деления земли. Если вы работаете с картами других стран, вам нужно установить, каковы проекции, набор координат и другие характеристики координатных систем в этих странах. Во многих странах используются те или другие из перечисленных ниже типов, но перед вводом в ГИС от вас потребуется знакомство с их положениями начал координат и территориями, на которых они используются. * Как уже упоминалось, в России распространена система координат 1942 г. для проекции Гаусса-Крюгера, в которой ось X указывает на север, а ось Y - на восток. ** Это замечание актуально прежде всего для США, где до сих пор преобладают старые английские меры (дюймы, футы, ярды, мили и т.д.), причем эти меры по разному соотносятся Пожалуй, наиболее широко распространенной в ГИС системой проекций и координат является универсальная поперечная Меркатора (universal transverse Mercator (UTM)) (Рисунок 3.6). Она используется в большинстве работ с дистанционным зондированием, подготовке топографических карт, построении баз данных природных ресурсов, так как она обеспечивает точные измерения в метрической системе, принятой в большинстве стран и научным сообществом в целом. В ней основной единицей измерения длины является метр**. UTM делит земную поверхность на 60 пронумерованных вертикальных зон шириной по шесть градусов долготы, каждая из которых проходит от 80-го градуса южной широты до 84-го градуса северной широты. Чтобы все координаты были положительными, в UTM есть два начала ординат: одно - на экваторе (для северного полушария), другое - на 80-й параллели южной широты (используется для южного полушария). Эти зоны пронумерованы начиная от 180-градусного меридиана в восточном направлении. Земная поверхность делится также на ряды по 8 градусов широты каждый, за исключением самого северного, который составляет 12 градусов, позволяя тем самым покрыть всю сушу северного полушария.  Рисунок 3.6. Универсальная поперечная координатная система Меркатора (UTM). с метром в зависимости от области применения (различаются, например, мили: морская и сухопутная, футы: простой, американский геодезический, модифицированный американский, Кларка, индейский, и т.д.). — прим. перев. Карта как модель географических данных: язык пространственного мышления Каждая секция, образованная пересечением зоны и ряда, обозначается комбинацией числа и буквы (как и раньше, читаем вправо-вверх), поэтому мы можем выделить довольно малые участки земного шара. За исключением самого северного ряда, каждая из таких секций имеет сторону около 100 км, поэтому, для измерений с точностью до одного метра достаточно использовать отсчеты на север и восток из пяти десятичных знаков. Как следует из названия, UTM использует поперечную проекцию Меркатора. Для каждой из 60-ти зон по долготе применяется отдельная реализация проекции с целью уменьшения искажений. Начало координат помещается в центре каждой зоны, на пересечении центрального меридиана зоны с экватором, причем нулевое значение по абсциссе смещено от него на 3 градуса к западу. Масштабный коэффициент 0.99960 не изменяется в направлении юг-север. Однако, он меняется в направлении запад-восток, но даже на самом краю шестиградусной зоны он практически тот же -1.00158. Эта почти полная эквивалентность иллюстрирует малость искажений, свойственную UTM, которая обеспечивает точности, приближающиеся к одному метру отклонения на каждые 2500 м расстояния [Robinson et al., 1995]. Для полярных регионов, лежащих за пределами территории, покрытой координатной системой UTM, но с такой же точностью, используется универсальная полярная стереографическая (universal polar stereographic (UPS)) проекция. Эта система делит полярные регионы на концентрические зоны, затем режет каждую на две половины по меридианам 0 и 180 градусов. Эти половины зон по-разному обозначаются для северного и южного полушарий. В северном полушарии западная половина обозначается как зона Y, восточная — как зона Z. В южном полушарии западная половина обозначается как зона А, восточная — В. Как и в случае с UTM, отсчеты даются на восток и север вплоть до 2000 км. И так же, как в UTM, зоны могут быть поделены на квадраты по 100 км, каждый - со своей собственной реализацией проекции, обеспечивая точность примерно до одного метра на 2500 м. Совместно UTM и UPS обеспечивают покрытие всего земного шара с очень малыми искажениями и весьма точными измерениями. КАРТОГРАФИЧЕСКИЙ ПРОЦЕСС Помимо определения масштаба, проекции и системы координат, ГИС-аналитик должен знать и об основных этапах процесса изготовления карты, особенно с точки зрения изменения парадигмы от одного лишь сообщения к сообщению и анализу Имеется четыре основных этапа в картографическом процессе: сбор данных, компиляция данных, создание карты, ее тиражирование. Мы рассматривали сбор данных как первый наш шаг в формализации концептуальной модели пространства. А в Главе 14 мы займемся производством и тиражированием как процессами, присущими фазе выхода документов из ГИС. Но фаза компиляции данных в картографическом процессе должна быть тщательно рассмотрена здесь, перед тем, как мы рассмотрим структуры данных в Главе 4 и ввод данных в Главе 5. По традиции процесс картографической компиляции данных включает в себя выбор или разработку базовой карты (base map), на которой размещаются собранные данные. Для представления точек, линий, площадей и поверхностей используются наборы символов, каждый из которых может сдвигаться относительно своего точного положения, чтобы дать место другим на ограниченной поверхности карты. Для группирования данных статистическими методами используются процессы предварительного отбора и сортировки. В рамках парадигмы сообщения группирование чаще всего выполнялось как отдельный шаг или набор операций до начала процесса создания собственно карты. С продвижением аналитической парадигмы группирование стало выполняться в рамках ГИС с применением методов статистики и управления базами данных. Однако циклическая природа функционирования ГИС (см. Главу 13) маскирует группирование как легко опознаваемую часть картографического процесса. Тем не менее, многие карты, включаемые в базу данных ГИС, создавались при традиционной парадигме сообщения. И как мы уже видели, процесс компиляции может не сохранять исходные данные, поскольку создаются классификации, основанные на первоначальных критериях разработки карты, оставляя ГИС-аналитикабез полного набора атрибутивных данных, которые можно было бы ввести в ГИС. КАРТОГРАФИЧЕСКИЕ СИМВОЛЫ В последнем разделе мы обсудим проблемы, связанные с компьютерным представлением данных, особенно те, что связаны с процессом ввода существующих картографических документов. Но вначале более полезным будет краткий обзор некоторых базовых концепций компиляции данных, которые и создают эти картографические документы. Эти концепции пригодятся и позже, когда мы займемся выводом документов из ГИС, поскольку тогда мы вернемся к картографической компоновке в рамках компьютеризованной среды. Как мы уже видели, карты не являются точными уменьшенными копиями реальности, а ее представлением. Мы видели, что географические объекты оказываются точками, линиями, областями и поверхностями, и мы видели также, что их характеристики могут быть описаны с применением четырех различных шкал измерений. Когда мы переходим к картографическому изображению, нам нужно представлять все эти объекты независимо от шкалы измерений тщательным отбором, классификацией и символизацией так, чтобы результаты физически уместились бы на выделенной площади и пользователь смог бы понять, что здесь представлено. Ранее мы использовали Рисунок 2.4 для иллюстрации связи между типами пространственных данных и их шкалами измерения [Muehrcke and Muehrcke, 1992]. Как вы можете помните, у нас есть некоторые наборы символов, соответствующих точкам, линиям, областям и поверхностям на всех шкалах измерения. Рисунок 2.4 объединял последние две шкалы как интервал/ отношение, поскольку для них набор символов обычно один, вместо того, чтобы рассматривать их раздельно. Это важно отметить, так как это создает еще один уровень представления. Если мы не знаем, как данные первоначально собирались, мы не знаем, являются они интервальными или порядковыми. Символы этого не показывают. Мы можем выполнить операции шкалы отношений на наборе данных, который не имеет абсолютной начальной точки отсчета, а результаты такого анализа могут оказаться бессмысленными. Следует заметить также, что поверхности могут изображаться с помощью линий. Это может внести некоторую путаницу, по двум причинам. Первая: новичкам обычно свойственно ошибочно принимать линии за одномерные объекты, а не способ отображения поверхностей. Это легко преодолевается постепенным знакомством со свойствами карт и символов на все большем количестве картографических документов. Вторая проблема состоит в принятии самих линий за точные представления значений высот точек (см. Главу 2). Как мы видели, линии - это оценки или предположения о точных значениях высоты, сделанные в результате интерполяции. Хотя эти линии могут быть хорошими приближениями высот, изучающему геоинформатику следует помнить об их предположительной природе, особенно если они используются при вводе в ГИС. Единственными не предположительными значениями высот являются те, что были действительно измерены, что показывается отметками высот на топографических картах. Как вы позднее увидите, большинство коммерческих ГИС имеют свои собственные интерполяционные возможности. И уже вашим делом будет решать, вводить ли только местоположения известных точек, или сами линии, зная характеристики и надежность применяемых методов интерполяции (см. Главу 5). Использование линий для представления поверхностей - только один пример из многих по изменению пространственной мерности, которое может происходить в результате представления информации при помощи символов. Рисунок 1.1 показывает различные примеры соотношений мерности объектов и изображающих их символов, которые могут присутствовать на карте. Здравое рассуждение всегда необходимо при решении, является ли геометрия и мерность символа точным представлением объекта. Например, если для изображения точечного объекта используется площадной символ, вам нужно помнить, что несмотря на его двухмерность, вводиться в компьютер или иначе регистрироваться должна лишь одна точка. То же самое можно сказать и о шкалах измерения. Символы, такие как кружки градуированного диаметра, используемые для точечных объектов, часто изменяются для достижения определенного визуального эффекта [Robinson et al., 1995]. Такое изменение размера символа не прямо пропорционально изменению значения данных, оно рассчитано скорее на визуальное восприятие пропорциональности зрителем. Такие манипуляции обычны в картографии, поэтому специалисту по ГИС следует тщательно рассмотреть карту перед тем, как выполнять кодирование данных на основе изменений символов. Как всегда, если есть доступ к исходным данным карты, атрибуты должны браться из них, а не из их графического представления. Главным различием между парадигмами сообщения и аналитической является манипуляция с данными до создания карты в целях классификации. Поскольку одна тематическая карта служит одной цели, обычно процесс классификации происходит лишь однажды, а исходные данные пользователю карты уже не доступны. Рассмотрим случай choropleth или value-by-area карт. В случае парадигмы сообщения мы хотим сгруппировать области в осмысленные и визуально привлекательные агрегации. Многочисленные методы группирования (агрегирования) таких областей вместе называются выбором интервалов классификации (class interval selection). Среди этих методов есть несколько достойных внимания групп. К первой группе методов мы отнесем такие, в которых весь диапазон значений разбивается на некоторое число равных интервалов. Вторая группа методов классификации использует переменные интервалы. Они создают несколько более сложные для восприятия карты, но могут быть очень полезны для выделения определенных экстремальных значений или подчеркивания вариаций величины. Переменные интервалы могут быть систематическими, включая арифметические, логарифмические и другие ряды; или они могут быть несистематическими, с объединением данных в естественные группы, которые и являются критерием выбора интервалов классификации. Третью группу методов составляют такие, в которых в каждую категорию попадает одно и то же количество объектов (интервалы равного наполнения). Эти методы можно рассматривать как особую группу среди методов переменных интервалов. Каждый из этих методов имеет свои особенности. Одни производят хорошо сбалансированную карту (см. Главу 14), другие более просты, третьи обеспечивают наличие данных в каждом классе. Все эти методы выбора интервалов классификации могут применяться по отношению к точечным, линейным и площадным символам для отображения всех типов пространственных данных. Возьмем для примера использование интервалов между горизонталями на топографических картах. Выбор этих интервалов - в такой же степени метод выбора интервалов классификации, как и группировка областей для choropleth карт. Подобным же образом, создание дискретного набора точечных символов для отображения различий значения атрибута является методом выбора интервалов классификации, поскольку известно, что человеческий глаз не способен заметить очень малые отличия в размере Все эти методы выбора интервалов создают картографические документы, которые в большей или меньшей степени скрывают исходные данные и при неудачном выборе могут исказить картины исходных распределений. Нам нужно помнить об этих особенностях, когда мы готовим вывод документов из ГИС. С другой стороны, если мы намереваемся использовать эти классифицированные карты для ввода в базу данных ГИС, мы должны быть очень осторожны при выполнении анализа с этими в значительной степени обработанными данными. Конечно, символизация и классификация - не единственные методы картографической компиляции, о которых нам нужно знать. Среди наиболее важных процессов компиляции, с которыми придется встретиться специалисту по ГИС, находится графическое упрощение. Производимое этим процессом сокращение объема данных следует учитывать при вводе карт в ГИС, оно также оказывает влияние на результаты последующих измерений и анализа. Упрощение удаляет некоторые нежелательные объекты, сглаживает, агрегирует или иначе модифицирует объекты на карте. Мы встречали пример этого в предшествующем рассмотрении изменений мерности. Конечной целью упрощения является обеспечение читабельности картографического документа. Здесь используются два основных метода: удаление и сглаживание объектов. Рассмотрим их по отдельности. При удалении объектов мы выполняем функцию, которая очень похожа на сам процесс сбора пространственных данных (Рисунок 3.9) [Muehrcke and Muehrcke, 1992]. Наши наблюдения проходят через наш "географический фильтр", оказывающий влияние на решения о том, что мы зафиксируем, а что - проигнорируем. Важность объектов определяется еще до начала сбора данных и определяется главным образом его целями. В действительности, отбор объектов для рассмотрения будет неявным эквивалентом процесса удаления объектов с карты, поскольку только зарегистрированные во время сбора данных объекты будут помещены в базу данных картографического документа. Конечно, в некоторых случаях нерегистрация объектов происходит из-за того, что мы не можем их наблюдать в полевых условиях с имеющимся инструментарием. Возможность регистрации объектов является также функцией состояния научного знания и регистрирующей техники на момент сбора данных. Например, изменения в растительных и животных видах влияют на результаты переписи; местоположения млекопитающих, которые раньше не могли быть зафиксированы конкретно, теперь могут регистрироваться с помощью радиотелеметрии; мы не могли собирать широкомасштабную информацию об изменениях населения и социоэкономических показателях до начала общенациональной переписи. Чувствительность к факторам окружающей среды и их взаимодействиям определяет наше представление о них, что, в свою очередь, определяет то, что мы выбираем для исследования и дальнейшего нанесения на карту, а что устраняем. 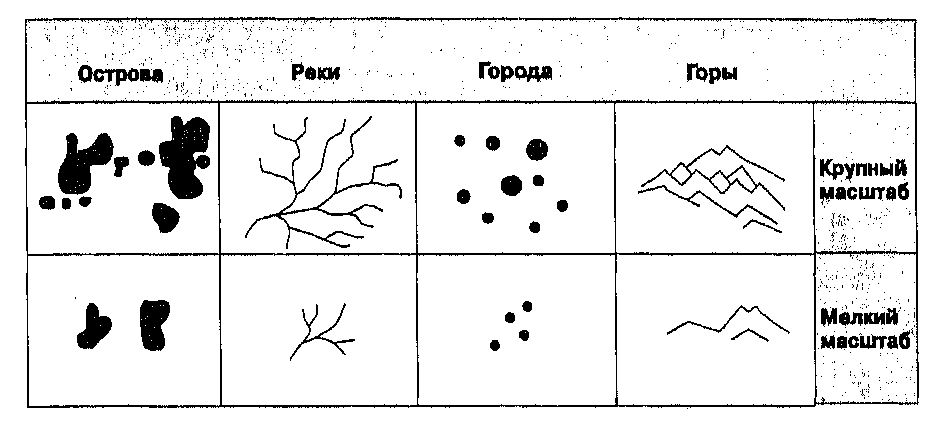 Рисунок 3.9. Изменение масштаба и исчезновение объектов. Сравнение точечных, линейных, площадных и поверхностных объектов, видимых на крупномасштабной карте и исчезающих на мелкомасштабной. В отличие от пассивного, обусловленного возможностями сбора данных, активное удаление объектов может использоваться как при сборе данных, так и при создании карты, а также при разработке картографической базы данных. Схемы отбора (sampling schemes), которые мы прежде рассматривали, являются ярким примером устранения больших частей информации об объектах, которая могла бы быть собрана. Мы также проводим активное удаление объектов на карте или в самой цифровой базе данных перед завершением создания карты. Здесь как ограничитель действует Карта как модель географических данных: язык пространственного мышления скорее карта, нежели человек, собирающий информацию. Мелкие населенные пункты часто не показываются на картах плотно заселенных областей, однако населенные пункты такого же размера могут появляться на картах областей с низкой плотностью населения. Аналогично, мы можем удалять некоторые мелкие или менее значительные притоки рек, озера или острова во время картографического процесса из-за недостатка места на карте. Эта генерализация может быть такой простой, как исключение определенной части объектов, например, каждого второго; или она может включать набор правил (например, исключение населенных пунктов с количеством жителей меньше определенного числа, удаление наиболее мелких притоков в речной сети). Какой бы набор методов ни применялся, результатом будет менее детальная карта. Очевидно, что если в геоинформационную систему вводятся данные, прошедшие процедуру упрощения, вы получите картографическую БД с отсутствием некоторых данных. 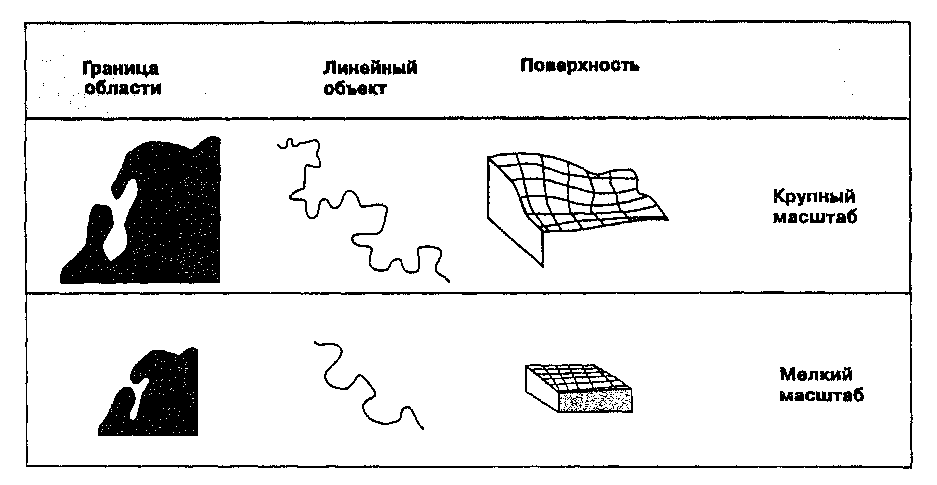 Рисунок 3.10. Изменение масштаба и сглаживание. Заметьте, как объекты упрощаются до сохранения только наиболее представительных характеристик. Другой полезный метод упрощения называется сглаживанием (Рисунок 3.10). Этот процесс превращает детализированные геометрические объекты в менее детализированные. Подобно шаржам на известные личности, важные геометрические характеристики сохраняются в виде упрощенных геометрических форм. На картах, показывающих прибрежные районы, границы, извилистые реки или острова, мы можем упрощать линии, представляющие эти нерегулярные объекты, так, чтобы их существование |
