Майкл ДМерс ГИС. Инициаторы проведения этого новаторского события надеются привлечь к нему внимание мировой общественности и широких масс пользователей географических информационных систем из всех стран.
 Скачать 4.47 Mb. Скачать 4.47 Mb.
|
|
Глава 4 разделением всего массива записей на две половины и выборкой записи в середине. Если она оказывается той, что нужна, то процедура поиска закончена. Если искомая запись находится прежде выбранной, то мы выполняем ту же операцию с первой половиной, если после - со второй.  Рисунок 4.3. Последовательно упорядоченный файл. Иллюстрация структуры файла как упорядоченной картотеки. В данном случае сортировка производится с использованием алфавита. Таким образом, программе не требуется просматривать большую часть файла. Среднее количество операций в этой стратегии определяется как log2(n+l). В нашем прежнем примере время поиска сокращается до немногим более двух часов вместо прежних 28-ми. Конечно, любой компьютер, которому требуется целая секунда для выполнения одной операции, скорее всего не подойдет для ГИС. Но пропорциональный выигрыш во времени из данного примера вполне очевиден. Однако, скорость поиска не достается бесплатно, поскольку теперь каждая новая запись должна вставляться в соответствующее место последовательности, иначе ваш файл быстро превратится в неупорядоченный, который уже потребует последовательного перебора записей. Индексированные файлы В обоих предыдущих примерах записи идентифицировались и сравнивались по ключевому атрибуту - слову или числу. Стратегия поиска была основана на значениях самих ключевых атрибутов. Элементы, которые вы ищете в ГИС, это главным образом точки, линии и области. Однако вряд ли вы будете искать их по присвоенным им номерам. Другими словами, вы не будете запрашивать ГИС отобразить линию номер 3001 (ее порядковый номер при вводе в систему). Каждому объекту даются некие описательные атрибуты (характеристики), поэтому чаще всего ищутся элементы с определенным набором атрибутов. Так, например, вы могли бы попросить ГИС отыскать для отображения и анализа все земельные участки в отличном состоянии. Или вы могли бы выбрать участки в плохом состоянии, причем такие, у которых уклон меньше 25%. Каждому объекту может быть приписано большое количество атрибутов, но мы физически не можем отсортировать записи в файле одновременно более чем одним способом. И если для того атрибута, по которому мы отсортировали массив записей, мы можем применить быстрый поиск делением пополам, то для всех других атрибутов нам придется выполнять утомительный последовательный поиск. Нам нужен какой-то выход, ведь мы же не можем пересортировывать файл для каждого запроса! Решение для этого существует - внешний индекс. Строится он вот как: из исходного файла в новый файл копируются значения одного атрибута для всех записей вместе с положениями этих записей. То есть каждая запись в новом файле состоит из значения атрибута и адреса записи в исходном файле, из которой это значение было взято. Затем нужно упорядочить записи нового файла в соответствии со значениями атрибута. Теперь, чтобы найти запись с заданным значением атрибута, мы можем в новом файле использовать поиск делением пополам. Найдя нужные записи в индексном файле, мы получим адреса записей исходного файла, по которым можем получить все атрибуты объектов. Таким образом, для поиска в основном файле используется дополнительный индексный файл, который называется внешним индексом, а сам исходный файл, таким образом, стал индексированным. Очевидно, что мы можем выносить в индексный файл несколько атрибутов, чтобы организовывать поиск сразу по значениям этих нескольких атрибутов. Использование внешнего индекса имеет три условия. Во-первых, вам нужно знать заранее критерии, по которым будет производиться поиск: для каждого критерия строится свой индексный файл. Во-вторых, ссылки на все добавления в исходный файл должны помещаться в соответствующие места индексных файлов, чтобы не нарушать их упорядоченность. В-третьих, если вы по какой-либо причине не предусмотрите некоторый критерий поиска, то вам придется использовать последовательный перебор для получения нужной информации. Мы еще коснемся этой темы в Главе 15, посвященной проектированию. 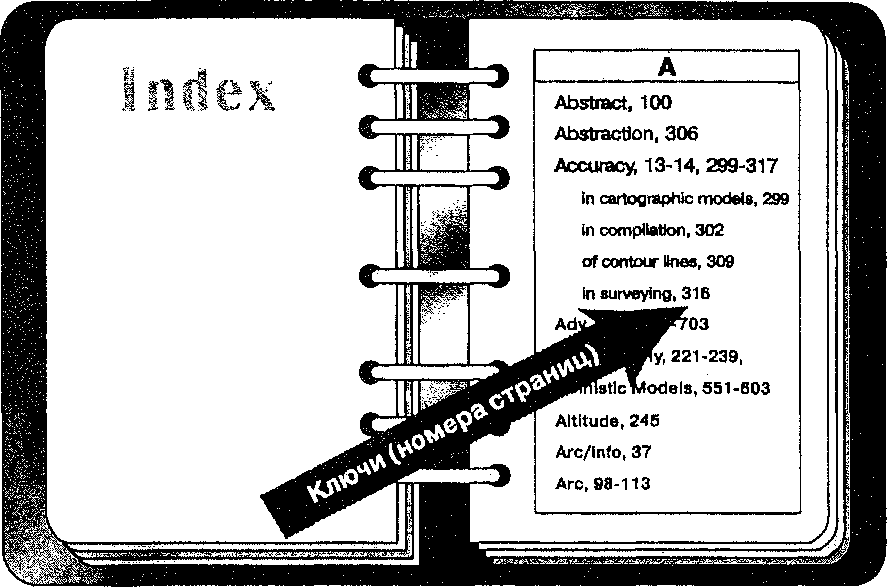 Рисунок 4.4. Индексированная структура данных. В качестве примера индексированного файла - указатель книги, который показывает, как найти информацию в большем файле с помощью ключевой характеристики. СТРУКТУРЫ БАЗ ДАННЫХ ДЛЯ УПРАВЛЕНИЯ ДАННЫМИ Мы редко ограничиваемся одним файлом, обычно мы собираем и используем многие файлы. Организованный набор взаимосвязанных файлов данных называется базой данных. Сложность работы со множественными файлами в базе данных требует более совершенного управления, реализуемого системой управления базой данных (СУБД). Хотя постоянно создаются всё новые реализации структур баз данных, существует всего три основных типа, с которыми вам нужно познакомиться, это иерархическая (древовидная), сетевая и реляционная (табличная) структуры баз данных. Рассмотрим их по отдельности. 
Иерархическая структура данных Например, животные делятся на позвоночные и беспозвоночные. В свою 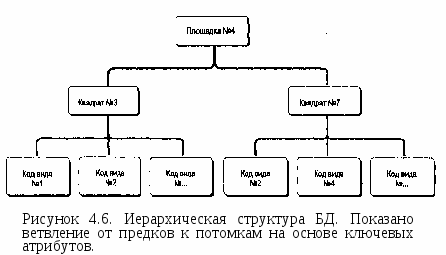 Во многих случаях существует взаимосвязь между данными, называемая отношением "один ко многим" [Burrough, 1983]. Это отношение подразумевает, что каждый элемент данных имеет прямую связь с некоторым числом так называемых "потомков", и, конечно каждый такой потомок, в свою очередь, может иметь связь со своими потомками и т.д. Как следует из названия, предки и потомки напрямую связаны между собой, что делает доступ к данным простым и эффективным (Рисунок 4.6). Такая система хорошо иллюстрируется иерархической системой классификации растений и животных, называемой таксономией. очередь, позвоночные имеют подмножество, называемое млекопитающими. Млекопитающие могут быть далее разделены на подгруппы. Структура становится похожей на генеалогическое дерево, и в действительности таксономисты используют почти такую же графическую форму для представления отношений между видами. Главной характеристикой иерархической структуры, иллюстрируемой таксономическим деревом, является прямая взаимосвязь между одной ветвью и другой. Ветвление основано на формальных ключевых признаках, которые определяют продвижение по этой структуре от одной ветви к другой. Как вы могли догадаться, если ваша информация о ключевом признаке недостаточна, то вы не сможете продвигаться по дереву. В действительности, природа иерархической системы требует явного определения каждого, отношения для того, чтобы создать саму структуру и ее правила ветвления. Главным преимуществом такой системы является то, что в ней очень легко искать, поскольку она хорошо определена и может относительно легко расширяться добавлением новых ветвей и формулированием новых правил ветвления. Но если ваше изначальное описание структуры неполно или если вы хотите двигаться по ней на основе корректного критерия, который не включен в структуру, то поиск становится невозможным. Для создания иерархической структуры совершенно необходимо знание всех возможных вопросов, которые могут задаваться, поскольку эти вопросы используются как основа для разработки правил ветвления или ключей. Наверняка многие из вас сталкивались с компьютерной системой библиографического поиска. Такие системы имитируют способы поиска книг и статей, который люди использовали до внедрения компьютеров. Мы можем искать отталкиваясь от темы, имени автора, названия и даже по диапазону номеров в каталоге, ограничивающем нас частью библиотечного фонда. Системы, которые могут выполнять поиск по множественным критериям и с применением булевых операций отражают обе потребности легкой разработки иерархии - хорошо определенные критерии и ограниченное число типов запросов. Но представьте себе, что вам попадалась хорошая книга по геоинформатике в северо-западном углу пятого этажа главной библиотеки института. Вы не помните номер по каталогу, но хотели бы найти и другие книги, находящиеся рядом с упомянутой. Конечно, вы не будете просить библиографическую систему отыскать все книги в северо-западном углу пятого этажа главной библиотеки. Метод может быть и сработает в конце концов, но на практике вам нужно знать побольше о книгах в вашей предметной области. Ситуации подобного недостаточно определенного запроса не так уж редки при работе с информацией в ГИС. Одна из наиболее трудных вещей - предвосхитить все возможные запросы пользователя. В конце концов, БД ГИС обычно содержит множество типов информации и разных тематических карт. Одной из самых интересных особенностей ГИС является то, что вы можете попытаться выполнить поиск или исследовать взаимосвязи, которые не предполагались до реализации системы. К сожалению, иерархическая структура не очень подходит для этого из-за ее жесткой ключевой структуры. Помимо этого сурового ограничения иерархическая структура часто порождает большие индексные файлы. Это требует дополнительных затрат памяти для хранения данных и иногда вносит свой вклад также и в рост времени доступа. Сетевые структуры Как мы видели, возможности быстрого поиска, выполняемого в иерархической структуре данных, определяются структурой самого дерева. Атрибутивные и геометрические данные могут храниться в разных местах, что потребует установления большого числа связей между графической и атрибутивной частями БД. В таком случае потенциальное число ветвлений и связанных с ними ключей иерархической структуры может стать очень большим. Такая неуклюжесть возникает главным образом потому, что иерархическая структура данных больше всего подходит, когда между элементами данных требуется устанавливать связи "один к одному" или "один ко многим". Сетевые БД ГИС используют отношение "многие ко многим", при котором один элемент может иметь многие атрибуты, при этом каждый атрибут связан явно со многими элементами. Например, исследуемый участок может иметь много квадратов, с каждым из которых может быть связаны несколько животных и растительных видов, при том, что каждый вид может присутствовать в более чем одном квадрате. Для реализации таких отношений вместе с каждым элементом данных может быть связана специальная переменная, называемая указателем (pointer), которая направляет нас ко всем другим элементам данных, связанным с этим (Рисунок 4.7). Вместо того, чтобы ограничиваться древовидной структурой связей, каждый отдельный элемент данных может быть прямо связан с любым местом базы данных, без введения отношения "предок-потомок". Указатели - обычное явление в языках программирования вроде Си и Си++, и некоторое знание их поможет вам в понимании того, как именно эти приемы реализуются. Для наших целей будет достаточно графической иллюстрации. Рисунок 4.7 показывает два квадрата (№3 и №7) исследовательской площадки №4. Обратите внимание на то, как указатели используются для связи отдельных квадратов с представляющими их видами. Указатели обеспечивают и обратную связь от видов к квадратам, в которых они находятся. Сетевые структуры обычно рассматриваются как усовершенствование иерархических структур, поскольку они менее жесткие и могут представлять отношение "многие ко многим". Поэтому они допускают гораздо большую гибкость поиска, нежели иерархические структуры. Также в отличие от иерархических структур они уменьшают избыточность данных. Их главным недостатком является то, что в крупных БД ГИС количество указателей может стать очень большим, требуя значительной затрат памяти. Вдобавок, хотя связи между элементами данных более гибкие, они все же должны быть явно определены с помощью указателей. Многочисленные возможные связи могут превратиться в весьма запутанную сеть, приводя часто к путанице, потерянным и ошибочным связям. Новички часто оказываются подавлены этими условиями, но опытные пользователи могут достичь высокой эффективности с такими системами и часто предпочитают их перед другими. 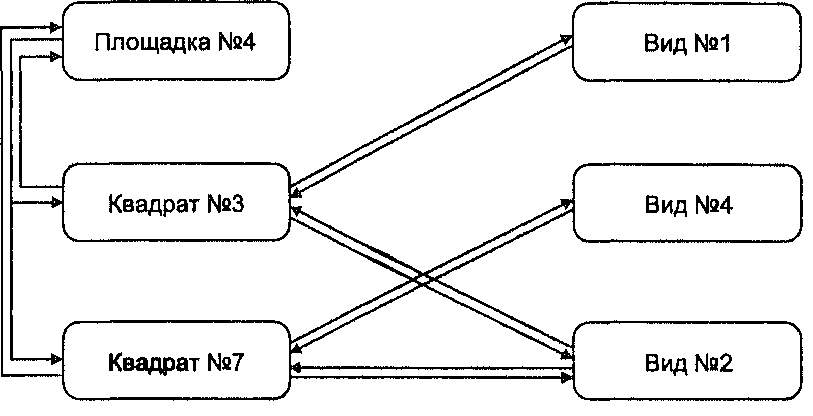 Рисунок 4.7. Сетевая структура БД. Эта структура позволяет пользователю перемещаться от одного элемента данных к другому через цепочку указателей, которые выражают взаимоотношения между элементами данных. Реляционные базы данных Недостатков большого количества указателей можно избежать используя еще одну структуру баз данных - реляционную. В ней данные хранятся как упорядоченные записи или строки значений атрибутов. Атрибуты объектов группируются в отдельных строках в виде так называемых отношений (relations), поскольку они сохраняют свои положения в каждой строке и определенно связаны друг с другом (Рисунок 4.8) [Healey, 1991]. Каждая колонка содержит значения одного атрибута для всего набора объектов. Например, может быть колонка с номерами квадратов (один атрибут). В другой колонке может быть дополнительная информация, относящаяся к сборщику данных, в третьей - дата сбора данных, в четвертой - номер площадки. Атрибуты объектов могут также объединяться в другие, связанные, таблицы. 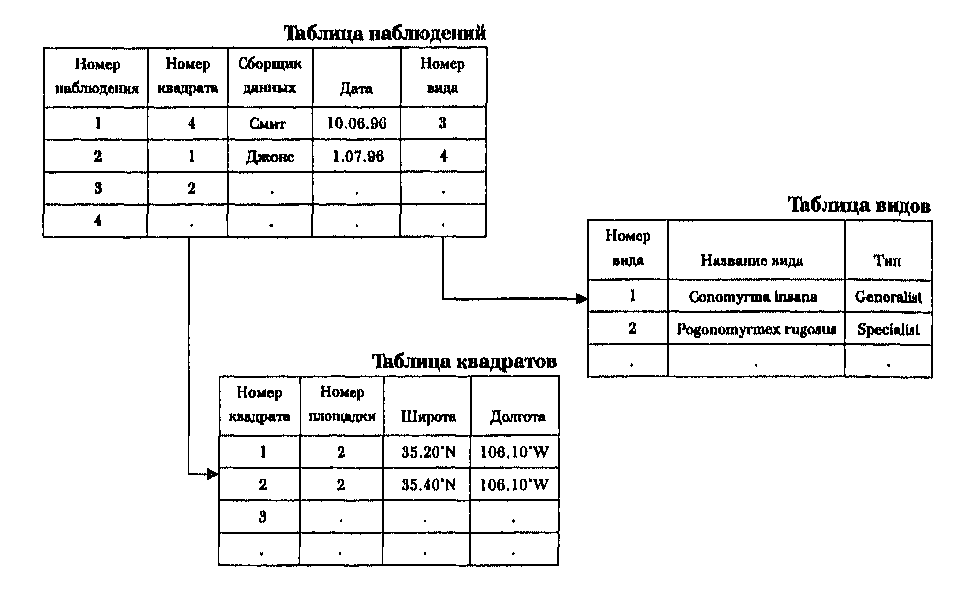 Рисунок 4.8. Реляционная структура БД. Реляционные системы основаны на наборе математических принципов, называемых реляционной алгеброй или алгеброй отношений [Ullman, 1982], устанавливающей правила проектирования и функционирования таких систем. Поскольку реляционная алгебра основывается на теории множеств, каждая таблица отношений функционирует как множество, и первое правило гласит, что таблица не может иметь строку, которая полностью совпадает с какой-либо другой строкой. Поскольку каждая из строк уникальна, одна или несколько колонок могут использоваться для определения критерия поиска. Так, примером использования одной колонки для определения критерия поиска может быть выбор уникального личного номера социального страхования, номера телефона, домашнего адреса и других, имеющихся в других колонках той же таблицы при выборе Глава 4 определенного имени из первой колонки. Такой критерий поиска называется первичным ключом (primary key) для поиска значений в других колонках базы данных [Date, 1986]. Всякая строка таблицы должна иметь уникальное значение в колонке первичного ключа, в противном случае мы не сможем однозначно идентифицировать объекты по первичному ключу. Реляционные системы ценны тем, что позволяют нам собирать данные в достаточно простые таблицы, при этом задачи организации данных также просты. При необходимости мы можем стыковать строки из одной таблицы с соответствующими строками из другой таблицы, используя связующий механизм, называемый реляционным соединением (relational join). Поскольку реляционные системы преобладают в ГИС и поскольку для ГИС созданы довольно большие базы данных, этот процесс широко распространен, и вам нужно повнимательнее его рассмотреть. Любое количество таблиц может быть "связано". Соединение происходит по равенству значений колонки первичного ключа одной таблицы с другой колонкой второй таблицы. Колонка второй таблицы, с которой связан первичный ключ, называется внешним ключом (foreign key). Опять же, значения связанных строк предполагаются находящимися в тех же позициях для гарантии соответствия. Эта связь означает, что все колонки второй таблицы привязаны к колонкам первой таблицы. Благодаря этому каждая таблица может быть наиболее простой, облегчая управление данными. Вы можете привязать сюда третью таблицу, взяв колонку второй таблицы, которая будет использоваться как первичный ключ к соответствующей ключевой колонке (теперь называемой внешним ключом) третьей таблицы. Процесс может продолжаться присоединением все новых простых таблиц для проведения довольно сложного поиска, причем набор таблиц остается очень простым и легко поддерживаемым. Этот подход устраняет путаницу, присущую разработке баз данных с использованием сетевых систем. Чтобы мы могли устанавливать реляционные соединения, каждая таблица должна иметь хотя бы одну общую колонку с другой таблицей, с которой мы желаем установить такое соединение. Эта избыточность - как раз то, что прежде всего и обеспечивает реляционное соединение. Однако, по возможности, избыточность следует уменьшать. Для определения вида, который ваши таблицы должны иметь, установлен набор правил, называемых нормальными формами (normal forms) [Codd, 1970]. Мы рассмотрим три основные нормальные формы; существуют некоторые дополнения, но это уже скорее усовершенствования, чем собственно нормальные формы [Fagin, 1979]. Первая нормальная форма утверждает, что таблица должна состоять из строк и колонок и, поскольку колонки будут использоваться в качестве ключей поиска, в каждой из них на каждой строке должно находиться только одно значение. Представьте себе, как трудно было бы искать информацию по названию, если бы колонка названия имела по несколько значений в каждой строке. Вторая нормальная форма требует, чтобы каждая колонка, не являющаяся первичным ключом, полностью зависела от первичного ключа. Это упрощает таблицы и уменьшает избыточность ограничением, что каждая строка данных может быть найдена только через ее первичный ключ. Если вы хотите найти заданную строку, используя другие отношения, то вы можете использовать реляционное соединение вместо того, чтобы дублировать колонки в разных таблицах. Третья нормальная форма, связанная со второй, требует, чтобы колонки, которые не являются первичным ключом, "зависели" от первичного ключа, в то время, как первичный ключ не зависит от какого-либо не первичного ключа. Другими словами, вы должны использовать первичный ключ для поиска значений в других колонках, но вам не нужно использовать другие колонки для поиска значений в колонке первичного ключа. Цель, опять же, - уменьшение избыточности, использование наименьшего числа колонок. Правила нормальных форм были суммированы Кентом [Kent, 1983]. Эти правила весьма полезны и должны строго выполняться. Сказав это, все же приходится признать, что всегда существуют обстоятельства, когда такое выполнение будет невозможно или существенно снизит производительность системы [Healey, 1991]. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ ОБЪЕКТОВ И ИХ АТРИБУТОВ До сих пор мы занимались структурами данных, которые имеют мало общего с графическим представлением картографических или географических объектов. Хотя все три упомянутые системы могут использоваться для управления графикой, они мало что говорят нам о том, как сама графика будет представляться в ГИС, Мы знаем, что человеческий разум способен создавать графическое представление пространства и объектов в нем. Это представление в действительности довольно сложное, как вы увидите, когда мы попытаемся перейти к компьютерной реализации графических приемов. Главная трудность состоит в том, что наше графическое восприятие включает набор подразумеваемых отношений между элементами, расположенными на бумаге. Одни линии соединяются с другими линиями, и вместе они образуют области или многоугольники. Связь линий друге другом в пространстве выражается посредством углов и расстояний. Одни линии замкнуты, другие - нет. Одни многоугольники имеют соседей, другие - изолированы. Список возможных взаимоотношений, которые могут содержаться в чертеже, практически бесконечен. Нам нужно найти способ представления каждого объекта и каждого отношения в виде набора явных правил, которые помогут компьютеру "понять", что все эти точки, линии и области представляют нечто на земле, что они находятся в определенных местах пространства и что эти места также связаны с другими объектами в пространстве. Мы можем даже захотеть объяснить компьютеру, что многоугольник имеет непосредственного соседа слева, и этот сосед может иметь с ним общие точки и линии. В общем, нам нужно создать язык пространственных отношений. Существуют два основных метода представления географического пространства. Первый метод использует квантование (quantization), или разбиение пространства на множество элементов, каждый из которых представляет малую, но вполне определенную часть земной поверхности. Этот растровый (raster) метод может использовать элементы любой подходящей геометрической формы при условии, что они могут быть соединены для образования сплошной поверхности, представляющей все пространство изучаемой области. Хотя возможны многие формы элементов растра, например, треугольная или шестиугольная, обычно проще использовать прямоугольники, а еще лучше - квадраты, которые называются ячейками (grid cells). В растровых моделях ячейки одинаковы по размеру, но это не является обязательным требованием для разбиения пространства на элементы, которое не выполняется в не очень широко используемом подходе, называемом квадродеревом. В данном разделе мы рассмотрим модели, в которых все ячейки - одинакового размера, и представляют такое же количество географического пространства, как любые другие. Растровые структуры данных не обеспечивают точной информации о местоположении, поскольку географическое пространство поделено на дискретные ячейки конечного размера. Вместо точных координат точек мы имеем отдельные ячейки растра, в которых эти точки находятся (Рисунок 4.9). Это еще одна форма изменения пространственной мерности, которая состоит в том, что мы изображаем объект, не имеющий измерений (точку), с помощью объекта (ячейки), имеющего длину и ширину. Линии, то есть одномерные объекты, изображаются как цепочки соединенных ячеек. Опять же, здесь имеет место изменение пространственной мерности от одномерных объектов к двухмерным структурам. Каждая точка линии представляется ячейкой растра, и каждая точка линии должна находиться где-то внутри одной из ячеек растра. Легко увидеть, что эта структура данных изображает линии ступенчатым образом (Рисунок 4.9). Этот ступенчатый вид также обнаруживается при изображении областей с помощью ячеек растра (Рисунок 4.9). 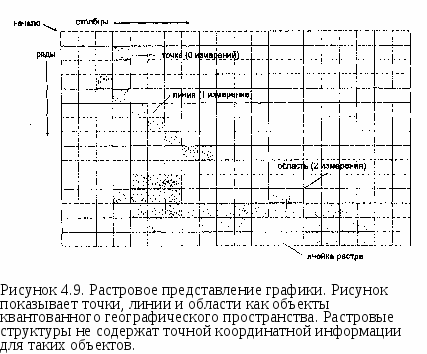 В растровых системах есть два способа включения атрибутивной информации об объектах. Простейшим является присваивание значения атрибута (например, класса растительного покрытия) каждой ячейке растра. Распределяя эти значения, мы в конечном итоге позволяем позициям значений атрибутов играть роль местоположений объектов. Например, если числом 10 мы представляем водную поверхность, и записываем его в левую верхнюю ячейку растра, то по умолчанию эта ячейка является участком земной поверхности, представляющем воду. Таким образом мы можем каждой ячейке на данной карте присвоить только одно значение атрибута. Альтернативный подход, а на самом деле, - расширение только что описанного, состоит в связывании каждой ячейки растра с базой данных, так что любое число атрибутов может быть присвоено каждой ячейке растра. Этот подход становится все более преобладающим, так как он уменьшает объем хранимых данных и может обеспечивать связь с другими структурами данных, которые также используют СУБД для хранения и поиска данных. Хотя абсолютное местоположение не является явной частью растровой структуры данных, оно подразумевается относительным положением ячеек. Таким образом, линия представляется ячейками в определенных положениях относительно друг друга; области представляются смежными ячейками. Как вы могли догадаться, чем больше размер ячейки, тем большую площадь земли она покрывает, то есть, тем ниже (грубее) разрешение (resolution) растра, и тем меньше точность положений точек, линий и областей, представленных данной структурой. Ячейки растра примыкают друг к другу для покрытия всей области. Благодаря этому мы можем использовать номера ячеек по вертиткали и горизонтали в качестве координат, а также можем сопоставить с этими номерами обычные декартовы координаты (см. Главу 3). Как мы уже видели, системы прямоугольных координат используют картографические проекции для приблизительного изображения трехмерной формы участка земли. Ячеечное представление может иметь встроенную координатную систему, которая лучше аппроксимирует абсолютное положение, чем декартовы координаты. Например, пикселы изображений дистанционного зондирования (см. Главу 3) создаются в некоторой проекции, и для измерений на растре может помещена более точная координатная сетка. Однако в общем случае точные измерения на любой растровой структуре затруднены. Поэтому когда требуются точные измерения, растровые структуры используются реже, чем другие типы. Растровые структуры данных могут показаться плохими из-за отсутствия точной информации о местоположении. На самом деле верно обратное. Растровые структуры имеют много преимуществ перед другими. В частности, они относительно легко понимаются как метод представления пространства. Возможно, некоторые из вас видели распечатки изображений героев мультфильмов на календарях, отпечатанных на АЦПУ и столь распространенных в 60-х и 70-х годах. Если нет, то вы уж наверняка знакомы с телевидением, которое использует то же растровое представление изображений. Немногие из нас имеют трудности в опознавании актеров по их изображениям на экране телевизора, даже несмотря на то, что все представлено набором точек (пикселов). В действительности, родство между пикселом, используемом в дистанционном зондировании, и ячейкой, используемой в ГИС, обеспечивает легкий перенос спутниковых изображений в ГИС, основанные на растре, не требуя каких-либо изменений. Это - еще одно преимущество растровых структур данных перед другими. Еще одной замечательной характеристикой растровых систем является то, что, как вы увидите в Главе 12, многие функции, особенно связанные с операциями с поверхностями и наложением (overlay), легко выполняются на этом типе структур данных. Среди главных недостатков растровой структуры данных - уже упоминавшаяся проблема низкой пространственной точности, которая уменьшает достоверность измерения площадей и расстояний, и необходимость большого объема памяти, обусловленная тем, что каждая ячейка растра хранится как отдельная числовая величина. Последняя проблема сегодня не так серьезна, как прежде, благодаря огромному росту емкости внешних запоминающих устройств компьютеров. Кроме того, как вы увидите позднее в этой главе, существуют методы уменьшения необходимого для хранения объема памяти, использующие упаковку групп ячеек растра в более компактные формы. Хотя объем памяти и не является теперь главным ограничением в использовании растровых структур, даже самые быстрые компьютеры могут быть загружены до состояния черепашьего хода вычислениями высокой сложности, выполняемыми на больших изображениях. Второй метод представления географического пространства, называемый векторным (vector), позволяет задавать точные пространственные координаты явным образом. Здесь подразумевается, что географическое пространство является непрерывным, а не квантованным на дискретные ячейки. Это достигается приписыванием точкам пары координат (X и Y) координатного пространства, линиям - связной последовательности пар координат их вершин, областям - замкнутой последовательности соединенных линий, начальная и конечная точки которой совпадают (Рисунок 4.10). 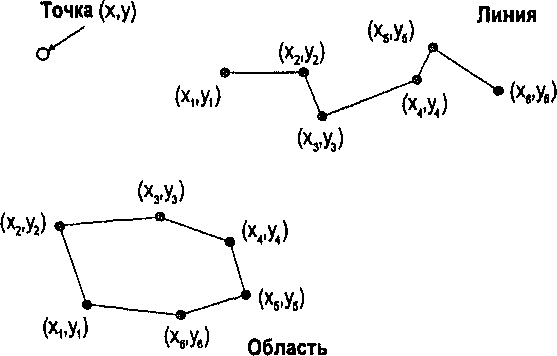 Рисунок 4.10. Векторное представление графики. Рисунок показывает точки как отдельные пары координат, линии - как группы пар координат, области - как соединенные линии с началом и концом в одной точке. Векторная структура данных показывает только геометрию картографических объектов. Чтобы придать ей полезность карты, мы связываем геометрические данные с соответствующими атрибутивными данными, хранящимися в отдельном файле или в базе данных. Благодаря этому контурное изображение объектов становится больше похожим на карту. В растровой структуре мы записывали значение атрибута в каждую ячейку, в векторном же представлении мы используем совсем другой подход, храня в явном виде собственно графические примитивы без атрибутов и полагаясь на связь с отдельной атрибутивной базой данных. В векторных структурах данных линия состоит двух или более пар координат. Для одного отрезка достаточно двух пар координат, дающих положение и ориентацию в пространстве. Более сложные линии состоят из некоторого числа отрезков, каждый из которых начинается и заканчивается парой координат. Для кривых линий может использоваться приближенное изображение с помощью большого числа коротких прямых отрезков. Чем короче отрезки, тем более точно они представляют сложную линию. Таким образом, мы видим, что хотя векторные структуры данных лучше представляют положения объектов в пространстве, они не абсолютно точны. Они все же являются приближенным изображением географического пространства. Хотя некоторые линии существуют самостоятельно и имеют определенную атрибутивную информацию, другие, более сложные наборы линий, называемые сетями, содержат также дополнительную информацию о пространственных отношениях этих линий. Например, дорожная сеть содержит не только информацию о типе дороги и ей подобную, она показывает также возможное направление движения. Эта информация должна быть присвоена каждому отрезку, чтобы сообщить пользователю, что движение может продолжаться вдоль каждого отрезка до изменения атрибутов, возможно, до того момента, когда двухсторонняя улица станет односторонней. Другие коды, связывающие эти отрезки, могут включать информацию об узлах, которые их соединяют. Узел, например, может иметь знак останова, светофор или знак запрета разворота. Все эти дополнительные атрибуты должны быть определены по всей сети, чтобы компьютер знал присущие реальности отношения, которые этой сетью моделируются. Такая явная информация о связности (connectivity) и пространственных отношениях называется топологией (topology). Мы вернемся к этой теме, когда будем рассматривать векторные модели данных, которые мы можем создать на основе базовой векторной структуры данных. *То же, что многоугольник в геометрии — прим. перев. Площадные объекты могут быть представлены в векторной структуре данных аналогично линейным. Соединяя отрезки линии в замкнутую петлю, в которой первая пара координат первого отрезка является одновременно и последней парой координат последнего отрезка, мы создаем область, или полигон (polygon)*. Как с точками и линиями, так и с полигонами связывается файл, содержащий атрибуты этих объектов. Вообще говоря, картографы предпочитают векторные структуры данных перед растровыми из-за их сходства с графическими структурами, чаще всего связываемыми с бумажными картами. За некоторыми исключениями, картографические документы, создаваемые на основе векторных структур данных, сильно напоминают нарисованные от руки карты. Только лишь вывод карт не является главной целью ГИС, но способность измерять и анализировать картографически организованные данные. А для этого необходим какой-то способ комбинирования графических объектов с их атрибутами. Мы упомянули в этой связи использование отдельных файлов с атрибутами и баз данных. Структуры данных должны разрабатываться так, чтобы обеспечивать эту связь, явно или косвенно. Кроме того, существуют многие другие характеристики графических структур, важные с точки зрения анализа карт. Мы должны перейти от простых структур данных к тому, что часто называют моделями данных, которые больше похожи на карты в смысле способности участвовать в анализе. Мы рассмотрим некоторые их типы, как для растровых, так и для векторных структур. МНОГОСЛОЙНЫЕ МОДЕЛИ ДАННЫХ ГИС В то время, как растровые и векторные структуры данных дают нам средства отображения отдельных пространственных феноменов на отдельных картах, все же существует необходимость разработки более сложных подходов, называемых моделями данных, для включения в базу данных взаимоотношений объектов, связывания объектов и их атрибутов, обеспечения совместного анализа нескольких слоев карты. Вначале мы рассмотрим растровые модели, затем - векторные. После этого мы сделаем еще один шаг и рассмотрим способы комбинирования этих моделей данных в системы, в данном случае - геоинформационные системы. Растровые модели Как говорилось в начале нашего обсуждения растровых структур данных, каждая ячейка в простейшей такой структуре связана с одним значением атрибута. Для создания растровой тематической карты мы собираем данные об определенной теме в форме двухмерного массива ячеек, где каждая ячейка представляет атрибут отдельной темы. Такой двухмерный массив называется покрытием (coverage). Мы можем использовать покрытия для представления различных типов тематических данных (землепользование, растительность, тип почвы, поверхностная геология, гидрология и т.д.). Кроме того, этот подход позволяет нам фокусировать внимание на объектах, распределениях и взаимосвязях тем без ненужной путаницы. Поскольку чаще всего мы интересуемся взаимосвязями одной темы, скажем, типа почвы, с другими, то создаем отдельное покрытие для каждой дополнительной темы. Тогда мы можем сложить эти покрытия наподобие слоеного пирога, в которой сочетание всех тем может адекватно моделировать все необходимые характеристики области изучения. Если мы интересуемся только природными феноменами, то каждый важный компонент физической географии будет представлен отдельно, а вместе они дадут нам полный, многоаспектный вид изучаемой области. Существует несколько способов хранения и адресации значений отдельных ячеек растра, их атрибутов, названий покрытий и легенд. Среди первых попыток можно упомянуть подход под названием GRID/LUNR/ MAGI [Burrough, 1983] (Рисунок 4.11а); все ранние растровые ГИС использовали именно его. В этой модели каждая ячейка содержит все атрибуты вроде вертикального столбика значений, где каждое значение относится к отдельной теме. Так, значение атрибута типа почвы в позиции Х=10, Y= 10 будет находиться рядом со значением атрибута типа растительности в той же позиции Х= 10, Y= 10. Вы могли бы представить это себе как геологический керн, в котором каждый тип породы лежит поверх следующего, и для того, чтобы получить картину всей области исследования, нужно сложить вместе данные многих кернов. Преимуществом, конечно, является то, что относительно легко выполняется вычислительное сравнение многих тем или покрытий для каждой ячейки растра. Но в то же время, неудобно сравнивать группы ячеек одного покрытия с группами ячеек другого покрытия, поскольку каждая ячейка должна адресоваться индивидуально. Подумайте хорошенько о том, что бы вы хотели изменить в этом подходе. Возможно, вы подумали о шахматной доске с ее черными и белыми квадратами. Если каждый из таких квадратов представляет тип ландшафта (например, черный - суша, белый - водная поверхность), то мы создали простое покрытие. Но как атрибуты нашего ландшафтного покрытия соединены физически? Мы можем взять в руки всю доску, поскольку она -физически связная структура. Аналогичным образом, тематическая карта представляет все разнообразные значения темы как единый связный объект. Вполне естественно сходство между доской как единого целого для игры и карты как единого целого для хранения пространственной информации. В действительности, с небольшим изменением аналогии с шахматной доской, мы можем рассмотреть вторую модель растровых данных, которую назовем моделью данных IMGRID (Рисунок 4.11b) потому, что она использовалась в ранней ГИС с таким названием [Burrough, 1983]. Здесь мы примем, что белые ячейки это "вода", а черные - "не вода". Мы упростили тему нашей шахматной карты до хранения одного простого атрибута, а не целой темы. В этом случае нам нет необходимости хранить широкий спектр значений для каждого покрытия. Вместо этого мы можем использовать числа 1 (белые квадраты) для обозначения присутствия воды и 0 (черные квадраты) - для обозначения ее отсутствия. А как бы мы представили тематическую карту землепользования, содержащую, скажем, четыре категории - зоны отдыха, сельского хозяйства, промышленности и жилья? Каждый из этих атрибутов должен быть выделен как самостоятельный слой. Один слой содержал бы признак только сельского хозяйства, 1 и 0 для него означали бы соответственно наличие и отсутствие такой деятельности в каждой ячейке растра. Аналогично представляются отдых, промышленность и жилье, причем прямо адресуется теперь каждый признак, а не ячейки растра, как было в модели данных GRID/LUNR/MAGI. В конечном итоге, слои можно сложить "вертикально" для получения единой карты. Система IMGRID имеет два основных преимущества. Во-первых, мы имеем непрерывную структуру, которая больше напоминает карту. То есть, мы храним двухмерные массивы чисел для разных слоев, а не массив столбиков. Во-вторых, мы уменьшили диапазон значений для каждого слоя до одного двоичного разряда. Это упростит наши вычисления и устранит необходимость в сложной легенде карты. На самом деле, поскольку каждый признак однозначно идентифицирован одним битом, мы можем не ограничиваться одним атрибутом для каждой ячейки растра, и это третье преимущество. Например, в некоторой ячейке растра мы можем иметь частично зоны сельского хозяйства и отдыха. Поскольку каждый из этих атрибутов землепользования хранится в отдельном слое, мы можем показать, что оба вида землепользования имеют место в пределах пространства этой ячейки растра. Конечно, мы можем встретить трудности, создавая объединенное тематическое покрытие, если внутри некоторых ячеек присутствуют несколько признаков. Чтобы избежать этой проблемы, нам нужно обеспечить, чтобы каждая ячейка имела одно значение для каждого показателя. Модель IMGRID выглядит более понятной с точки зрения картографического представления. Более того, она дает преимущество для компьютера в использовании слоя как прямо адресуемого объекта. Ее ограничения происходят в основном из-за проблемы взрывного роста количества элементов данных. Представьте на минуту, что вы имеете базу данных из 50-ти тем (что вполне возможно). Допустим, что в среднем имеется 10 категорий в каждой теме. Каждая тема должна быть разделена на бинарные (из нулей и единиц) слои, по одному на каждую категорию. Итого, для представления этой вполне умеренной базы данных вам потребуется 10 х 50 = 500 слоев. Хотя программное обеспечение и позволяет управлять таким большим "хозяйством", нам нужен более эффективный способ представления нашей базы данных, такой, который не создает так много 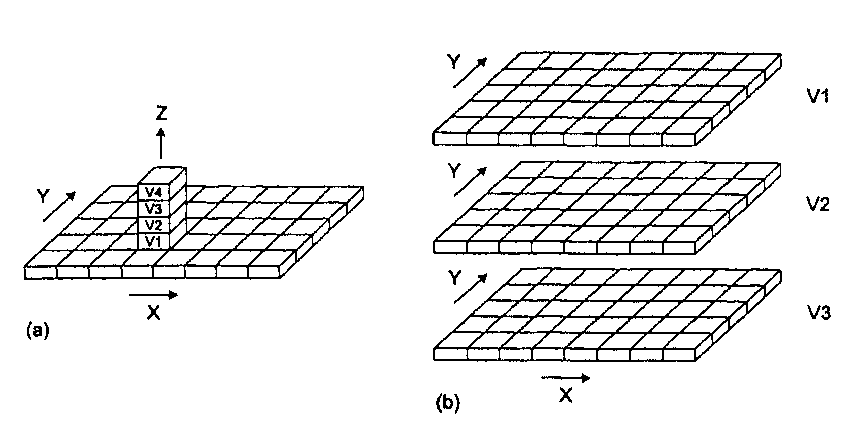 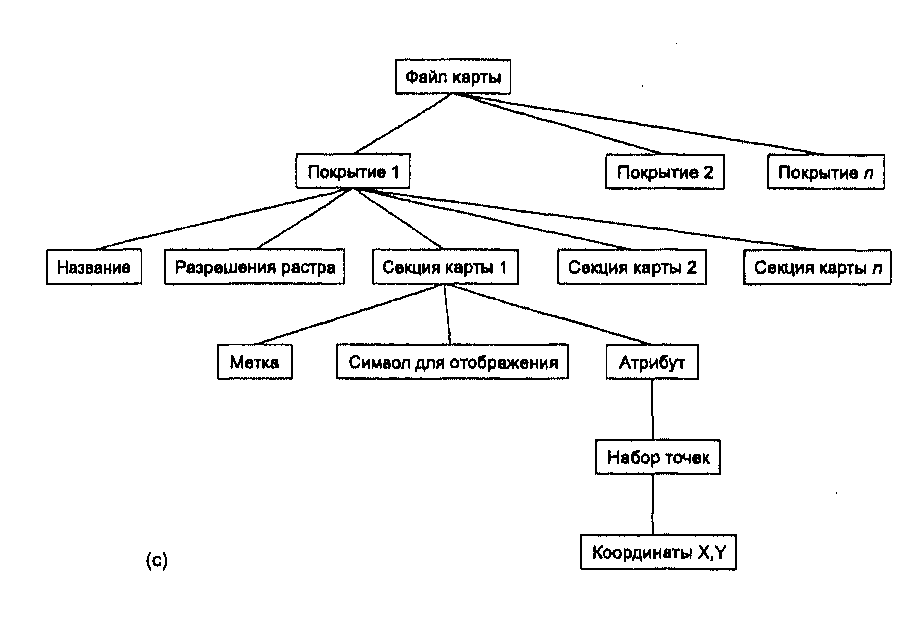 Рисунок 4.11. Три растровые модели данных для множественных покрытий: а) Модель GRID/LUNR/MAGI; b) Модель IMGRID; с) Модель MAP. Картографические и геоинформационные структуры данных элементов данных, которыми нужно управлять. Рассматривая далее этот подход, представьте себе, как много значений придется модифицировать и записывать для создания каждой новой темы. Наша третья растровая модель, которую мы назовем MAP по названию системы Пакета анализа карт (Map Analysis Package, MAP) [Burrough, 1983], разработанной Д. Томлин для своей докторской диссертации, формально объединяет преимущества двух предыдущих моделей. В этой модели данных (Рисунок 4.11с) каждое тематическое покрытие записывается и выбирается отдельно по имени карты или названию, что достигается записью каждого показателя (картографической секции) темы покрытия как отдельного числового кода или метки, которая может быть доступна отдельно при выборке покрытия. Метка соответствует части легенды, и с ней связан собственный приписанный ей символ. Таким образом, легко выполняются операции над отдельными ячейками растра и группами похожих ячеек, а результат изменений величины требует перезаписи только одного числа на картографическую секцию, упрощая тем самым вычисления. Главное преимущество метода MAP состоит в том, что он обеспечивает легкую манипуляцию значениями атрибутов и наборами ячеек растра в отношении "многие к одному". Модель данных MAP - одна из наиболее используемых растровых моделей на рынке ГИС. Ее можно найти во многих формах, от ее изначальной версии на больших машинах до вариантов для Macintosh и PC и современных рабочих станций под управлением UNIX. Гибкость и легкость использования сделали ее легкодоступным средством для обучения геоинформатике, она может использоваться в дополнительных модулях коммерческих ГИС-пакетов и даже как основа для полнофункциональных растровых ГИС. В то время как растровые ГИС традиционно разрабатывались для представления одиночных атрибутов, хранимых индивидуально для каждой ячейки растра, некоторые из них достигли состояния использования прямых связей с существующими СУБД. Такие расширения растровой модели данных позволили также установить прямую связь с ГИС, использующими векторную структуру графических данных. Поскольку такие интегрированные растрово-векторные системы включают модули, которые преобразуют информацию из растровой формы в векторную и обратно, пользователь может использовать достоинства обеих структур данных. Процесс преобразования часто прозрачен, так что пользователю даже не нужно беспокоиться об исходной структуре данных. Эта возможность особенно важна, поскольку она усиливает взаимодействие между программным обеспечением традиционной обработки цифровых изображений и геоинформационными системами. Сегодня уже многие программные системы имеют оба набора функций, и еще больше таких систем появится в будущем. Благодаря еще и взаимодействию с существующими статистическими пакетами мы быстро приближаемся к системам, которые работают с множеством пространственных и непространственных аналитических, методов, а в результате - к периоду расцвета компьютерной географии. Методы сжатия растровых данных Перед тем как закончить обсуждение растровых моделей данных, мы должны рассмотреть четыре метода хранения растровых данных, которым свойственна существенная экономия дискового пространства. Методы сжатия растровых данных работают внутри подсистемы хранения и редактирования ГИС, но они могут вызываться и напрямую на этапе ввода информации в ГИС. Мы вернемся к этим методам в следующей главе при рассмотрении ввода данных. Подходы, освещаемые в этой главе, проиллюстрированы на Рисунке 4.12. Первый метод сжатия растровых (и не только растровых) данных называется групповым кодированием. Когда-то растровые данные вводились в ГИС с помощью пронумерованной прозрачной сетки, которая накладывалась на кодируемую карту. Каждая ячейка имела численное значение, соответствующее данным карты, которые вводились (обычно с клавиатуры) в компьютер. Например, для карты размером 200 х 200 ячеек потребуется ввести 40'000 чисел. Если ваш преподаватель сейчас услышит ваше хихиканье, не удивляйтесь, обнаружив себя за этим занятием в качестве упражнения по истории ГИС или урока скромности. На самом деле, вы можете попробовать его как-нибудь, если у вас есть доступ к какой-либо растровой ГИС. Начав вводить, вы быстро обнаружите повторения данных, которые могут быть использованы для уменьшения работы. Конкретнее, в каждом ряду существуют длинные цепочки одинаковых чисел. Подумайте, сколько времени вы сэкономите на одной строке, если бы могли сказать компьютеру, что, например, с позиции 8 по позицию 56 идут одни единицы, а с 57-й позиции до конца ряда идут двойки. В действительности, вы могли бы также сохранить немало объема памяти, записывая только начальную и конечную позицию для каждой цепочки и значение, которое в ней присутствует. В этом и состоит идея группового кодирования. Конечно, этот метод действует в пределах одной строки растра. Что, если бы вы могли сказать компьютеру начать с отдельной ячейки со значением 1, затем перейти в определенном направлении, скажем вертикально, на 27 ячеек и тогда изменить значение. Это позволило бы кодировать цепочки в любом направлении. Но принцип может быть расширен и дальше. Допустим,  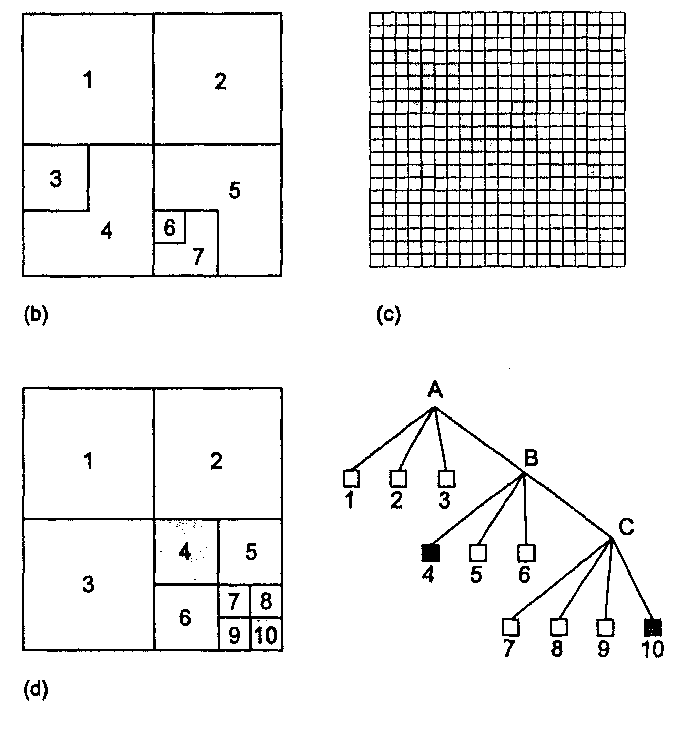 Рисунок 4.12. Методы сжатия растровых данных, а) групповое кодирование, b) блочное кодирование, с) цепочечное кодирование, d) квадродерево. |
