Инструкция к лабораторным работам
 Скачать 5.94 Mb.
|
КОНТРОЛЬНЫЕ ВОПРОСЫ И ЗАДАНИЯЧто такое магнитное поле? Источники магнитного поля? В чем состоит физический смысл магнитной индукции? Единица ее измерения. Записать закон Био-Савара-Лапласа, дать пояснения. Изобразить магнитное поле кругового тока. Является ли оно однородным? Сформулировать принцип суперпозиции магнитных полей. ТЕСТОВЫЕ ЗАДАНИЯ
Установка представляет собой пластмассовое кольцо с намотанной на него проволокой (рис. 3). Кольцо располагается в вертикальной плоскости. В центре кольца на вертикальной оси (игле) вращается магнитная стрелка МС. Величина силы тока в проволоке регулируется с помощью реостата R, а контролируется миллиамперметром. Направление тока можно изменить на противоположное переключателем П. Если через кольцевой контур, установленный в плоскости магнитного меридиана, пропускать электрический ток, то на магнитное поле Земли  наложится перпендикулярное ему поле  , создаваемое этим током. Магнитная стрелка при этом установится по направлению результирующего вектора магнитной индукции Земли и кругового тока  (рис. 2). Из геометрии (рис. 2) следует, что  , (6)где - угол поворота стрелки после включения тока в контуре. 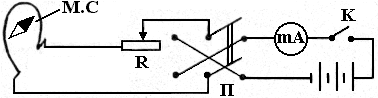 Рис. 3. Электрическая схема установки. Установка представляет собой пластмассовое кольцо с намотанной на него проволокой (рис. 3). Кольцо располагается в вертикальной плоскости. В центре кольца на вертикальной оси (игле) вращается магнитная стрелка МС. Величина силы тока в проволоке регулируется с помощью реостата R, а контролируется миллиамперметром. Направление тока можно изменить на противоположное переключателем П. ОТЧЕТ
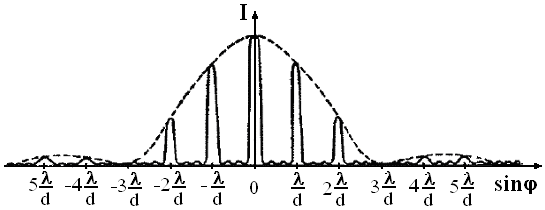
ЛАБОРАТОРНАЯ РАБОТА № 10 ИЗУЧЕНИЕ ДИФРАКЦИИ ФРАУНГОФЕРА С ПОМОЩЬЮ ЛАЗЕРА Цель работы: изучить явление дифракции света; определить длину волны лазерного излучения при дифракции от различных препятствий; определить радиус монодисперсных частиц и период дифракционной решетки.  Рис. 1. Принцип Гюйгенса. Теоретическое введение. Под дифракцией света понимают огибание световыми волнами препятствий, проникновение света в область геометрической тени. Дифракция наблюдается при условии, что размеры препятствия сравнимы с длиной волны света. Качественно проникновение световых волн в область геометрической тени может быть объяснено с помощью принципа Гюйгенса, согласно которому, каждая точка пространства, до которой доходит волна в момент времени t, является центром вторичных волн; огибающая этих волн дает положение фронта волны в следующий момент времени t+∆t (рис. 1).  Рис. 2. Проникновение световой волны в область геометрической тени. Пусть на непрозрачную плоскую преграду с отверстием падает перпендикулярно ей свет с плоским волновым фронтом (рис. 2). Согласно принципу Гюйгенса, каждая точка отверстия служит центром вторичных волн, которые в однородной и изотропной среде будут сферическими. Построив огибающую вторичных волн (пунктирная линия на рис. 2), можно убедиться в том, что за отверстием волна проникает в область геометрической тени, огибая края преграды. Таким образом, принцип Гюйгенса позволяет качественно проанализировать распространение света в среде или вакууме, геометрически построить волновую поверхность и решить задачу о направлении распространения волнового фронта. Однако этот принцип не затрагивает вопроса об амплитуде и интенсивности волн, распространяющихся по различным направлениям. Французский ученый Френель дополнил принцип Гюйгенса идеей об интерференции вторичных волн. Учет амплитуд и фаз вторичных волн позволяет найти амплитуду результирующей волны в любой точке пространства. Согласно принципу Гюйгенса-Френеля, каждый элемент dS волновой поверхности S (рис. 3) служит источником вторичной сферической волны, амплитуда которой пропорциональна величине площади элемента dSи убывает с расстоянием r от источника по закону 1/r. Поэтому уравнение вторичной волны, приходящей в точку Р от некоторого участка dS, будет выглядеть следующим образом:  , (1) Рис. 3. Элемент волновой поверхности. где  - фаза колебания в месте расположения элемента волновой поверхности dS,  - волновое число, - длина световой волны, r- расстояние от элемента поверхности dS до точки Р; a0 - множитель, определяемый амплитудой светового колебания в том месте, где находится элемент поверхности dS; K() - коэффициент, зависящий от угла φ между нормалью n к площадке dS и вектором r (При φ = 0 этот коэффициент максимален, при φ=π/2он обращается в нуль), dE - напряженность электрического поля световой волны в точке Р. Результирующее колебание в точке Р представляет собой суперпозицию колебаний от всех источников dS, взятых по всей волновой поверхности S: . (2)Эта формула является аналитическим выражением принципа Гюйгенса-Френеля: результирующее колебание в любой точке пространства представляет собой результат суперпозиции когерентных вторичных волн, излучаемых фиктивными источниками, которыми служат бесконечно малые элементы волновой поверхности S, причем сложение колебаний производится с учетом амплитуд и фаз вторичных волн. Зная амплитуду результирующей волны Ео , нетрудно определить распределение интенсивности Iв любой точке пространства, в том числе и на экране, так как  . (3)где εo - электрическая постоянная, ε - диэлектрическая проницаемость среды, μo - магнитная постоянная, μ - магнитная проницаемость среды. Решение уравнения (2) совместно с (3) позволяет рассчитать интенсивность света, дифрагированного на любых препятствиях. На практике обычно различают два вида дифракции. Если источник света и точка наблюдения Р расположены от препятствия настолько далеко, что лучи, падающие на препятствие, и лучи, идущие в точку Р, образуют практически параллельные пучки, то говорят о дифракции Фраунгофера (или дифракции плоских волн). Если дифракционная картина наблюдается на конечном расстоянии от препятствия, то говорят о дифракции Френеля (или дифракции сферических волн). В данной работе изучается дифракция Фраунгофера на наиболее простых препятствиях. 1. Дифракция света на щели и на нити. 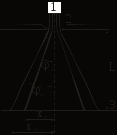 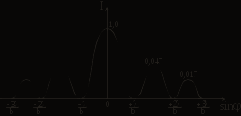 (а) (б) Рис. 4. Дифракция света на щели. Рассмотрим дифракцию Фраунгофера на бесконечно длинной щели. Для этого практически достаточно, чтобы длина щели была значительно больше ее ширины. Пусть плоская монохроматическая световая волна длиной λот источника света 1 падает нормально к плоскости расположения узкой щели 2 шириной b (рис. 4а). В соответствии с принципом Гюйгенса-Френеля, каждая точка плоскости щели 2, до которой дошел свет, становится источником вторичных волн, распространяющихся во все стороны под углами дифракции φ. Дифрагированные пучки света являются когерентными и при их наложении происходит интерференция. Интерференционная картина в виде чередования светлых (максимумы интенсивности) и темных (минимумы интенсивности) полос будет наблюдаться на экране 3, находящемся на расстоянии L от щели. Для получения четкой дифракционной картины должно выполняться условие  .Решение задачи дифракции заключается в нахождении интенсивности света в различных точках экрана. Воспользуемся результатом расчета интенсивности дифрагированного света 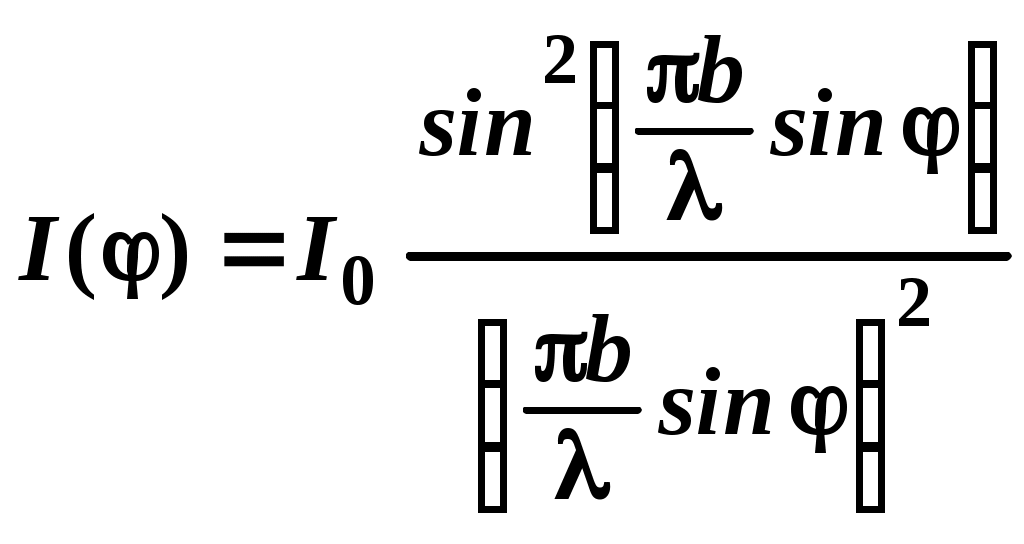 в направлении произвольного угла φ, полученным при решении уравнений (2), (3): , (4)где I0 - интенсивность света, распространяющегося под углом φ=0, т.е. в направлении падающего на щель пучка. Из выражения (4) видно, что при значении угла дифракции φ, удовлетворяющего условию  , (5)где m= ±1,±2,±3,... интенсивность равна нулю, т.к. числитель равен нулю. Величина mназывается порядком дифракции. Из условия минимумов (5) видно, что угол дифракции φ в зависимости от порядка дифракции mпринимает конкретные значения φm, поэтому в формуле (5) вместо φ будем писать φm. Окончательно условие дифракционных минимумов имеет вид:  . (6)Распределение интенсивности света на экране в зависимости от угла дифракции (дифракционный спектр) приведено на рисунке 4б. Расчеты показывают, что интенсивности центрального и последующих максимумов относятся как 1:0,047:0,017:0,0083:..., т.е. основная часть световой энергии сосредоточена в центральном максимуме. Расстояние между двумя соседними дифракционными максимумами или минимумами называется шириной дифракционной полосы ∆х. Из рисунка 4а видно, что ширина дифракционной полосы равна:  . (7)Дифракционная картина от нити будет иметь практически такой же вид, как и дифракционная картина от щели такой же толщины. Поэтому выражение (6) применимо и для расчета дифракционной картины на нити. 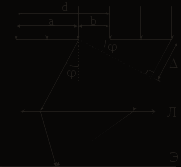 Рис. 5. Дифракционная решетка. 2. Дифракция на дифракционной решетке. Дифракционная решетка представляет собой систему параллельных щелей, расположенных на равных расстояниях друг от друга и разделенных непрозрачными участками (рис. 5). Основными параметрами дифракционной решетки является ее период d=а+b, где b - ширина щели, а - ширина непрозрачного участка между щелями, и число щелей N. В направлении угла φ каждая из щелей посылает волну с одинаковой амплитудой. Оптическая разность хода между двумя волнами, исходящими от соседних щелей (как видно из рис. 5), равна:  . (8)Если  ..., то разность фаз между всеми волнами, распространяющимися в направлении φ, окажется кратной 2π. Все световые волны в этом направлении, пересекаясь в бесконечно удаленной точке, будут взаимно усиливать друг друга. Таким образом, если мы наблюдаем дифракцию в направлении угла φ, удовлетворяющему условию  (9)то увидим дифракционный максимум, амплитуда которого будет равна сумме амплитуд всех волн, исходящих из всех щелей под углом φ. Расчет для интенсивности главных дифракционных максимумов дифракционной решетки дает следующее выражение: 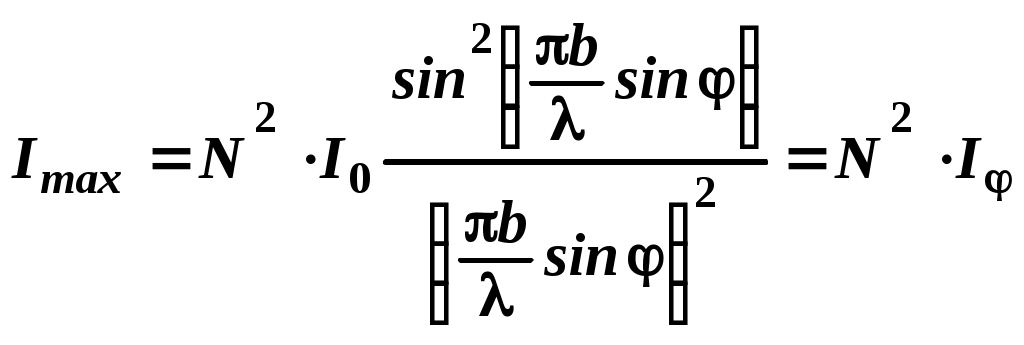 , (10)где Iφ – интенсивность от одной щели в направлении φ, I0 - интенсивность в середине дифракционной картины (напротив центра линзы). Таким образом, интенсивность главных максимумов Imax в направлении φ в N2 раз больше интенсивностиIφ, создаваемой одной щелью в этом же направлении. В результате интерференции многих пучков света в дифракционной картине появятся дополнительные, по отношению к дифракции на одной щели, минимумы, которые сделают главные максимумы уже и резче. При этом появятся также дополнительные максимумы, рассматривать которые мы не будем, т.к. интенсивность их много меньше интенсивности главных максимумов. Следовательно, главные дифракционные максимумы получаются очень узкими, положение их по этой причине может быть определено с высокой точностью, и по формуле (9) рассчитана длина волны. На рисунке 6а представлена дифракционная картина от четырех щелей (N=4). Пунктирная кривая изображает интенсивность от одной щели, умноженную на N2. Положение главных максимумов зависит от длины волны, поэтому при пропускании белого света все максимумы, кроме центрального (m=0), разложатся в спектр. Фиолетовая область спектра будет обращена к центру дифракционной картины, красная – наружу (рис. 6б). Поэтому дифракционная решетка может быть использована как спектральный прибор для разложения света в спектр и измерения длин волн. Максимум наибольшего порядка, даваемый дифракционной решеткой, определяется формулой:  (поскольку  ) . (11)Общее число главных максимумов определяется формулой:  . (12)
ОПИСАНИЕ УСТАНОВКИ
ПОРЯДОК ВЫПОЛНЕНИЯ РАБОТЫ И ЗАДАНИЯ ПРЯМОЕ ПОПАДАНИЕ ЛУЧА ЛАЗЕРА В ГЛАЗ ОПАСНО ДЛЯ ЗРЕНИЯ ! ЗАДАНИЕ I. Определение длины световой волны при дифракции на щели. Вращением поворотного барабана установить на пути лазерного пучка узкую щель и добиться четкого изображения дифракционной картины на экране. Полученное изображение перенести на лист бумаги, отметив на листе середины темных полос. Определить угловые положения середин всех видимых на экране темных полос. Для этого измеряют расстояние xm от центра дифракционной картины до середины m-ой темной полосы. Расстояние xm определяется как половина расстояния от середины левой m-ной полосы до середины соответствующей m-ной правой полосы. Индекс m указывает на номер дифракционного минимума (темной полосы) и отсчитывается от центра дифракционной картины. Далее измеряют расстояние L от щели до экрана. Тогда угловые положения темных полос φm можно определить по формуле: sinφm≈tg φm= xm /L (при этом учитывается приближенное равенство для малых углов). По формуле  вычислить длину волны λ (ширина щели b=0,1 мм). Определить среднее значение длины волны. Рассчитать относительную погрешность по формуле:  , где x – абсолютная погрешность в определении расстояния от центра дифракционной картины до середины m-ой темной полосы, L– абсолютная погрешность в определении расстояния от щели до экрана. Абсолютная погрешность измерений рассчитывается по формуле:  .Таблица 1
ЗАДАНИЕII.Определение периода дифракционной решетки. Вращением поворотного барабана поместить дифракционную решетку на пути лазерного пучка. При этом на экране появится изображение в виде далеко отстоящих друг от друга красных пятен. Определить угловое положение середин максимумов (красных пятен). Для этого определяют расстояние xm от центра дифракционной картины до соответствующего максимума. По формуле  найти период дифракционной решетки. При расчетах использовать среднее значение длины волны λ, полученное в измерениях по заданию I. Результаты измерений и вычислений занести в таблицу 2. Рассчитать погрешности измерений периода решетки Δd по формулам  ,  . Таблица 2
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
(а)
(б)