Инструкция к лабораторным работам
 Скачать 5.94 Mb.
|
|
ИНСТРУКЦИЯ к лабораторным работам Изучить введение (обработка результатов измерений). Ознакомиться с теоретическими основами лабораторной работы. Согласно списку группы, выбрать свой вариант данных. Выполнить лабораторную работу: провести расчеты, построить графики (если требуется), ответить на контрольные вопросы. Если работы выполнялись письменно, то отсканировать (сфотографировать) страницы, вставить в документ Word (можно pdf). Файл должен быть один со всеми лабораторными работами. Первый лист – титульный лист (стр.11). Прикрепить этот файл в электронный курс. Платформа ILIAS плохо работает с именами файлов набранными русскими буквами, поэтому нужно при загрузке давать имена файлам латиницей. Например, имя файла: 4TOP(s)-Ivanov-lab.doc или 4TOP(s)-Ivanov-lab.pdf (4TOP(s) – обозначение группы) ВВЕДЕНИЕ ОБРАБОТКА РЕЗУЛЬТАТОВ ИЗМЕРЕНИЙ Основная задача физического эксперимента – измерение физических величин X для дальнейшего их анализа и установления взаимосвязей между ними – физических законов. Измерение X – это процесс определения значения физической величины с помощью технических средств измерений (измерительных устройств). Результаты измерения физических величин всегда являются не абсолютно точными, а приближенными. Точность измерения зависит от чувствительности приборов и восприимчивости органов чувств экспериментатора. Абсолютной погрешностью измерения Х называют модуль разности между измеренным значением Х и ее истинным значением Хист Х = │Х – Хист│. Истинное значение Хист, вообще говоря, неизвестно. За истинное значение величины Х принимают ее среднее значение Хср. Для этого проводят несколько измерений Х1, Х2, ..., Хn и рассчитывают Хср как 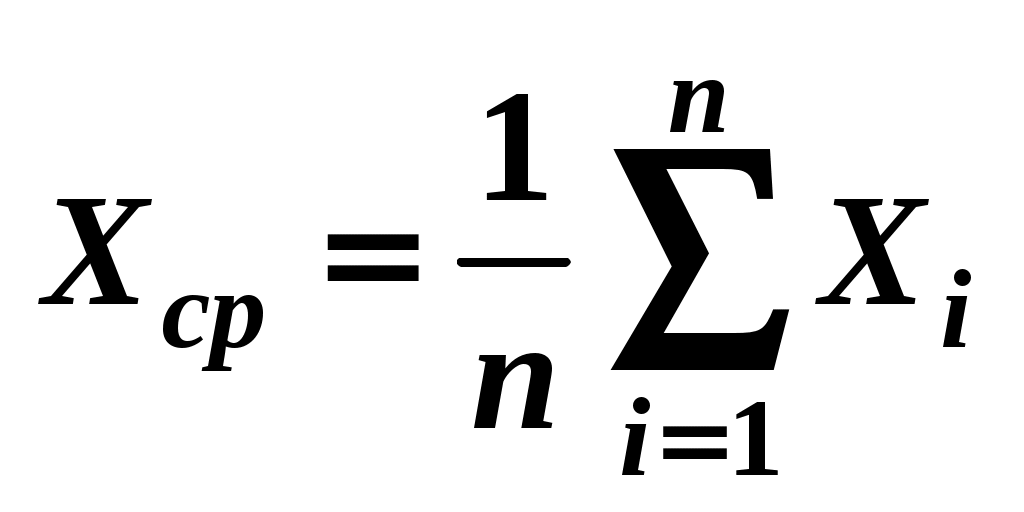 ,где n число измерений. Чем больше проведено измерений Хi, тем больше вероятность того, что ошибки разных знаков компенсируют друг друга, и тем ближе будет Хср к истинному значению Хист. Абсолютная погрешность измерения определяет количественное отклонение измеряемой величины от истинного значения. Однако она не всегда оказывается наглядной. Допустим, что X=5 см. Много это или мало? Если измеряется длина Х подошвы обуви, то это много. Если Х длина комнаты, то это мало. Если же Х расстояние между автобусными остановками, то это ничтожно мало. Критерием качества проводимых измерений является отношение абсолютной погрешности измеряемой величины X к её среднему значению Xср, так называемая относительная погрешность 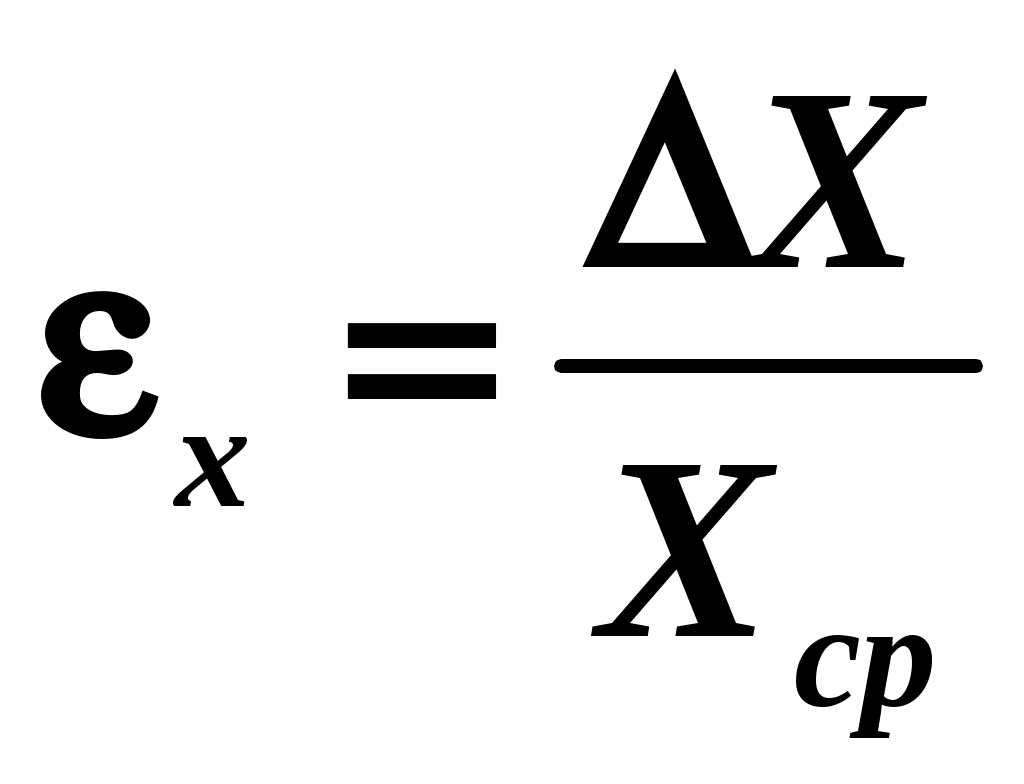 ,которую можно выразить в процентах, умножив на 100%. Относительная ошибка, указанная в процентах, округляется до целого числа. Измерения любых величин делятся на два вида: прямые и косвенные. При прямых измерениях искомая физическая величина X считывается непосредственно со шкалы прибора, предназначенного для измерения. Так, массу тела можно измерить с помощью весов, длину – с помощью линейки и т. д. При косвенных измерениях искомая величина Y не измеряется, а вычисляется по формуле с использованием величин прямых измерений Xi, входящих в расчетную формулу. Например, определение скорости тела по пройденному пути, измеренному линейкой, и времени, определенному по часам; или определение плотности тела по массе, измеренной на весах, и объему тела, определенному с помощью мензурки с водой. Остановимся подробнее на методах расчета погрешностей (ошибок) при проведении прямых и косвенных измерений. ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТИ ПРЯМЫХ ИЗМЕРЕНИЙ Различают две основных группы погрешностей: систематические и случайные. В этой классификации не учитываются грубые ошибки (промахи), вызванные невнимательностью при снятии показаний со шкалы измерительных приборов, неправильной записью этих данных, а также просто неумением экспериментатора. Такие ошибки не подчиняются никакому закону. Систематические погрешности – появляются систематически при повторных измерениях одним и тем же прибором. Возникают они чаще всего ввиду неточности измерительных приборов или самого метода измерений и остаются постоянными при повторных измерениях одной и той же величины. Например, длина линейки в действительности может отличаться от того значения, которое написано на ней. Тем не менее, прибор считается исправным, если его показания отличаются от истинного значения не более чем на величину абсолютной систематической погрешности. Абсолютная систематическая погрешность имеет размерность измеряемой величины. Абсолютную систематическую погрешность прибора (инструментальную погрешность) можно определить тремя способами: а) по классу точности прибора; б) по прибору, как число с наименованием единиц измерений; в) по цене наименьшего деления шкалы прибора. а) Определение абсолютной систематической ошибки ΔХсист по классу точности прибора. Этот способ применяется, если класс точности прибора известен заранее. Например, для электроизмерительных приборов: вольтметра и амперметра. Класс точности Ex прибора указан на шкале прибора (обычно нижний левый угол) как число в десятичном формате. Систематическая ошибка определяется по формуле:  ,где  – предельное значение шкалы прибора.Например, класс точности амперметра равен 1,5, а наибольший ток, который можно измерить этим амперметром при конкретном режиме настройки, составляет 5А. Тогда систематическая погрешность  .б) Определение абсолютной систематической ошибки ΔХсист как числа с наименованием единиц измерений. Применяется для точных измерительных приборов, имеющих шкалу нониуса или микрометрическую шкалу (штангенциркуль, микрометр). В этом случае цена деления шкалы нониуса (микрометрической шкалы) указывается непосредственно на корпусе прибора как число с наименованием единиц измерения (в некоторых случаях указывается безразмерная величина в десятичном формате). Абсолютная систематическая погрешность такого измерительного прибора равна наименьшему делению шкалы нониуса (микрометрической шкалы). Например, цена деления шкалы нониуса штангенциркуля 0,1 мм, абсолютная систематическая погрешность штангенциркуля равна 0,1 мм. в) Определение абсолютной систематической ошибки ΔХсист по цене наименьшего деления шкалы прибора. Для приборов, показания которых изменяются плавно, и нет возможности определить их погрешность указанными выше методами, систематическая погрешность может быть оценена как половина минимального деления измерительной шкалы. Например, для миллиметровой измерительной линейки систематическая погрешность Δlсист= 0,5 мм. Исключения составляют измерения кварцевыми часами (стрелки передвигаются дискретно), приборами с неравномерными шкалами и электронными приборами. В этом случае систематическая погрешность принимается равной минимальному делению шкалы. Случайные погрешности – изменяются при повторных измерениях случайным образом. Случайные факторы, обуславливающие разброс измеряемой величины X, могут быть вызваны различными причинами. С одной стороны, это могут быть причины, не зависящие от измеряемой величины, например, состояние организма человека, наблюдающего за прибором, вибрация, действие внешних электромагнитных полей, высокая влажность воздуха, отклонение температуры и давления от нормальных условий. С другой – сама измеряемая величина может носить случайный характер. Ошибки такого типа подчиняются законам теории вероятности, установленным для случайных величин. Абсолютная случайная погрешность определяется всегда одинаково:  ,где  – коэффициент Стьюдента,  – стандартный доверительный интервал (среднеквадратичное отклонение результата измерения).Коэффициент Стьюдента зависит от доверительной вероятности (надежности) и количества опытов n. Надежность () – это вероятность того, что значение измеренной величины окажется в интервале от ХХ до ХХ. При построении техники всегда задается определенная надежность изделия. Каждая деталь должна соответствовать надежности не ниже той, которая предъявляется ко всему изделию в целом. Если техника сложная, то отклонение параметров деталей от заданных значений должно быть очень малым. При лабораторных измерениях обычно полагают =0,95 и ограничиваются 3–5 измерениями. Коэффициент Стьюдента tn,α можно определить по специальной таблице.Таблица. Значения коэффициентов Стьюдента
Стандартный доверительный интервал 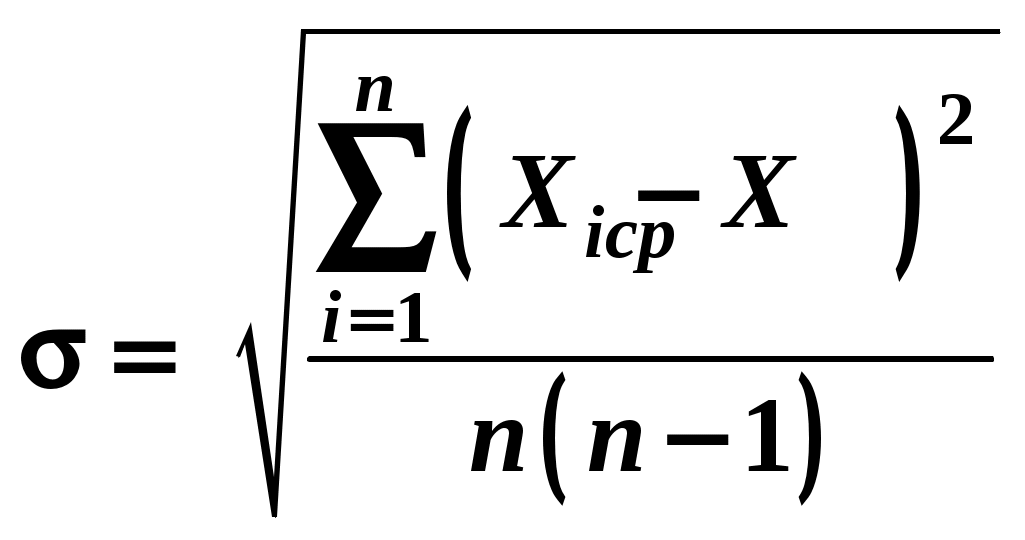можно вычислить по формуле: ,где Xср– среднее арифметическое значение всех измерений, рассчитываемое по формуле: 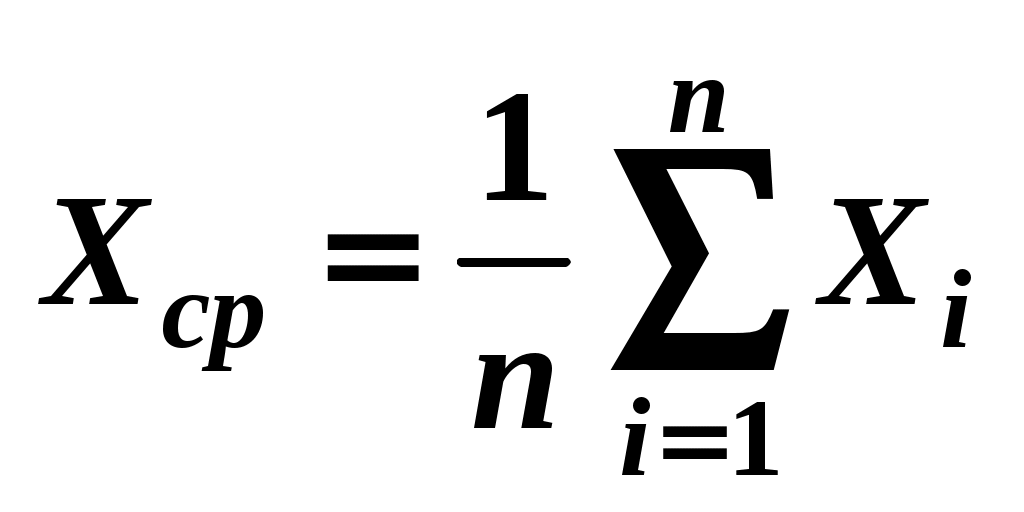.Полная абсолютная погрешность Х прямых измерений определяется как:  ,где Xсист – абсолютная систематическая погрешность, Xсл – абсолютная случайная погрешность.
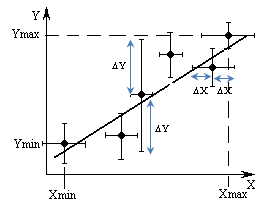
Например, а = (2,90,3) м/с2; а= 10 % с надежностью = 0,95. ОПРЕДЕЛЕНИЕ ПОГРЕШНОСТИ КОСВЕННЫХ ИЗМЕРЕНИЙ Рассмотрим методы определения погрешностей косвенных измерений. Следует учитывать, что, если в расчетах используются табличные данные (без указания погрешностей), то обычно считается, что погрешность этой величины составляет ± 0,5 разряда последней значащей цифры. Например, π = 3,14 0,005 или ускорение свободного падения g= 9,8 0,05. 1 метод. Пусть величина f является функцией нескольких переменных и ее можно представить в виде степенной функции вида 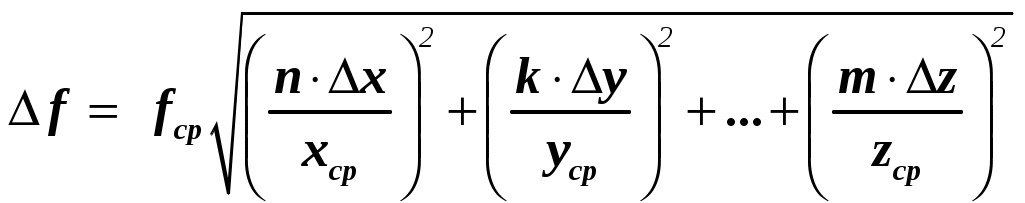 . Тогда для расчета ошибки косвенного измерения Δf можно использовать формулу (постоянные сомножители отбрасываются): ,где xср,yср, zср …– средние значения величин прямых измерений, Δx,Δy, Δz… – абсолютные ошибки этих измерений,  – среднее значение величины f.Описанную выше методику рассмотрим на примере формулы для расчета ускорения тела.  Преобразуем формулу следующим образом:  . Отбрасываем постоянный сомножитель 2. Используя формулу метода, получаем абсолютную погрешность: 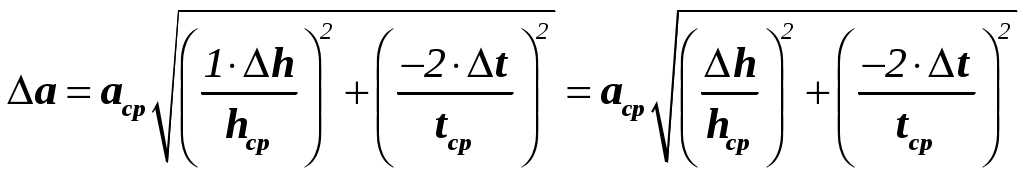 .Относительная погрешность:  .2 метод. Нахождение погрешности путем логарифмирования и последующего дифференцирования расчетной формулы. Пусть величина косвенных измерений является функцией нескольких переменных и определяется по формуле, включающей в себя сумму (разность) величин прямых измерений. Например, площадь трапеции определяется по формуле  , где h – высота, a, b – длины оснований трапеции.Для нахождения абсолютной погрешности в определении площади трапеции выполним следующую последовательность действий. а) Логарифмируем расчетную формулу  .При логарифмировании используем следующие свойства логарифмов:    .б) Дифференцируем полученное выражение, учитывая, что последнее слагаемое является функцией двух переменных:  .в) Заменяя дифференциалы соответствующими абсолютными погрешностями величин прямых измерений, возводя каждое слагаемое в квадрат и извлекая из каждой части квадратный корень, получим: 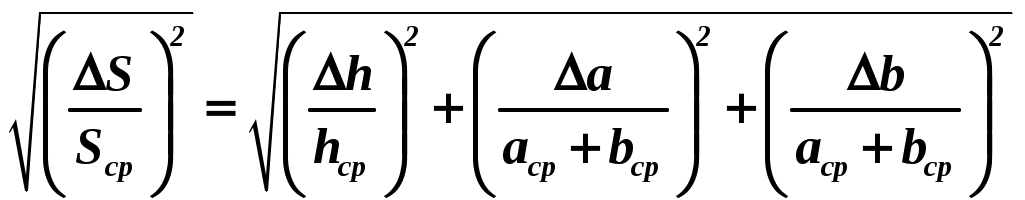 .Относительная погрешность измерений: 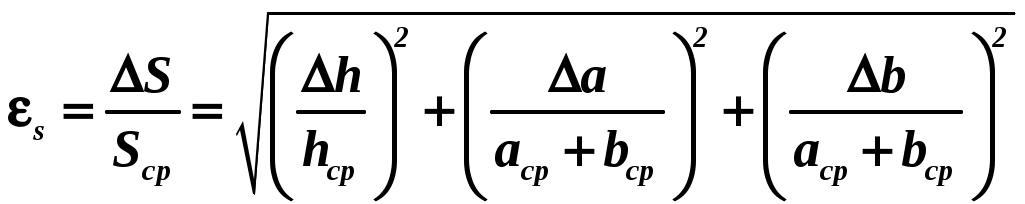 .Абсолютная погрешность измерений: 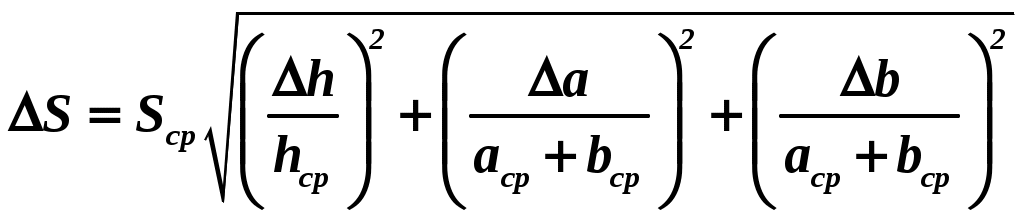 .3 метод. Определение погрешности косвенных измерений через полный дифференциал функции многих переменных с последующей заменой дифференциалов соответствующими погрешностями. Метод удобно использовать, если искомая величина является тригонометрической функцией нескольких (одной) переменных. Абсолютную ошибку косвенного измерения Δf можно вычислить по формуле: 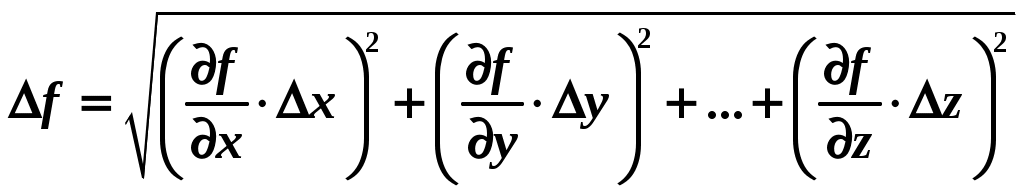 .Здесь  – частные производные функции f=f(x,y, …,z).Например, интенсивность света, прошедшего через поляризатор, определяется  . Тогда  .Абсолютная погрешность измерений:  .Погрешность в определении углов следует подставлять в радианах:  .Относительная погрешность измерений:  .ПРАВИЛА ОКРУГЛЕНИЯ ПРИ ЗАПИСИ РЕЗУЛЬТАТА Измерения всегда приводят к приближенным значениям физических величин. При проведении математических операций часто также получают приближенные значения. Приближенные числа можно округлять, если это не окажет вредного влияния на практический результат. При округлении приближенных чисел необходимо руководствоваться следующими правилами. 1. Косвенные измерения не могут быть точнее прямых измерений (количество знаков после запятой в косвенных и прямых измерениях должно быть одинаковым). В промежуточных вычислениях можно оставлять одну запасную цифру для уменьшения ошибки округления. В окончательном результате эта запасная цифра отбрасывается. 2. Если первая из отбрасываемых цифр больше или равна 5, то последняя цифра увеличивается на единицу. В противном случае последняя сохраняемая цифра не изменяется. 3. При сложении и вычитании, умножении и делении в полученном результате сохраняют столько десятичных знаков, сколько их содержится в числе с наименьшим количеством десятичных знаков. 4. В результате расчета значений функций вида xn,  результат должен содержать столько значащих цифр, сколько их имеет число x.5. В первую очередь округляют погрешность X, только затем округляют саму приближенную величинуX. После округления количество знаков после запятой в погрешности X и среднем значении величины Xср должно быть одинаковым. ГРАФИЧЕСКОЕ ПРЕДСТАВЛЕНИЕ РЕЗУЛЬТАТОВ ЭКСПЕРИМЕНТА При обработке полученного экспериментального материала для того, чтобы получить наглядное представление о зависимости одной физической величины от другой, часто прибегают к построению графиков. Графиками пользуются также для быстрого нахождения значения одной величины по данному значению другой величины. Для построения графиков чаще всего используют декартову систему координат. Графики экспериментальных зависимостей всегда строятся с учетом погрешности измерений. Основные требования, предъявляемые к построению графиков Графики строятся карандашом на миллиметровой бумаге или белой бумаге, на которую печатным способом нанесена координатная сетка. Допускается построение графиков методами компьютерной графики, но и в этом случае графики должны соответствовать всем изложенным требованиям. На координатных осях должны быть указаны обозначения откладываемых величин и единицы их измерения. Начало координат, если это оговорено особо, может не совпадать с нулевыми значениями величин. Его выбирают таким образом, чтобы площадь чертежа была использована максимально. Перед построением графика для каждой из шкал необходимо выбрать масштаб. Масштабные деления на координатных осях нужно наносить равномерно, то есть через равные промежутки. Масштаб выбирают таким образом, чтобы кривая была равномерно растянута вдоль обеих осей. Если график представляет собой прямую, то угол ее наклона к осям должен быть близок к 40о – 60о. После выбора и нанесения на оси масштаба, наносятся значения физических величин. Экспериментальные точки изображаются четко и крупно маркерами (в виде кружков, прямоугольников, крестиков и т. д.). Координаты экспериментальных точек на осях не указывают, а линии, определяющие эти координаты, не проводят, так как это загромождает график и затрудняет работу с ним. Затем от каждой точки вверх и вниз, вправо и влево откладывают в виде отрезков соответствующие абсолютные погрешности измерений в масштабе графика (рис. 1). После нанесения экспериментальных точек строится график, то есть проводится предсказанная теорией плавная кривая или прямая так, чтобы она пересекала все отложенные на графике отрезки, соответствующие абсолютным погрешностям измерений.
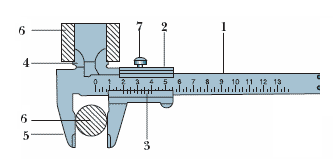
Описание штангенциркуля и методики проведения измерений линейных размеров ТЕЛ Штангенциркуль – наиболее распространенный прибор, используемый для измерения линейных размеров тел (деталей) с высокой точностью.
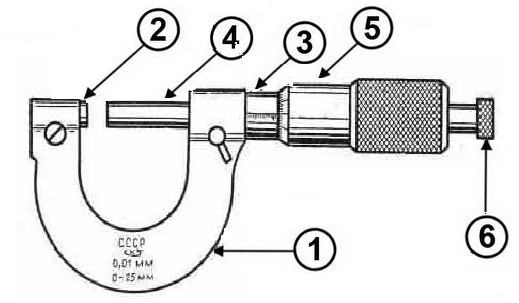
Для измерения штангенциркуль берут в правую руку, измеряемый предмет 6 помещают между ножками, придерживая его левой рукой. Надавливая на рамку большим пальцем правой руки, плотно зажимают предмет между ножками. Затем закрепляют винт и проводят отсчет по нониусу. Верхние ножки служат для определения внутренних отверстий предметов. При определении размера детали поступают следующим образом: Если нулевой штрих нониуса совпал с каким–либо штрихом штанги, то значение измеряемой величины отсчитывают только по основной шкале в миллиметрах. Если же нулевой штрих нониуса не совпадает ни с одним штрихом основной шкалы, то значение измеряемой величины складывается из двух частей: целого числа миллиметров, отсекаемых нулевым штрихом нониуса на основной шкале штанги, и долей миллиметра, полученных умножением точности нониуса на порядковый номер его ненулевого штриха, совпавшего с некоторым делением штанги (рис. 3). 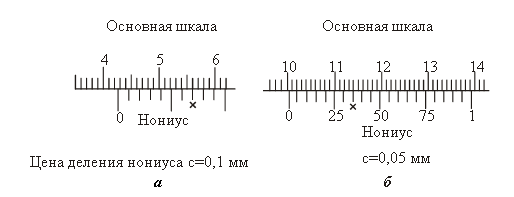 Рисунок 3 – Примеры взаимного расположения шкал штангенциркуля (а) размеры измеряемого предмета D=42 мм + 7•0,1 мм = 42,7 мм (б) размеры измеряемого предмета D=100 мм + 7•0,05 мм = 100,35 мм Описание МИКРОМЕТРА и методики проведения измерений линейных размеров ТЕЛ Микрометр представляет собой прибор, предназначенный для измерения линейных размеров с точностью до 0,01 мм.
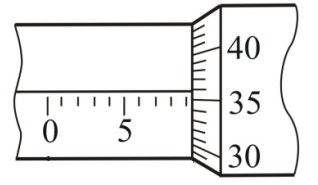
Действие микрометра основано на свойстве винта совершать при его повороте поступательное перемещение, пропорциональное углу поворота. При измерении предмет зажимается между пяткой и микрометрическим винтом. Для вращения барабана при этом пользуются фрикционной головкой.После того, как достигнута определенная степень нажатия на предмет, фрикционная головка начинает проскальзывать, издавая характерный треск. Благодаря этому, зажатый предмет деформируется сравнительно мало (его размеры не искажаются) и, кроме того, микрометрический винт предохраняется от порчи. На трубке 3нанесены деления основной шкалы.Барабан 5при вращении винта перемещается вдоль трубки. Шаг винта подбирают таким, что один полный оборот барабана соответствует его смещению вдоль основной шкалы на длину наименьшего деления. На барабане нанесена добавочная шкала.Микрометры обычно бывают двух типов. Основная шкала микрометра разбита на миллиметры.Шаг микрометрического винта также 1 мм. На шкале барабана нанесено 100 равных делений. Ясно, что каждое из этих ста делений имеет достоинство 0,01 мм,так как при повороте барабана на одно деление его шкалы происходит поступательное перемещение микрометрического винта на 0,01 мм.Если нулевое деление барабана совпадает с прямой линией на трубке (рис. 5), то микрометр показывает целое число миллиметров, которое определяется делением основной шкалы, показавшимся из–под края барабана. Если же нуль шкалы барабана не совпадает с линией на трубке, то отсчет не равен целому числу миллиметров. В этом случае число целых миллиметров определяется последним видимым делением основной шкалы, а число сотых долей миллиметра — делением шкалы барабана, стоящим против линии на трубке. На рис. 5 измеряемая длина равна 9 мм + 0,36 мм = 9,36 мм.
|
