|
|
Интегралы. Интегральное исчисление
Индивидуальное домашнее задание № 2
Тема: «Интегральное исчисление»
Вариант___
Задание 1. Определенный интеграл. Интегрирование методом замены переменной.
Вычислить определённый интеграл, заменив переменную и вычислив новые пределы интегрирования. Результат записать в виде обыкновенной дроби.
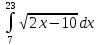
Решение:
Пусть 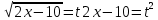
Заменим пределы интегрирования: если
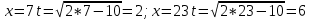 . .
Вычислим дифференциал 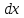 . Для его вычисления используем равенство . Для его вычисления используем равенство 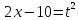 — если равны функции, то равны и их дифференциалы: — если равны функции, то равны и их дифференциалы:
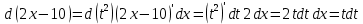
Составим интеграл по переменной 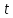 , эквивалентный исходному, и вычислим его значение: , эквивалентный исходному, и вычислим его значение:
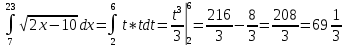
Ответ: 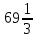
Задание 2. Интегрирование рациональных функций.
Вычислить определённый интеграл от рациональной функции, разложив её на элементарные дроби. Результат округлить с точностью до 0,001.
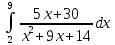
Решение:
1) Представим подынтегральную функцию в виде суммы элементарных дробей. Для этого вначале вычислим корни многочлена в знаменателе.
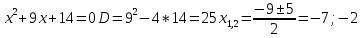
Т.о., многочлен можно представить в виде произведения: 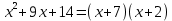
Представим подынтегральную функцию в виде суммы двух элементарных дробей с неопределёнными коэффициентами:
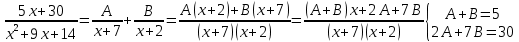
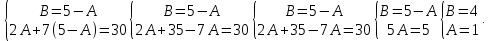
Т.о., подынтегральная рациональная функция примет вид: 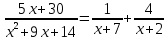
2) В исходном интеграле заменим подынтегральную функцию и вычислим определённый интеграл с заданной точностью:
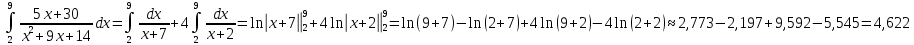
Ответ: 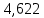
-Задание 3. Определенный интеграл. Площадь криволинейной трапеции.
Определить площадь криволинейной трапеции, ограниченной линиями. Пределы интегрирования определить аналитически. Выполнить чертёж в заданном масштабе: за единичный отрезок взять 1 клетку. Результат представить в виде обыкновенной дроби и десятичной дроби с точностью до 0,001.
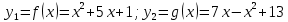
Решение:
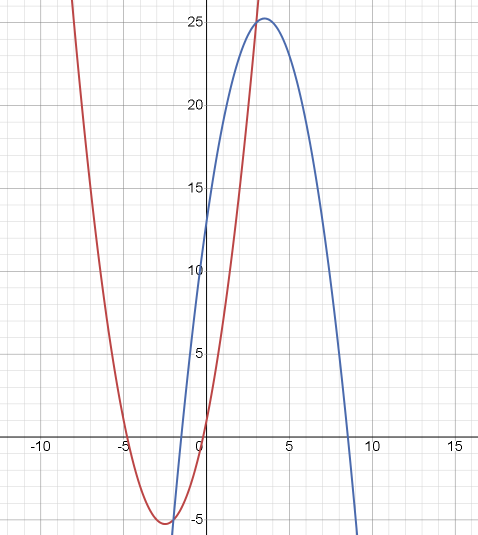
1) Построение.
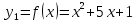 — парабола с вершиной в точке с координатами (-2,5; -5,25). Ветви параболы направлены вверх. — парабола с вершиной в точке с координатами (-2,5; -5,25). Ветви параболы направлены вверх.
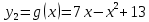 — парабола с вершиной в точке с координатами (3,5;25,25). Ветви параболы направлены вниз. — парабола с вершиной в точке с координатами (3,5;25,25). Ветви параболы направлены вниз.
2) Вычислим аналитически пределы интегрирования:
Пределы интегрирования – это абсциссы точек пересечения парабол.
Абсциссы точек пересечения:
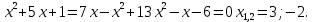
3) Составим интегральное уравнение площади искомой фигуры и вычислим определённый интеграл: {в подынтегральной функции из уравнения верхней кривой вычитаем уравнение нижней кривой}
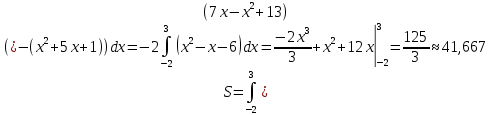
Ответ: 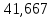
Задание 4. Интеграл в физических задачах. Кинематика.
Скорость тела изменяется по закону 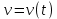 . Определить путь, пройденный телом за интервал времени от . Определить путь, пройденный телом за интервал времени от 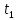 до до 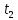 . .
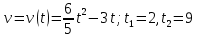
Решение:
Если тело движется с переменной скоростью, то путь, пройденный телом от момента времени 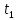 до момента времени до момента времени 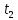 будет равен интегралу: будет равен интегралу:
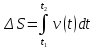
Составим интегральное уравнение пройденного пути и вычислим определенный интеграл:
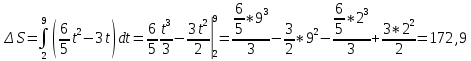
Ответ: 172,9
Задание 5. Интеграл в физических задачах. Работа переменной силы.
Вдоль оси 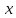 действует переменная сила действует переменная сила 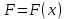 . Определить работу этой силы на участке траектории от . Определить работу этой силы на участке траектории от 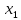 до до 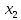 . Результаты вычислений округлить до 0,001. . Результаты вычислений округлить до 0,001.
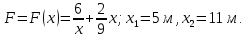
Решение:
Если на тело действует переменная сила 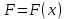 , то работа этой силы на интервале от , то работа этой силы на интервале от 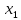 до до 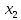 будет равна интегралу: будет равна интегралу:
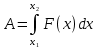
Составим интегральное уравнение работы и вычислим определённый интеграл:
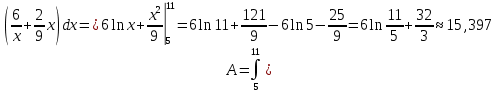
Ответ: 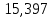 Дж Дж
Задание 6. Интеграл в физических задачах. Электродинамика.
Вычислить электрический заряд, переносимый за интервал времени от 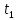 до до 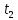 секунд через поперечное сечение проводника, если сила тока меняется по закону секунд через поперечное сечение проводника, если сила тока меняется по закону 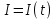 . Результаты вычислений округлить до 0,001. . Результаты вычислений округлить до 0,001.
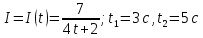
Решение:
Если по проводнику течёт переменный ток, уравнение которого 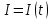 , то за интервал времени от , то за интервал времени от 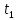 до до 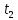 секунд через поперечное сечение проводника пройдёт заряд, равный интегралу: секунд через поперечное сечение проводника пройдёт заряд, равный интегралу:
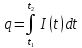
Составим интегральное уравнение и вычислим определённый интеграл:
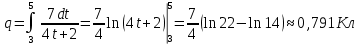
Ответ: 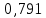 Кл Кл
Задание 7. Интеграл в физических задачах. Работа и мощность.
Мощность силовой установки в кВт зависит от времени согласно следующему закону: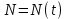 . .
Определить работу в кДж, выполняемую этой установкой за время от 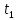 до до 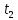 . Время задано в секундах. Результаты вычислений округлить до 0,001. . Время задано в секундах. Результаты вычислений округлить до 0,001.
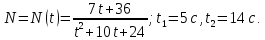
Решение.
Работа, выполняемая силовой установкой, будет равна интегралу:
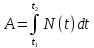
Составим интегральное уравнение работы:
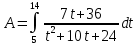
Подынтегральная функция является дробно-рациональной. (Пошаговый алгоритм решения подобных интегралов в Задании 2)
Представим подынтегральную функцию в виде суммы элементарных дробей.
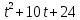 — корни квадратного уравнения найдём с помощью теоремы Виета. — корни квадратного уравнения найдём с помощью теоремы Виета.
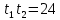 и и 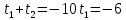 и и 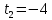 . .
Т.о. многочлен в знаменателе можно представить в виде произведения
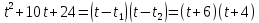
Подынтегральная функция примет вид: 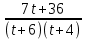 . Представим её в виде суммы элементарных дробей. Используем метод неопределённых коэффициентов для вычисления числителей элементарных дробей: . Представим её в виде суммы элементарных дробей. Используем метод неопределённых коэффициентов для вычисления числителей элементарных дробей:
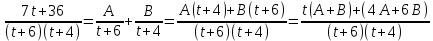
Сравнивая слагаемые числителя, составим систему:
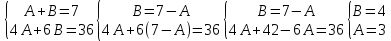
Т.о., подынтегральная функция в виде суммы двух элементарных дробей примет вид:
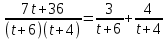
В исходном интеграле заменим подынтегральную функцию и вычислим значение определённого интеграла:
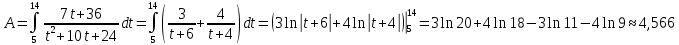
Ответ: 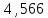 кДж кДж
-Задание 8. Объём тела вращения.
График функции 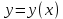 вращается вокруг оси вращается вокруг оси 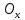 . Определить объём тела вращения в диапазоне . Определить объём тела вращения в диапазоне 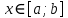 . Результаты вычислений округлить до 0,001. Изобразить график заданной функции в прямоугольной системе координат . Результаты вычислений округлить до 0,001. Изобразить график заданной функции в прямоугольной системе координат 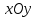 . .
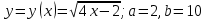
Решение.
График функции 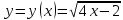 : :
Область определения функции: 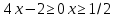 заданный интервал заданный интервал 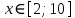 входит в область определения. входит в область определения.
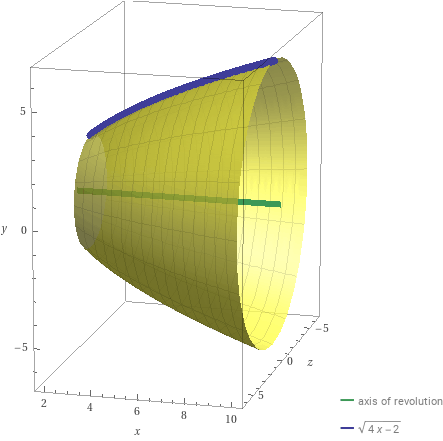
Составим интегральное уравнение для вычисления объёма полученного тела вращения.
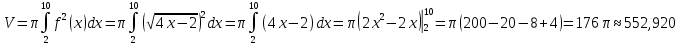
Ответ:  куб. ед. куб. ед.
Индивидуальное домашнее задание № 2. Тема: «ИНТЕГРАЛЬНОЕ ИСЧИСЛЕНИЕ».
|
|
|
 Скачать 138.19 Kb.
Скачать 138.19 Kb.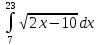
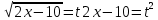
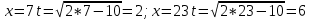 .
.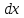 . Для его вычисления используем равенство
. Для его вычисления используем равенство 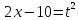 — если равны функции, то равны и их дифференциалы:
— если равны функции, то равны и их дифференциалы: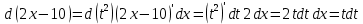
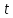 , эквивалентный исходному, и вычислим его значение:
, эквивалентный исходному, и вычислим его значение: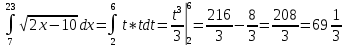


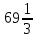
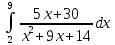
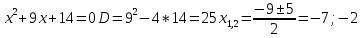
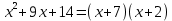
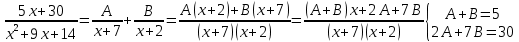
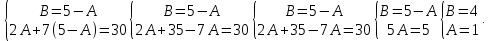
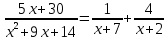
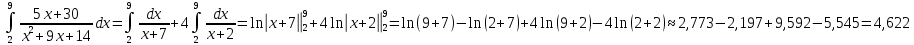
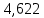
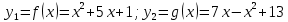
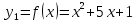 — парабола с вершиной в точке с координатами (-2,5; -5,25). Ветви параболы направлены вверх.
— парабола с вершиной в точке с координатами (-2,5; -5,25). Ветви параболы направлены вверх.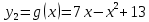 — парабола с вершиной в точке с координатами (3,5;25,25). Ветви параболы направлены вниз.
— парабола с вершиной в точке с координатами (3,5;25,25). Ветви параболы направлены вниз. 
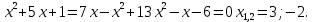
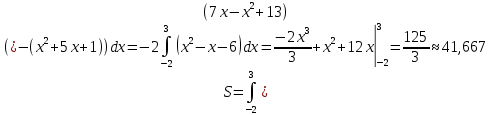
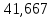
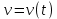 . Определить путь, пройденный телом за интервал времени от
. Определить путь, пройденный телом за интервал времени от 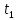 до
до 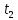 .
.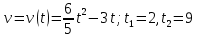
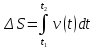
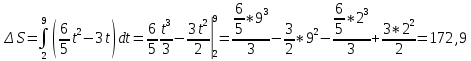
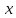 действует переменная сила
действует переменная сила 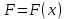 . Определить работу этой силы на участке траектории от
. Определить работу этой силы на участке траектории от 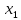 до
до 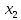 . Результаты вычислений округлить до 0,001.
. Результаты вычислений округлить до 0,001.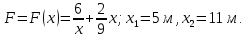
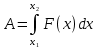
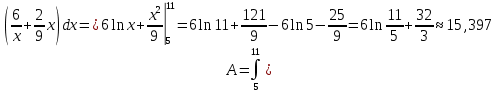
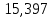 Дж
Дж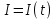 . Результаты вычислений округлить до 0,001.
. Результаты вычислений округлить до 0,001.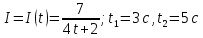
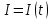 , то за интервал времени от
, то за интервал времени от 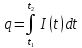
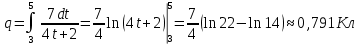
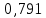 Кл
Кл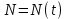 .
.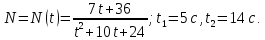
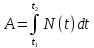
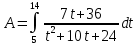
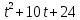 — корни квадратного уравнения найдём с помощью теоремы Виета.
— корни квадратного уравнения найдём с помощью теоремы Виета.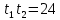 и
и 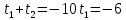 и
и 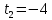 .
.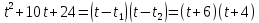
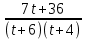 . Представим её в виде суммы элементарных дробей. Используем метод неопределённых коэффициентов для вычисления числителей элементарных дробей:
. Представим её в виде суммы элементарных дробей. Используем метод неопределённых коэффициентов для вычисления числителей элементарных дробей: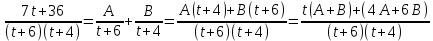
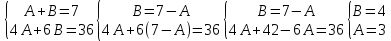
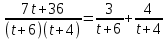
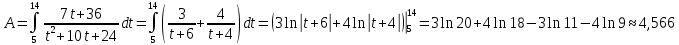
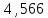 кДж
кДж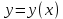 вращается вокруг оси
вращается вокруг оси 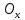 . Определить объём тела вращения в диапазоне
. Определить объём тела вращения в диапазоне 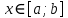 . Результаты вычислений округлить до 0,001. Изобразить график заданной функции в прямоугольной системе координат
. Результаты вычислений округлить до 0,001. Изобразить график заданной функции в прямоугольной системе координат 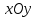 .
.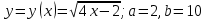
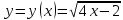 :
: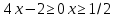 заданный интервал
заданный интервал 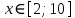 входит в область определения.
входит в область определения.
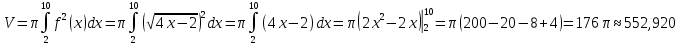
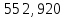 куб. ед.
куб. ед.