Ильина1_Агишев2_RM5. Интеллектуальный анализ данных
 Скачать 0.73 Mb.
|
|
Федеральное государственное бюджетное общеобразовательное учреждение высшего образования «Уфимский государственный авиационный технический университет» Факультет информатики и робототехники Кафедра вычислительной математики и кибернетики Отчет к лабораторной работе №5 по дисциплине «Интеллектуальный анализ данных» Выполнили студенты гр. МО-411 Агишев С.Б. Ильина А.В. Проверил ст. преподаватель каф. ВМиК Харисова Э.А. Уфа 2019 Задачи Задание 1 Сгенерируйте вектор длины N=1000, элементами которого являются реализации нормально распределенной случайной величины с математическим ожиданием, равным 1, и стандартным отклонением, равным 0.3. Подсчитайте статистическое мат. ожидание и стандарную ошибку, не используя встроенные функции и проверьте правильность результата. Подсчитайте .95,.99-квантили. Исследуйте отклонение статистического мат. ожидания от 1 при росте N (N=1000,2000,4000,8000). Код задачи Сгенерируем вектор длины N=1000, элементами которого являются реализации нормально распределенной случайной величины с математическим ожиданием, равным 1, и стандартным отклонением, равным 0.3. vect = rnorm (n=1000,mean=1,sd=0.3) Подсчитаем статистическое мат. ожидание как сумму элементов вектора деленую на его длину mean_ = sum(vect)/length(vect) Посчитаем дисперсию variance_ = 0 for (i in 1:length(vect)) { variance_ = variance_ + (vect[i] - mean_) ^ 2 } variance_ = variance_ / length(vect) Найдем случайное отклонение как корень из дисперсии standard_deviation_ = sqrt(variance_) Найдем стандартную ошибку как отношение величины среднеквадратического отклонения генеральной совокупности, к корню из объёма выборки. standard_error_ = standard_deviation_ / sqrt(length(vect)) Выведем полученные результаты, паралелльно сравнив с результатами полученными при использовании встроенных функций cat("Mean: my = ", mean_, " should be = ", mean(vect)) print("") cat("Variance: my = ", variance_, " should be = ", var(vect)) print("") cat("standard_deviation: my = ", standard_deviation_, " should be = ", sd(vect)) print("") cat("standard_error: my = ", standard_error_, " should be = ", sd(vect)/sqrt(length(vect))) print("") Подсчитаем .95,.99-квантили print(quantile(vect, c(.95, .99))) Исследуем отклонение статистического мат. ожидания от 1 при росте N (N=1000,2000,4000,8000). Чтобы более наглядно изучить этот вопрос введем рост N с меньшей величины. for (i in c(2, 10, 50, 300, 1000, 2000, 4000, 8000)) { зададим вектор из элементов, распределенных нормально vect <- rnorm (i,mean=1,sd=0.3) cat("Vector length = ", length(vect), " sd = ", sd(vect) - 1) print("") } Результаты 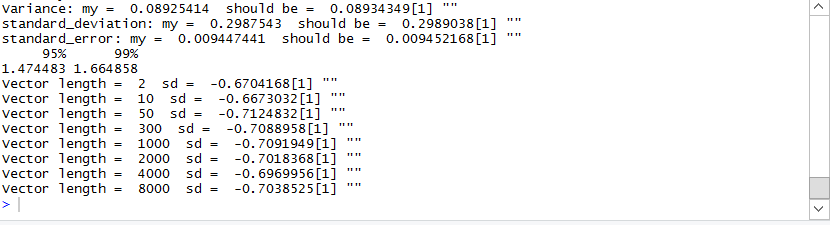 Рисунок 1 –Результат работы программы Как видно из рис.1 подсчитанные нами значения дисперсии, стандартного отклонения, стандартной ошибки совпадают с соответствующими значениями, подсчитанными с помощью встроенных функций. При росте длины вектора мы наблюдаем незначительное изменение мат. ожидания. Задание 2 Создайте фрейм данных из N=20 записей со следующими полями: Nrow — номер записи, Name — имя пользователя, BirthYear — год рождения, EmployYear — год приема на работу, Salary — зарплата, где Nrow изменяется от 1 до N, Name задается произвольно, BithYear распределен равномерно на отрезке [1960,1985], EmployYear распределен равномерно на отрезке [BirthYear+18,2006], Salary для работников младше 1975 г.р. определяется по формуле Salary=(ln(2007-EmployYear)+1)*8000, для остальных Salary=(log2(2007-EmployYear)+1)*8000. Подсчитайте число сотрудников с зарплатой, большей 15000. Добавьте в таблицу поле, соответствующее суммарному подоходному налогу (ставка 13%), выплаченному сотрудником за время работы в организации, если его зарплата за каждый код начислялась согласно формулам для Salary, где вместо 2007 следует последовательно подставить каждый год работы сотрудника в организации. Код задачи Создаем фрейм данных Employees <- data.frame(Nrow = integer(), Name = character(), BirthYear = integer(), EmployYear = integer(), Salary = double(), stringsAsFactors = FALSE) Функция для расчета з/п сотрудника getSalary <- function(birthYear, employYear, currentYear) { для работников младше 1975 г.р. if(birthYear > 1975) { З/п определяется по формуле: return ((log(currentYear - employYear) + 1) * 8000) } Для остальных else { return ((log2(currentYear - employYear) + 1) * 8000) } } Задаем кол-во записей N = 20 for(i in 1:N) { BithYear распределен равномерно на отрезке [1960,1985] BirthYear0 = floor(runif(n = 1, min = 1960, max = 1985 + 1)) EmployYear0 = floor(runif(n = 1, min = BirthYear0 + 18, max = 2006 + 1)) Salary0 = getSalary(BirthYear0, EmployYear0, 2007) Salary0 = round(Salary0, digits = 3) Employees <- rbind(Employees, data.frame(Nrow = i, Name = paste("name", i), BirthYear = BirthYear0, EmployYear = EmployYear0, Salary = Salary0)) } salaryMore15KCounter = 0 Подсчитаем число сотрудников с зарплатой, большей 15000 for(i in 1:nrow(Employees)) { if (Employees$Salary[i] > 15000) { salaryMore15KCounter = salaryMore15KCounter + 1 } } Добавление в таблицу поля, соответствующего суммарному подоходному налогу (ставка 13%) Employees$"13%" <- 0 for(i in 1:nrow(Employees)) { total_salary = 0 for(currentYear in (EmployYear0 + 1):2007) { birthYear = Employees$BirthYear[i] employYear = Employees$EmployYear[i] salary = getSalary(birthYear, employYear, currentYear) total_salary = total_salary + salary } Employees$`13%`[i] = total_salary * (1 - 0.13) } Печать результата print(Employees) Результаты  Рисунок 2 – Результат работы программы Задание 3 Напишите функцию, которая принимает на вход числовой вектор x и число разбиений интервала k (по умолчанию равное числу элементов вектора, разделенному на 10) и выполняет следующее: находит минимальное и максимальное значение элементов вектора xmin и xmax, разделяет полученный отрезок [xmin;xmax] на k равных интервалов и подсчитывает число элементов вектора, принадлежащих каждому интервалу. Далее должен строиться график, где по оси абсцисс — середины интервалов, по оси ординат — число элементов вектора, принадлежащих интервалу, разделенное на общее число точек. Проведите эксперимент на данной функции, где x — вектор длины 5000, сгенерированный из экспоненциально распределенной случайной величины, k=500. Приближение какого графика мы получаем в итоге при большом числе точек и числе разбиений? Код задачи fun3 <- function(x, k = length(x) / 10) { xmin = min(x) xmax = max(x) t = hist(x, freq = FALSE, breaks = k, plot = FALSE) h = hist(x, freq = FALSE, breaks = k, xaxt = 'n', xlab = axis(side=1, at=t$mids)) } # v = rexp(5000, 0.3) # fun3(v) # fun3(v, 20) Результаты  Рисунок 3 - эксперимент на данной функции, где x — вектор длины 5000 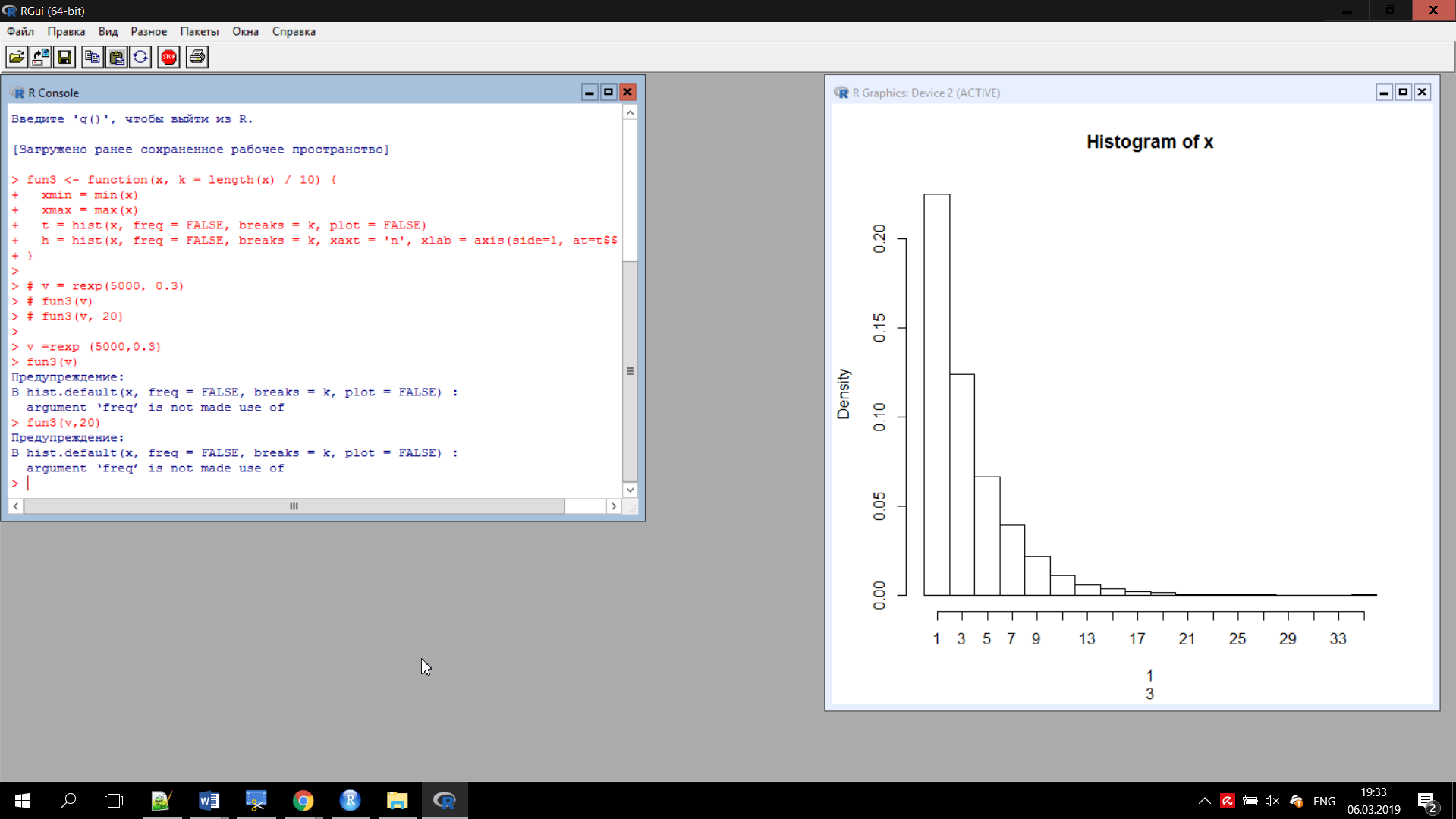 Рисунок 4 - эксперимент на данной функции, где x — вектор длины 20 Задание 4 Спроектируйте и реализуйте метод наименьших квадратов. Суть метода наименьших квадратов (МНК). З  адача заключается в нахождении коэффициентов линейной зависимости, при которых функция двух переменных, а и b принимает наименьшее значение. То есть, при данных а и b сумма квадратов отклонений экспериментальных данных от найденной прямой будет наименьшей. В этом вся суть метода наименьших квадратов. Таким образом, решение примера сводится к нахождению экстремума функции двух переменных Вывод формул для нахождения коэффициентов. Составляется и решается система из двух уравнений с двумя неизвестными. Находим частные производные функции 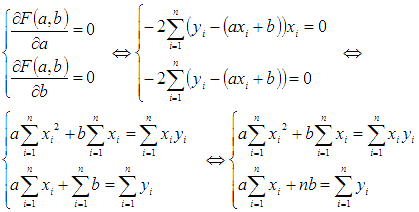 по переменным а и b, приравниваем эти производные к нулю. Решаем полученную систему уравнений любым методом (например, методом подстановки или методом Крамера) и получаем формулы для нахождения коэффициентов по методу наименьших квадратов (МНК).  При данных а и b функция принимает наименьшее значение. Формула для нахождения параметра a содержит суммы  ,  ,  ,  и параметр n - количество экспериментальных данных. Коэффициент b находится после вычисления a.Код задачи Сгенерируем такой набор данных x, y на котором наглядно можно продемонстрировать МНК. (Но мы понимаем, что метод не завязан на свойствах исходных данных, он работает с произвольными инпутами). x <- runif(n=500, 0, 100) y <- x for (i in 1:length(y)) { y[i] <- 0.8 * y[i] + 10 * rnorm(n=1, mean = 0, sd = 1) } prefix_sums <- function(x) { n <- length(x) result <- rep(0, n) t_sum = 0 for (i in 1:i) { t_sum <- t_sum + x[i] result[i] = t_sum } return(result) } row1 <- prefix_sums(x) row2 <- prefix_sums(y) row3 <- prefix_sums(x * y) row4 <- prefix_sums(x * x) # print(row1) # print(row2) # print(row3) # print(row4) getA <- function(x, y) { n <- length(x) q1 <- n * sum(x * y) q2 <- sum(x) * sum(y) q3 <- n * sum(x * x) q4 <- sum(x) ^ 2 a <- (q1 - q2)/(q3 - q4) return(a) } getB <- function(x, y, a) { n <- length(x) q1 <- sum(y) q2 <- a * sum(x) b <- (q1 - q2) / n return(b) } a = getA(x, y) b = getB(x, y, a) print(a) print(b) plot(x, y) abline(b, a) Результаты 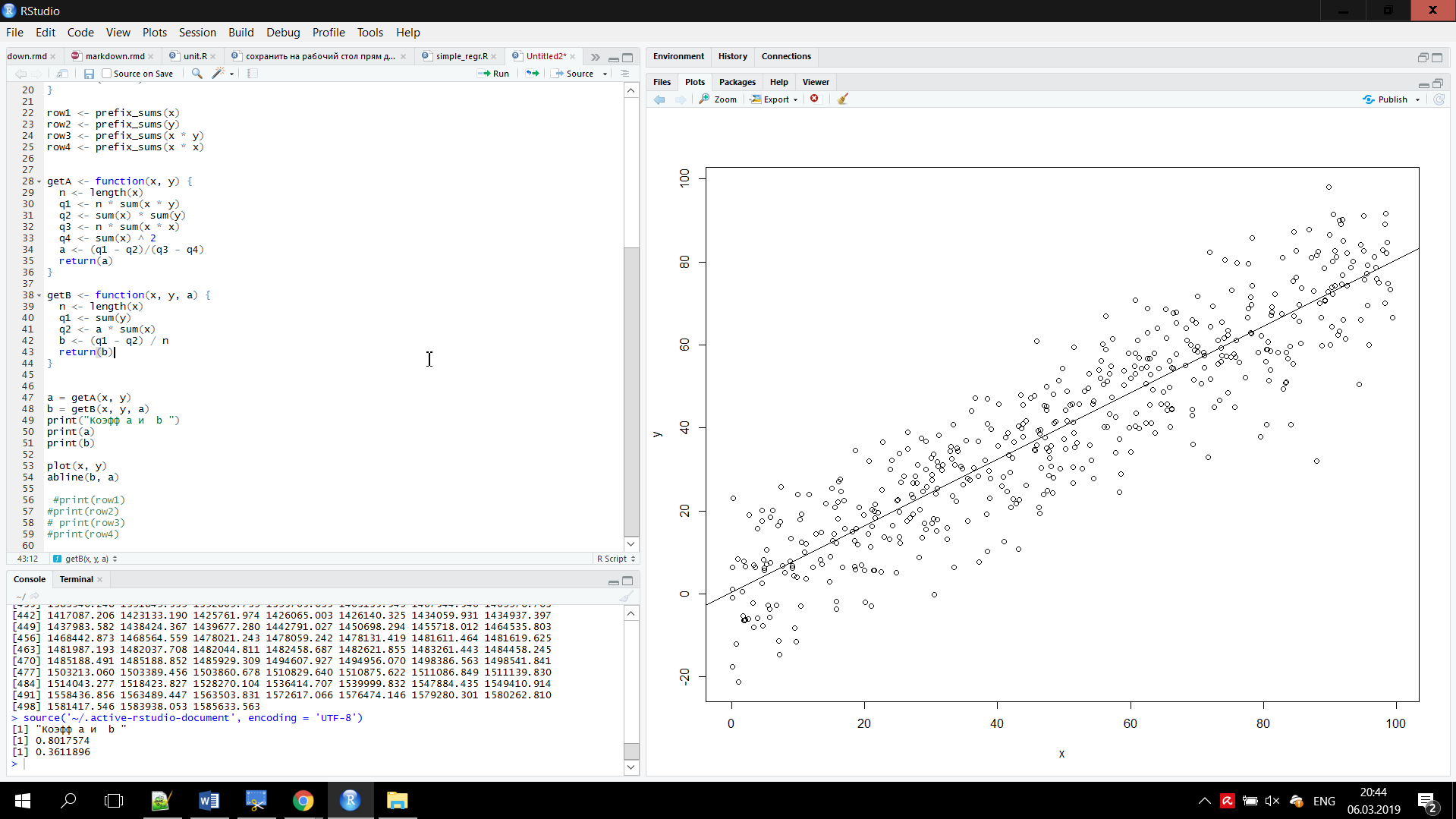 Рисунок 5 –Результат работы МНК |