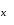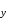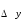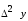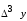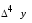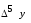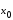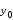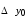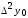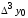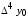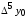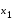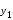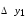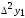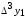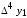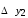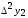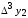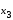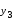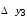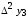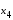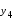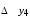Лагранж решение. Интерполяция функции
 Скачать 109.56 Kb. Скачать 109.56 Kb.
|
|
ИНТЕРПОЛЯЦИЯ ФУНКЦИИ Результаты экспериментов обычно бывают представлены ограниченным числом в виде таблиц, отражающих зависимость величины исследуемого явления y от фактора x. При этом величины 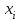 , где , где 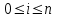 , образуют , образуют 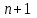 узловую точку. Для практического применения, как правило, необходимо знать и промежуточные, по отношению к табличным, значения y. узловую точку. Для практического применения, как правило, необходимо знать и промежуточные, по отношению к табличным, значения y.Если бы была известна форма зависимости 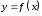 , то это означало бы, что любому значению x из области определения поставлено в соответствие значение y. Но на практике явная связь между y и x обычно неизвестна, поэтому возникает необходимость приближенной замены данной функции , то это означало бы, что любому значению x из области определения поставлено в соответствие значение y. Но на практике явная связь между y и x обычно неизвестна, поэтому возникает необходимость приближенной замены данной функции 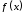 некоторой функцией некоторой функцией 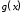 . Процедура нахождения функции . Процедура нахождения функции 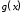 для данной функции для данной функции 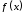 называется приближением функций. Одним из способов выбора приближения функции и является интерполяция. Интерполяция есть восстановление функции (точное или приближенное) по известным ее значениям. называется приближением функций. Одним из способов выбора приближения функции и является интерполяция. Интерполяция есть восстановление функции (точное или приближенное) по известным ее значениям. Если интерполирующая функция 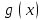 строится на всем интервале изменения аргумента строится на всем интервале изменения аргумента 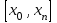 , то такая интерполяция называется глобальной. , то такая интерполяция называется глобальной.Если интерполяционные многочлены строятся отдельно для разных частей рассматриваемого интервала изменения x, то говорят о локальной интерполяции. В тех случаях, когда интерполяционные многочлены используются для приближенного вычисления функции вне рассматриваемого отрезка 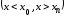 , приближение функции называют экстраполяцией. , приближение функции называют экстраполяцией.Интерполирующая функция 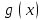 принимает в узлах принимает в узлах 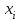 те же значения те же значения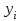 , что и функция , что и функция 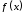 , т.е. , т.е. 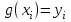 , i = 0, 1, …, n. (4.12) , i = 0, 1, …, n. (4.12)Выражение для 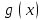 выбирают так, чтобы оно позволяло достаточно легко вычислять значения интерполирующей функции. После этого полагают выбирают так, чтобы оно позволяло достаточно легко вычислять значения интерполирующей функции. После этого полагают 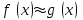 для всех x из для всех x из 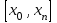 . Чаще всего . Чаще всего 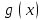 представляют в виде полинома, максимальная степень которого при числе узлов представляют в виде полинома, максимальная степень которого при числе узлов 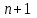 составляет n: составляет n: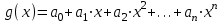 . (4.13) . (4.13)Примером глобальной интерполяции могут служить многочлены Ньютона и Бесселя, рассмотренные ниже для случая равноотстоящих значений аргумента, т.е. шаг 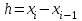 = const (i = 1, 2, …, n). = const (i = 1, 2, …, n).Интерполяция полиномами Ньютона Первая интерполяционная формула Ньютона (или интерполяционный многочлендля интерполирования вперед) имеет вид: 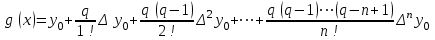 , (4.14) , (4.14)где 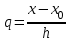 , , 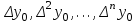 - конечные разности. - конечные разности.Разности первого порядка функции есть: 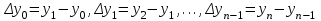 . .Разности второго порядка функции: 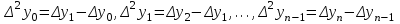 . .Аналогично составляются разности порядка k: 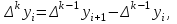 i = 0, 1,…, n-1. i = 0, 1,…, n-1.Для удобства конечные разности обычно представляют в виде таблицы, в которую выписываются также значения аргумента x и функции y. Такую таблицу называют таблицей разностей (см. табл. 4.10). Таблица 4.10 Таблица конечных разностей
Вторая интерполяционная формула Ньютона (или интерполяционный многочлендля интерполирования назад) записывается в виде: 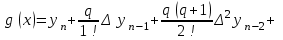 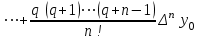 , (4.15) , (4.15)где 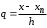 . .Выбор исходной формулы выполняется следующим образом. Для вычисления значения функции в точках левой половины рассматриваемого отрезка 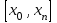 используется формула (4.14), для вычисления функции в точках правой половины отрезка используется формула (4.14), для вычисления функции в точках правой половины отрезка 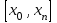 - формула (4.15). - формула (4.15).Формулы Ньютона удобно применять, если количество узлов интерполяции постепенно увеличивается. При этом учет нового узла требует лишь вычисления одного дополнительного слагаемого в (4.14) и (4.15). Вариант 4 Решенние:  Выводы: Искомое промежуточное, по отношению к табличному, значение давления насыщенного параPпри температуре T= 24oС, рассчитанное по первой интерполяционной формуле Ньютона, равно Q(105 oС) = 2243,91 кДж/кГ, второй интерполяционной формуле Ньютона, равно Q(105 oС) = 2243,91 кДж/кГ. Как видим, результаты с точностью округлений совпадают. Результаты эксперимента – исследование термодинамических свойств воды и водяного пара в состоянии насыщения - представлены в таблице. Решение: Интерполяционная формула Лагранжа (одна из формул, применяемая для не равноотстоящих узлов): Будем искать интерполяционный многочлен в виде линейной комбинации многочленов степени n: 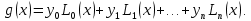 Формула интерполяционного многочлена Лагранжа: 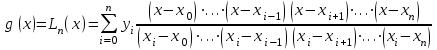 . (4.16 . (4.16n = 4 Подставляя в формулу x=Т= 105, получим : Вывод: Посчитал по формуле Лангранжа получилось 2244,02 Кдж/кг что совпадает с формулой Ньютона 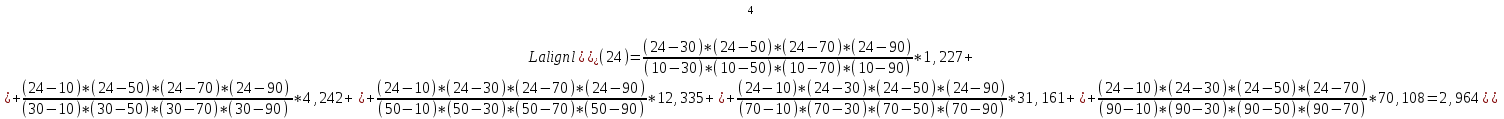 |