Прикладная физика в электроэнергетике. ЭПбз-18-2 49 Маризов А.А.. Иркутский национальный исследовательский

• Название: Иркутский национальный исследовательский
• Анкор: Прикладная физика в электроэнергетике
• Дата: 13.03.2022
• Размер: 1.38 Mb.
• Имя файла: ЭПбз-18-2 49 Маризов А.А..docx
• Тип: Документы; #394100
• страница: 1 из 3

Министерство науки и высшего образования Российской Федерации

Федеральное государственное бюджетное образовательное учреждение

высшего образования

ИРКУТСКИЙ НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ

ТЕХНИЧЕСКИЙ УНИВЕРСИТЕТ

Институт Энергетики

Кафедра электрических станций, сетей и систем


ИНДИВИДУАЛЬНОЕ ЗАДАНИЕ

по дисциплине

«Прикладная физика в электроэнергетике»

1.031.00.00 – ПЗ

обозначение документа

Выполнил студент		ЭПбз-18-2					А.А. Маризов
		шифр		подпись			И.О. Фамилия
Нормоконтроль							Е.В. Болоев
				подпись			И.О. Фамилия

Иркутск 2021 г.

Законы постоянного тока

Задача 1.1

Определить заряд Q, прошедший по проводу с сопротивлением R=3,01Ом при равномерном нарастании напряжения на концах провода от U₀=2,97В до U =4,31В в течение t=20,74 с.

Решение

Так как сила тока в проводе изменяется, то воспользоваться для подсчёта заряда формулой Q=It нельзя. Поэтому возьмём дифференциал заряда dQ=Idt и проинтегрируем: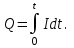

(1)

Выразив силу тока по закону Ома, получим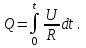

(2)

Напряжение U в данном случае переменное. В силу равномерности нарастания оно может быть выражено формулой

U= U₀+kt, (3)

где k - коэффициент пропорциональности. Подставив это выражение U в формулу (2), найдём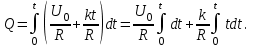



Проинтегрировав, получим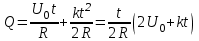

(4)

Значение коэффициента пропорциональности k найдём из формулы (3), если заметим, что при t= 20.74 с U=4.31 В: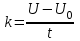





k=0,06B/c.

Подставив значения величин вформулу (4), найдём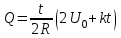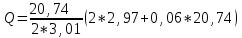





Q=25,08 Кл.

Задача 1.2

Потенциометр с сопротивлением R= 103,72Ом подключён к источнику тока, ЭДС ε которого равна 156,11 В и внутреннее сопротивление r= 50,92 Ом (рис. 1.1). Определить показание вольтметра с сопротивлением R_B=506,27 Ом, соединённого проводником с одной из клемм потенциометра и подвижным контактом с серединой обмотки потенциометра. Какова разность потенциалов между теми же точками потенциометра при отключённом вольтметре?

Р 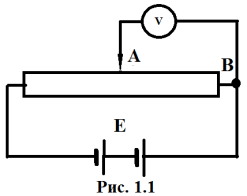ешение

Показание U₁ вольтметра, подключённого к точкам А и В, определяется по формуле

U₁=I₁R₁, (1)

где I₁ - сила тока в неразветвленной, части цепи; R₁- сопротивление параллельно соединённых вольтметра и половины потенциометра.

Силу тока I₁ найдём по закону Ома для всей цепи:

I₁=ε/(R+r), (2)

где R - сопротивление внешней цепи.

Внешнее сопротивление R есть сумма двух сопротивлений:

R=R/2+R₁. (3)

Сопротивление R₁параллельного соединения может быть найдено по формуле 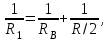откуда R_l= RR_B/(R + 2R_B).

Подставив в эту формулу числовые значения величин, и произведя вычисления, найдём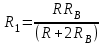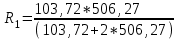





R_l=47.04 Ом.

Подставив в выражение (2) правую часть равенства (3), определим силу тока: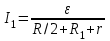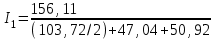





I₁=1,04 A

Если подставить значения I₁ и R₁в формулу (1), то найдём показание вольтметра:

U₁=I₁R₁

U₁=1,04*47,04

U₁=48,92В.

Разность потенциалов между точками А и В при отключённом вольтметре равна произведению силы тока I₂ на половину сопротивления потенциометра, т. е. U₂ =I₂(R/₂), или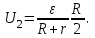

Подставив сюда значения величин ε, rи R получим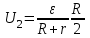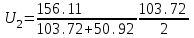





U₂=52.35 В.

Задача 1.3

С 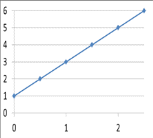ила тока в проводнике сопротивлением R=21,92 Ом нарастает в течение времени Δt=3,94 с по линейному за. кону от I₀=2,16 до I_max=8,33 А (рис. 1.2). Определить количество теплоты Q₁, выделившееся в этом проводнике за первую секунду, и Q₂ - за оставшееся время, а также найти отношение этих количеств теплоты Q₂/Q₁.

Рис.1.2

Решение

Закон Джоуля - Ленца Q= I²Rt применим в случае постоянного тока (I=const). Если же сила тока в проводнике изменяется, то указанный закон справедлив для бесконечно малого промежутка времени и записывается в виде

dQ= I²Rdt. (1)

Здесь сила тока I является некоторой функцией времени. В нашем случае

I= I₀+kt, (2)

где k - коэффициент пропорциональности, равный отношению приращений силы тока к интервалу времени, за который произошло это приращение:

k=ΔI/Δt.

k=( I_max - I₀ ) / Δt=(8.33-2.16) /3.94

k= 1,57 с

С учётом равенства (2) формула (1) примет вид

dQ=R (I₀+kt)² dt. (3)

Для определения количества теплоты, выделившегося за конечный промежуток времени Δt, выражение (3) следует проинтегрировать в пределах от t₁до t₂: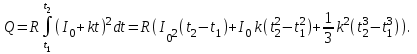



При определении количества теплоты, выделившегося за первую секунду, пределы интегрирования t₁=0, t₂= 1 с и, следовательно,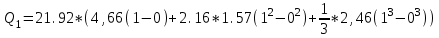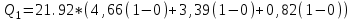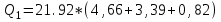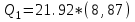









Q₁=194,43 Дж,

а за оставшееся время - пределы интегрирования t₁= 1 с, t₂= Δt с и тогда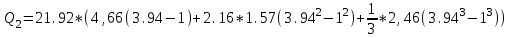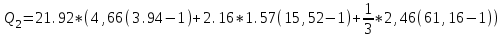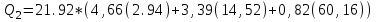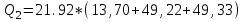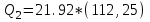











Q₂=2460,52 Дж.

Следовательно,

Q₂/Q₁=2460,52 / 194,43 =12,65 Дж,

т. е. за оставшееся время выделится теплоты в 12,65 раз больше, чем за первую секунду.

Постоянный ток в проводящей среде

Задача 2.1

Ток I, равный 17,73 А, течёт по проводнику длиной l, изготовленному из материала №7 таблицы 2.1(латунь), диаметр d сечения проводника равен 1,51 мм,. Определить сpeднюю скорость <υ>направленного движения электронов, считая, что концентрация n свободных электронов равна концентрации п' атомов проводника.

Характеристики материалов

Таблица 2.1

№	Металл или сплав	Плотность, 103 кг/м3	Молярная масса, 10-3 кг/моль
7	Латунь	8,6	67,3

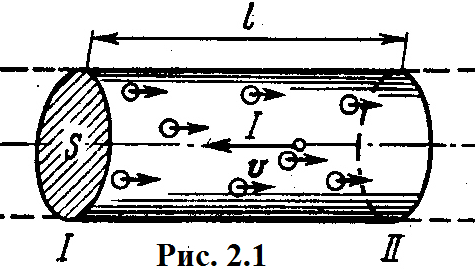Р ешение

Средняя скорость направленного (упорядоченного) движения электронов определяется по формуле

<υ>=l/t, (1)

где t- время, в течение которого все свободные электроны, находящиеся в отрезке проводника между сечениями I и II, пройдя через сечение II (рис. 2.1), перенесут заряд Q=eN и создадут –ток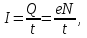

(2)

где е = 1,6*10^-19К - элементарный заряд; N- число электронов в отрезке проводника.

Число свободных электронов в отрезке проводника объёмом Vможно выразить следующим образом:

N=nV=nlS, (3)

где S - площадь сечения.

По условию задачи, п=п'. Следовательно,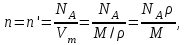

(4)

где N_A = 6,02*10²³ к моль^-1 - постоянная Авогадро; V_m - молярный объём латуни; М = 67.3 - молярная масса латуни из таблицы 2; ρ - его плотность. Для железа ρ = 8.6*10³ кг/м³.

Подставив последовательно выражения п из формулы (4) в равенство (3) и N из формулы (3) в равенство (2), получим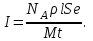



Отсюда найдём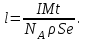



Подставив выражение lв формулу (1), сократив на t и выразив площадь S сечения проводника через диаметр d, найдём среднюю скорость направленного движения электронов: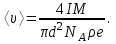

(5)

Произведём вычисления по этой формуле: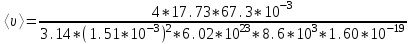



<υ>=0.000805 м/с=0,805 мм/с.

Задача 2.2

В цепь источника постоянного тока с ЭДС ε=6,56В включён резистор сопротивлением R=84,2Ом. Определить:

1) плотность тока в соединительных проводах площадью поперечного сечения S=2,89мм²;

2) число N электронов, проходящих через сечение проводов за время t= 1,52 с. Сопротивлением источника тока и соединительных проводов пренебречь.

Решение

1. Плотность тока по определению есть отношение силы тока I к площади поперечного сечения провода:

j=I/S. (1)

Силу тока в этой формуле выразим по закону Ома: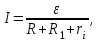

(2)

где R - сопротивление резистора; R₁- сопротивление соединительных проводов; r_i- внутреннее сопротивление источника тока.

Пренебрегая сопротивлениями R_lи r_iиз (2), получим

I =ε/R.

Подставив это выражение силы тока в (1), найдём

j =ε/(RS)

j =6.56/(84.2*2.89)

Произведя вычисления по этой формуле, получим

j=2.69*10⁴ A/м

2. Число электронов, проходящих за время t через поперечное сечение, найдём, разделив заряд Q, протекающий за это время через сечение, на элементарный заряд

N =Q/e,

или с учётом того, что Q=It и I=ε/R, получим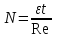



Подставим сюда числовые значения величин и вычислим (элементарный заряд: e=1,60*10^-19 Кл):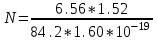



N =7.40*10¹⁷ электронов.

Задача 2.3

Пространство между пластинами плоского конденсатора имеет объём V=392 см³ и заполнено водородом, который частично ионизирован. Площадь пластин конденсатора S=255 см². При каком напряжении U между пластинами конденсатора сила тока I, протекающего через конденсатор, достигнет значения 2.7 мкА, если концентрация n ионов обоих знаков в газе равна 5,86*10⁷ см^-3. Принять подвижность ионов b₊=5,4*10^-4м²/(В*с), b_–=7,4*10^-4 м²/ (В*с) ; e (Q)=1,60*10^-19 Кл.

Решение

Напряжение U на пластинах конденсатора связано с напряжённостью Е электрического поля между пластинами и расстоянием d между ними соотношением

U=Ed. (1)

Напряжённость поля может быть найдена из выражения плотности тока

j=Qn(b₊+b_-)E,

где Q - заряд иона. Отсюда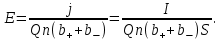



Расстояние dмежду пластинами, входящее в формулу (1), найдём из соотношения

d=V/S.

Подставив выражения Е и dв (1), получим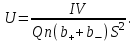

(2)

Проверим, дает ли правая часть полученной расчётной формулы единицу напряжения: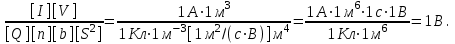



Подставим в формулу (2) значения величин и произведём вычисления: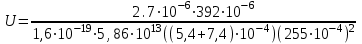



U=135.62 B.