Прикладная физика в электроэнергетике. ЭПбз-18-2 49 Маризов А.А.. Иркутский национальный исследовательский
 Скачать 1.38 Mb. Скачать 1.38 Mb.
|
|
Задача 4.3 На проволочный виток радиусом г=11,6см, помещенный между полюсами магнита, действует максимальный механический момент Мmax=6,7 мкН. Сила тока I в витке равна 37,3А. Определить магнитную индукцию Вполя между полюсами магнита. Действием магнитного поля Земли пренебречь. Решение. Индукцию Вмагнитного поля можно определить из выражения механического момента, действующего на виток с током в магнитном поле, Если учесть, что максимальное значение механический момент принимает при α=π/2(sin α=l), а также что pm=IS, то формула (1) примет вид Отсюда, учитывая, что S=πr2, находим 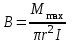 (2) (2)Произведя вычисления по формуле (2), найдём 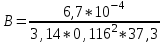 В=4.25*10-6 Тл. Закон полного тока. Магнитный поток. Магнитные цепи Связь между магнитной индукцией В поля в ферромагнетике и напряжённостью Н намагничивающего поля выражается графически 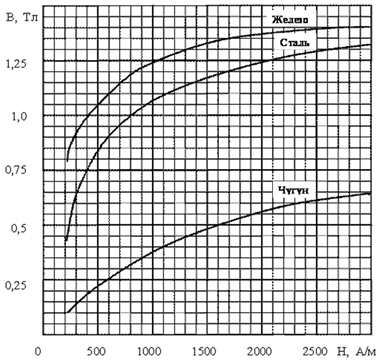 Рис. 5.1 Задача 5.1 В одной плоскости с бесконечно длинным прямым проводом, по которому течёт токI=53,6 А, расположена прямоугольная рамка так, что две большие стороны ее длиной l=70,5 см параллельны проводу, а расстояние от провода до ближайшей из этих сторон равно ее ширине. Каков магнитный поток Ф, пронизывающий рамку? Р 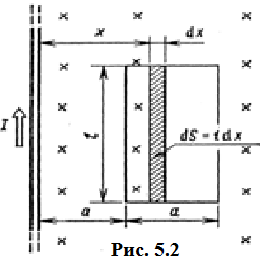 ешение ешениеМагнитный поток Ф через поверхность площадью S определяется выражением 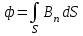 В нашем случае вектор магнитной индукции В перпендикулярен плоскости рамки. Поэтому для всех точек рамки Вn=В. Магнитная индукция В, создаваемая бесконечно длинным прямым проводником с током, определяется формулой 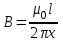 , ,где x— расстояние от провода до точки, в которой определяется В. Для вычисления магнитного потока заметим, что так как В зависит от х и элементарный поток Ф будет также зависеть от х, то dф=B(x)dS. Разобьём площадь рамки на узкие элементарные площадки длиной l, шириной dx и площадью dS=ldx (рис. 5.2). В пределах этой площадки магнитную индукцию можно считать постоянной, так как все части площадки равноудалены (на расстояние х) от провода. С учётом сделанных замечаний элементарный магнитный поток можно записать в виде dФ= 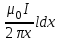 Проинтегрировав полученное выражение в пределах от x1=a до х2=2а, найдём 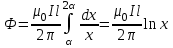 |2. |2. Подставив пределы, получим 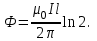 (1) (1)Убедимся в том, что правая часть полученного равенства дает единицу магнитного потока (Вб): [0] [I] [l]= Гн/м 1 А 1 м=1 Вб. Произведя вычисления по формуле (1), найдём 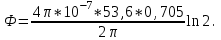 Ф=5,28*10-8 Вб. Задача 5.2 Определить индукцию В и напряжённость Н магнитного поля на оси тороида без сердечника, по обмотке которого, содержащей N=202 витков, идет ток I=5,06 А. Внешний диаметр d1тороида равен 32,3 см, внутренний d2= 20,6 см. Решение. Для определения напряжённости магнитного поля внутри тороида вычислим циркуляцию вектора Н вдоль линии магнитной индукции поля: 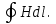 Из условия симметрии следует, что линии магнитной индукции тороида представляют собой окружности и напряжённости во всех точках этой линии одинаковы. Поэтому в выражении циркуляции напряжённость Н можно вынести за знак интеграла, а интегрирование проводить в пределах от нуля до 2 r, где r — радиус окружности, совпадающей с линией индукции, вдоль которой вычисляется циркуляция, т. e. 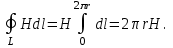 (1) (1)С другой стороны, в соответствии с законом полного тока циркуляция вектора напряжённости магнитного поля равна сумме токов, охватываемых контуром, вдоль которого вычисляется циркуляция: 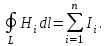 (2) (2)Приравняв правые части равенств (1) и (2), получим 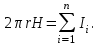 (3) (3)Линия, проходящая вдоль тороида, охватывает число токов, равное числу витков тороида. Сила тока во всех витках одинакова. Поэтому формула (3) примет вид 2rH=-NI, откуда 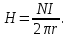 (4) (4)Для средней линии тороида r=1/2(R1R2)=1/4(d1+d2). Подставив это выражение r в формулу (4), найдём 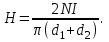 (5) (5)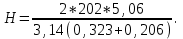 H=1,23 кА/м Магнитная индукция В0в вакууме связана с напряжённостью поля соотношением B0=0H. Следовательно, 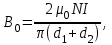 (6) (6)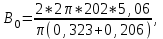 B0=1,54*10-3 Тл Подставив значения величин в выражения (5) и (6), получим: B0=1,54*10-3 Тл. Пример. 5.3 Чугунное кольцо имеет воздушный зазор длиной lо=5,92 мм. Длина l средней линии кольца равна 1,44 м. Сколько витков N содержит обмотка на кольце, если при силе тока I=4,04 А индукция В магнитного поля в воздушном зазоре равна 0,625 Тл? Рассеянием магнитного потока в воздушном зазоре можно пренебречь. Явление гистерезиса не учитывать. Решение Пренебрегая рассеянием магнитного потока, мы можем принять, что индукция поля в воздушном зазоре равна индукции поля в чугуне. На основании закона полного тока запишем IN=Hl+H0I0. 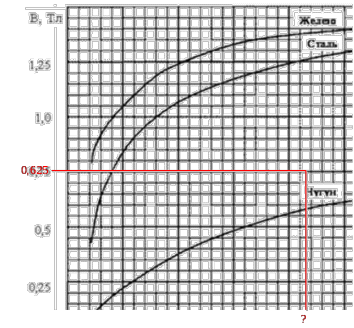 По графику (см. рис. 5.1) находим, что при В=0,625 Тл напряжённость Н магнитного поля в чугуне равна 2600 А/м. Так как для воздуха =1, то напряжённость поля в воздушном зазоре при 0 =4 10-7 равна По графику (см. рис. 5.1) находим, что при В=0,625 Тл напряжённость Н магнитного поля в чугуне равна 2600 А/м. Так как для воздуха =1, то напряжённость поля в воздушном зазоре при 0 =4 10-7 равна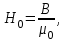 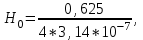 H0 =49,76 кА/м. Искомое число витков 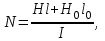 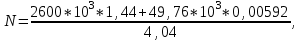 N=1655,90 т.е. 1655 витков. Работа по перемещению проводника с током в магнитном поле. Электромагнитная индукция. Индуктивность Задача 6.1 Виток, по которому течёт ток I=22,6 А, свободно установится в однородном магнитном поле В=18,5 мТл. Диаметр d витка равен 10,2 см. Какую работу нужно совершать, чтобы медленно повернуть виток на угол =/2 относительно оси, совпадающей с диаметром? Р 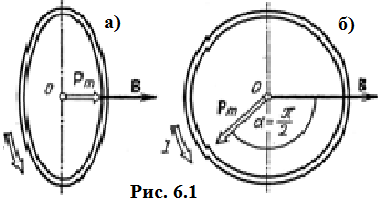 ешение ешениеПри медленном повороте контура в магнитном поле индукционными токами можно пренебречь и считать ток в контуре неизменным. Работа сил поля в этом случае определяется выражением где Ф1 и Ф2 – магнитные потоки, пронизывающие контур в начальном и конечном положениях. Работа внешних сил будет равна модулю работе сил поля и противоположна ей по знаку, т. е. Так как в начальном положении контур установился свободно (положение устойчивого равновесия), то момент внешних сил, действующий на контур, равен нулю. В этом положении вектор магнитного момента pm контура сонаправлен с вектором В (рис. 6.1, а) и магнитный поток Ф1 максимален (=0, cos =1), т. е. Ф1=ВS (где S – площадь контура). В конечном положении (рис. 6.1, б) вектор pm перпендикулярен вектору B (=/2, cos =0) и магнитный поток Ф2=0. Перепишем выражение (1) с учётом сделанных замечаний: Так как площадь контура S=d2/4. то работа Убедимся в том, что правая часть равенства дает единицу работы (Дж): Произведём вычисления: 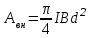 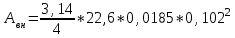 Авн = 3,415*10-3 Дж. Задача 6.2 В однородном магнитном поле с индукцией B=0,25 Тл равномерно вращается рамка, содержащая N= 1064 витков, с частотой n=10,4 c -1. Площадь S рамки равна 154 см2. Определить мгновенное значение ЭДС 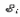 , соответствующее углу поворота рамки 60°. , соответствующее углу поворота рамки 60°.Решение Мгновенное значение ЭДС индукции 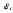 , определяется основным уравнением электромагнитной индукции Ленца: , определяется основным уравнением электромагнитной индукции Ленца:Потокосцепление =NФ, где N — число витков, пронизываемых магнитным потоком Ф. Подставив выражение в формулу (1), получим При вращении рамки магнитный поток Ф, пронизывающий рамку в момент времени t, изменяется по закону Ф=ВS cos t, где В — магнитная индукция; S – площадь рамки; – угловая частота. Подставив в формулу (2) выражение Ф и продифференцировав по времени, найдём мгновенное значение ЭДС индукции: Угловая частота со связана с частотой п вращения соотношением =2п. Подставив выражение со в формулу (3) и заменив t на угол , получим Убедимся в том, что правая часть полученного равенства дает единицу ЭДС (В). Учтя, что 2 , N и sin t — величины безразмерные и неименованные, получим Произведя вычисления по формуле (4), найдём 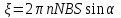 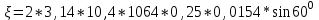 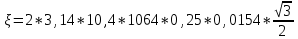 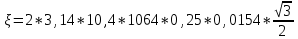 ξi = 231,69 B. Задача 6.3 По соленоиду течёт ток I=2,18 А. Магнитный поток Ф, пронизывающий поперечное сечение соленоида, равен 6,65 мкВб. Определить индуктивность L соленоида, если он имеет N=828 витков. Решение Индуктивность L соленоида связана с потокосцеплением соотношением =LI, откуда L=/I. Заменив здесь потокосцепление его выражением через магнитный поток Ф и число витков N соленоида (=ФN), получим 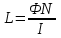 (1) (1)Произведя вычисления по формуле (1), получим 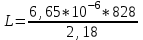 L = 2,52*10-3 Гн. Энергия магнитного поля Задача 7.1 На стержень из немагнитного материала длиной l=50,8 см намотан в один слой провод так, что на каждый сантиметр длины стержня приходится n = 27 витков. Определить энергию W магнитного поля внутри соленоида, если сила тока I в обмотке равна 1,01 А. Площадь S сечения стержня равна 3,45 см2. Решение Энергия магнитного поля соленоида с индуктивностью L, по обмотке которого течёт ток I, выражается формулой 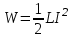 . (1) . (1)Индуктивность соленоида в случае немагнитного сердечника зависит только от числа витков на единицу длины и от объёма V сердечника: L=μ0n2V, где μ0 –магнитная постоянная. Подставив выражение индуктивности L в формулу (1), получим 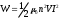 . Учтя, что V=lS, запишем . Учтя, что V=lS, запишем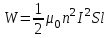 . (2) . (2)Сделав вычисления по формуле (2), найдём 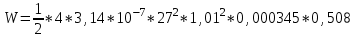 W=8,18*10-8 Дж. Задача 7.2 По обмотке метрового соленоида со стальным сердечником течёт ток I=1.41 А. Определить объёмную плотность W энергии магнитного поля в сердечнике, если число п витков на каждом сантиметре длиныl соленоида равно 9 см-1. Решение Объёмная плотность энергии магнитного поля определяется по формуле 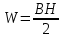 (1) (1)Напряжённость Н магнитного поля найдём по формуле H=nlI. По закону полного тока 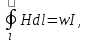 где 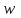 - число витков, равное - число витков, равное 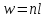 . .Так как взятие интеграла 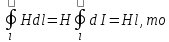 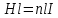 Отсюда 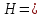 Подставив сюда значения п, lнайдёмколичество витков соленоида (п =9 см-1 или n=9/0,01 м-1) и I, найдём 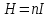 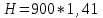 H=1269 А/м Магнитную индукцию В определим по графику (см. рис. 5.1) зависимости В от Н.  Рис. 5.1 Находим, что напряжённости H=1269 А/м соответствует магнитная индукция B=1,12 Тл. Произведя вычисление по формуле (1), найдём объёмную плотность энергии: 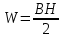 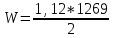 W=710,64 Дж/м3. Задача 7.3 На железный сердечник длиной l=11 см малого сечения (d<l) намотано N=138 витков. Определить магнитную проницаемость μ железа при силе тока I=0,579 А. Решение Магнитная проницаемость μ связана с магнитной индукцией В и напряжённостью Н магнитного поля соотношением B= μ0μH. (1) Эта формула не выражает линейной зависимости В от Н, так как μ является функцией Н. Поэтому для определения магнитной проницаемости обычно пользуются графиком зависимости В(Н) (см. рис. 5.1). Из формулы (1) выразим магнитную проницаемость: 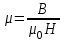 (2) (2)Напряжённость Н магнитного поля вычислим по формуле (катушку с малым сечением можно принять за соленоид) Н=п1, где п — число витков, приходящихся на отрезок катушки длиной 1 м. Выразив в этой формуле п через число N витков катушки и ее длину l, получим 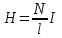 Подставив сюда значения N, l и I и произведя вычисления, найдём 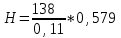 H=726,38 А/м. По графику Рис. 5.1 находим, что для железа напряжённости Н=726,38 А/м соответствует магнитная индукция B=1,16 Тл. Подставив найденные значения В и Н, а также значение 0 =4*10-7 в формулу (2), вычислим магнитную проницаемость: 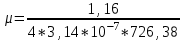 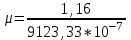 μ=1274,72 |
