Прикладная физика в электроэнергетике. ЭПбз-18-2 49 Маризов А.А.. Иркутский национальный исследовательский

• Название: Иркутский национальный исследовательский
• Анкор: Прикладная физика в электроэнергетике
• Дата: 13.03.2022
• Размер: 1.38 Mb.
• Имя файла: ЭПбз-18-2 49 Маризов А.А..docx
• Тип: Документы; #394100
• страница: 2 из 3

Магнитное поле постоянного тока

Задача 3.1

Два параллельных бесконечно длинных провода, по которым текут в одном направлении токи I=61,8 А, расположены в точках D и С. Расстояние между проводами d=12,5см. Определить магнитную индукцию В в точке А, отстоящей от одного проводника на расстоянии г₁=5,34 см и от другого – на расстоянии r₂=16см.

Р 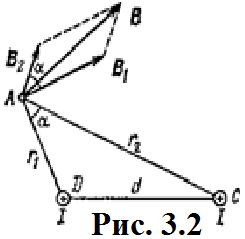ешение

Для нахождения магнитной индукции в указанной точке А (рис. 3.2) определим направления векторов индукций В₁ и В₂ полей, создаваемых каждым проводником в отдельности, и сложим их геометрически, т. е. B=B₁+B₂. Модуль индукции найдём по теореме косинусов: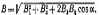

(1)

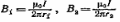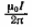Значения индукций Biи В₂ выражаются соответственно через силу тока I и расстояния r₁ и r₂ от провода до точки, индукцию в которой мы вычисляем: , где ₀ =4 10 ^-7 Гн/м. Подставляя B₁и В₂в формулу (1) и вынося за знак корня, получим

(2)

Убедимся в том, что правая часть этого равенства даёт единицу магнитной индукции (Тл):



Откуда следует, что



Вычисляем cos. Заметим, что =∠DAC. Поэтому по теореме косинусов запишем 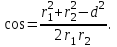, где d– расстояние между проводами. Отсюда



Подставив данные, вычислим значение косинуса: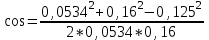



cos = 0,750.

Подставив в формулу (2) значения ₀ =4 10 ^-7 Гн/м, I, r₁, r₂и cos α, найдём B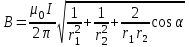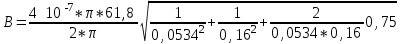





В=2960,23*10^-7 Тл.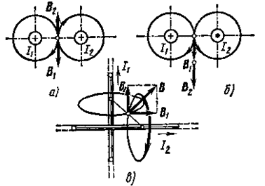




Рис 3.3
Задача 3.2

По двум длинным прямолинейным проводам, находящимся на расстоянии r=6,03 см друг от друга в воздухе, текут токи I₁=11.74 А, I₂=17.86 А. Определить магнитную индукцию Вполя, создаваемого токами в точке а=0,63rот левого провода для случаев:

1-й случай: провода параллельны, токи текут в одном направлении (рис. 3.3, а);

2-й случай: провода параллельны, токи текут в противоположных направлениях (рис. 3.3, б);

3-й случай: провода перпендикулярны, направление токов указано на рис. 3.3, в, в этом случае точка а лежит на диагонали квадрата со стороной r на расстоянии а=0,63rот вертикального провода.

Решение

Результирующаяиндукция магнитного поля равна векторной сумме: B=B₁+B₂, где B₁ – индукция поля, создаваемого током I₁;В₂ – индукция поля создаваемого током I₂.

Если B₁ и В₂ направлены по одной прямой, то векторная сумма может быть заменена алгебраической суммой:

В=В₁+В₂. (1)

При этом слагаемые В₁и В₂должны быть взяты с соответствующими знаками. Вычислим эти индукции по формуле

B₁=₀I₁/(2ar), B₂=₀I₂/(2(1-a)r), (2)

где ₀ =4 10 ^-7 Гн/м.

Подставив значения величин в формулs (2), найдём модули В₁ и В₂: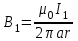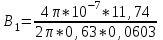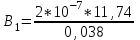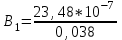

;

;





В₁=617,89*10^-7 Тл,

В₁=0,61*10^-4 Тл.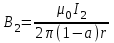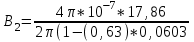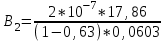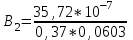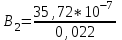



;







В₂=1623,63*10^-7 Тл,

В₂=1,62*10^-4 Тл.

1-й случай: Векторы B₁ и В₂ направлены по одной прямой (рис. 3.3, а); следовательно, результирующая индукция В определяется по формуле (1). Приняв направление вверх положительным, вниз – отрицательным, запишем: В₁=0,61*10^-4 Тл. , В₂=1,62*10^-4 Тл.

Подставив в формулу (1) эти значения В₁и B₂, получим

В=В₁+В₂

B= - 0,61*10^-4 +1,62*10^-4

В = 1,01*10^-4 Тл

2-й случай: Векторы В₁ и В₂ направлены по одной прямой в одну сторону (рис. 3.3, б) и их значения отрицательны..

Подставив в формулу (1) значения B₁ и В₂ получим

В= - В₁ - В₂

B= - 0,61*10^-4 -1,62*10^-4

В = - 2,23*10^-4 Тл

3-й случай. Векторы индукций магнитных полей, создаваемых токами в точке а=0,63rот вертикального провода взаимно перпендикулярны (рис. 3.3, в). Результирующая индукция по модулю и направлению является диагональю прямоугольника, построенного на векторах В₁ и В₂, создаваемые токами I₁, I₂, соответственно. Вектор В₁=₀I₁/(2ar). Подставив значения, получим В₁=617,89*10^-7. Если подумать, то для индукции В₂ справедлива формула (2), то есть В₂=1623,63*10^-7 Тл.

По теореме Пифагора найдём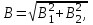

(3)

Подставив в формулу (3) значения В₁и В₂и вычислив, получим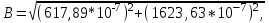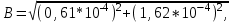





B=1,72*10^-4 Тл.

Задача 3.3

Определить магнитную индукцию В поля, создаваемого отрезком бесконечно длинного прямого провода, в точке, равноудалённой от концов отрезка и находящейся на расстоянии r₀=21.5 см от середины его (рис. 3.4). Сила тока I, текущего по проводу, равна 32.9 А, длина l отрезка равна 65.4 см.

Р 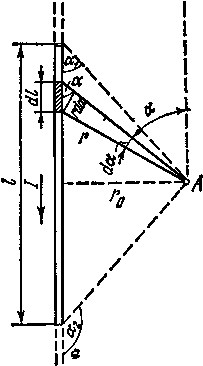ешение

Для определения магнитной индукции поля, создаваемого отрезком провода, воспользуемся законом Био –Савара–Лапласа:



(1)

П режде чем интегрировать выражение (1), преобразуем его так, чтобы можно было интегрировать по углу . Выразим длину элемента dl проводника через d. Согласно рис. 3,4 запишем

Рис. 3.4

Подставим это выражение dl в формулу (1):



Но r – величина переменная, зависящая от  и равная 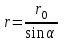Подставив rв предыдущую формулу, найдём

(2)

Чтобы определить магнитную индукцию поля, создаваемого отрезком проводника, проинтегрируем выражение (2) в пределах от ₁ до ₂: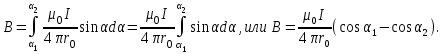

(3) Заметим, что при симметричном расположении точки A относительно отрезка провода cos ₂= – cos ₁. С учётом этого формула (3) примет вид

(4)

Из рис. 3.4 следует



Подставив выражение cos ₁ в формулу (4), получим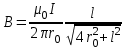

(5)

Подставим числовые значения в формулу (5) и произведём вычисления: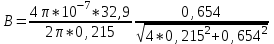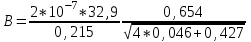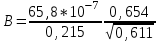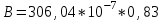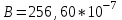











B=256,60*10^-7 Тл.

Силы, действующие на движущиеся заряды в магнитном поле

Задача 4.1

По двум параллельным прямым проводам длиной l=3,33 м каждый, находящимся на расстоянии d=22,4см друг от друга, текут одинаковые токи I=1,75 кА. Вычислить силу Fвзаимодействия токов.

Р 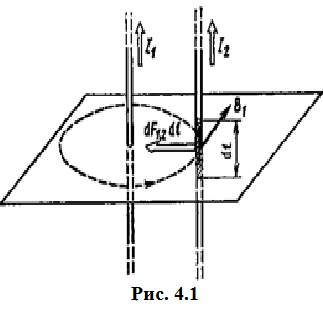ешение

Взаимодействие двух проводников, по которым текут токи, осуществляется через магнитное поле. Каждый ток создает магнитное поле, которое действует на другой проводник. Предположим, что оба тока (обозначим их 1_ги I₂) текут в одном направлении.

Вычислим силу F₁,₂, с которой магнитное поле, созданное током I₁, действует на проводник с током I₂. Для этого проведём магнитную силовую линию так (штриховая линия на рис. 4.1), чтобы она касалась проводника с током I₂. По касательной к силовой линии проведём вектор магнитной индукции В₁. Модуль магнитной индукции B₁ определяется соотношением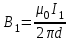

(1)

Согласно закону Ампера, на каждый элемент второго проводника с током I₂ длиной dl₂ действует в магнитном поле сила (длинный проводник (l>>d) можно приближенно рассматривать как бесконечно длинный)



Так как отрезок dl перпендикулярен вектору B₁, то и тогда

⁽²⁾

Подставив в выражение (2) В₁из (1), получим



Силу F_1,2 взаимодействия (по третьему закону Ньютона, сила, действующая на первый проводник со стороны второго, будет равна найденной по модулю и противоположной по направлению) проводников с током найдём интегрированием по всей длине второго проводника;



Заметив, что I₁=I₂=I и l₂=l, получим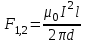

Убедимся в том, что правая часть этого равенства дает единицу силы



Произведём вычисления: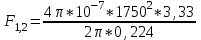



F_1,2=9,10 H.

Сила F₁,₂ сонаправлена с силой dF₁,₂ (рис. 4.1) и определяется (в данном случае это проще) правилом левой руки.

Задача 4.2

Провод в виде тонкого полукольца радиусом R=11.3 см находится в однородном магнитном поле B=53.5 мТл. По проводу течёт ток I=11.9 А. Найти силу F, действующую на провод, если плоскость полукольца перпендикулярна линиям магнитной индукции, а подводящие провода находятся вне поля.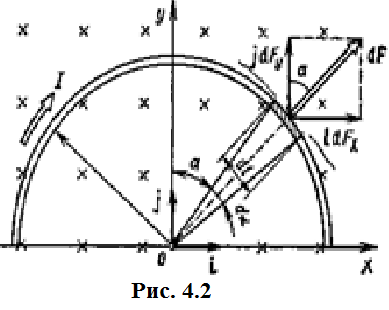

Решение

Расположим провод в плоскости чертежа перпендикулярно линиям магнитной индукции (рис. 4.2) и выделим на нем малый элемент dl с током. На этот элемент тока Idlбудет действовать по закону Ампера сила dF=I[dlB]. Направление этой силы можно определить по правилу векторного произведения или по правилу левой руки.

Используя симметрию, выберем координатные оси так, как это изображено на рис. 4.2. Силу dF представим в виде



где i и j – единичные векторы (орты); dF_xи dF_y — проекции вектора dF на координатные оси Ох и Оу.

Силу F, действующую на весь провод, найдём интегрированием:



где символ Lуказывает на то, что интегрирование ведется по всей длине провода L. Из соображений симметрии первый интеграл равен нулю 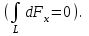тогда

⁽¹⁾

Из рис. 4.2 следует, что

^{где dF – модуль вектора Вектор dl перпендикулярен вектору то Выразив длину дуги dl через радиус Rи угол α, получим}



Тогда

Введём dF_yпод интеграл соотношения (1) и проинтегрируем в пределах от -π/2 до +π/2 (как это следует из рис. 4.2):



Из полученного выражения видно, что сила F сонаправлена с положительным направлением оси Оу (единичным вектором j).

Найдём модуль силы F:



Убедимся в том, что правая часть этого равенства дает единицу силы  (Н):



Произведём вычисления: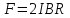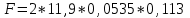





F=0,14 H.