Испытания на надежность. Испытания на надежность Значение и виды испытаний на надежность
 Скачать 287.95 Kb. Скачать 287.95 Kb.
|
|
Испытания на надежность Значение и виды испытаний на надежность Испытания на надежность – обязательный вид испытаний. Общая их цель – установить, какой надежностью обладают изделия в условиях, предписываемых методикой испытаний. Испытания на надежность проводятся как комплекс мероприятий по определению показателей надежности на этапах производства и проектирования, а также с целью контроля надежности разрабатываемых и выпускаемых РЭС (ЭВС). Объектом испытаний является партия изделий, из которой берется выборка (sample). С испытаниями на надежность связаны некоторые проблемы. Во-первых, эти испытания требуют больших затрат времени и средств; во-вторых, в процессе их проведения расходуется часть ресурса изделий; в третьих, есть проблема доверия результатам испытаний. Испытания (И) на надежность, в зависимости от цели проведения, подразделяют на определительные и контрольные. Определительные И на надежность проводятся для установления показателей надежности изделий. Эти показатели (прежде всего, среднее время наработки до отказа, вероятность безотказной работы за назначенное время, интенсивность отказов, средняя наработка на отказ) включают затем в нормативно-техническую документацию на изделие. Большое значение при проведении определительных И имеет верный выбор параметров, информирующих о состоянии изделия (работает или отказывает). Контрольные И на надежность проводятся для контроля соответствия или несоответствия партии изделий заданному уровню надежности. По результатам этих И объект испытаний (партию изделий) относят – с заданным риском - либо к категории годных либо негодных по уровню их надежности. Используют и специальные виды испытаний на надежность, такие как: испытания на срок службы; ускоренные испытания на срок службы; испытания на (не)разрушающие под влиянием определенных факторов. При ускоренных испытаниях все в принципе делается как и при неускоренных испытаниях, но при повышенных нагрузках (электрических, тепловых и др.) При испытаниях на разрушение нагрузку увеличивают до тех пор, пока это не вызовет отказ изделия. Испытания классифицируют и еще по ряду признаков: стадии создания или эксплуатации объектов; месту и условиям проведения (лабораторные, испытания в условиях эксплуатации…); по используемым методам и аппаратуре (моделирование, натурный эксперимент); по уровню объектов (комплектующих элементов, отдельных устройств, систем). Результаты определительных И представляются в виде: статистики отказов испытываемых объектов; множества значений выходных параметров объектов; характеристик наблюдаемых изменений физико-химических процессов в материалах объектов. Определительные испытания на надежность Данные испытания, цель которых – определение показателей надежности – могут проводиться по различным планам. План испытаний (И) включает: число (N) устанавливаемых на И объектов; указание на число заменяемых или воостанавливаемых объектов в процессе И (U – объекты не восстанавливаются и не заменяются; R – заменяемых в случае отказа объектов; M – число восстанавливаемых объектов); число отказов r, до накоплении которых И продолжают; заданное время T проведения И; Так план [NUT] предписывает проведение И в течение времени Т N объектов без их замены / восстановления. План [NUr] отличается от предыдущего тем, что И проводят до накопления r отказов. Наиболее полную информацию дает план [NUN], в соответствии с которым N объектов (изделий) испытывают без их замены / восстановления до отказа каждого из них. Здесь раскрывается вся эмпирическая картина распределения отказов во времени. Задача нахождения показателей надежности наиболее точно и полно решается при знании закона распределения времени работы изделий до отказа. Предположим, что имеется множество результатов наблюдений над непрерывной случайной величиной (СВ), каковой при испытаниях на надежность является время отказа одного из множества изделий в испытываемой партии. Закон распределения этой СВ в первом приближении может быть установлен по статистическому ряду, построенному на основе собранного экспериментального материала. Выбор и проверка гипотезы о законе распределения . Построенная на основании статистического ряда гистограммадает возможность выдвинуть гипотезу о законе распределения и затем оценить степень согласованности теоретического и статистического распределений. Построение гистограммы 1. По исправленным результатам испытаний, т.е. по реальным результатам (с вычетом систематической погрешности) строится вариационный ряд – упорядоченная выборка. Результаты в таком ряду располагают в порядке возрастания их числовых значений. Применительно к задаче обработки статистики времени безотказной работы объектов вариационный ряд выстраивается естественным образом – в порядке появления отказов. 2. Этот ряд разбивается на некоторое число Nинтервалов группирования экспериментальных результатов, причем интервалов одинаковой ширины.h. ЧислоNдолжно быть оптимально в смысле достаточной выразительности и защищенности от незакономерных колебаний. 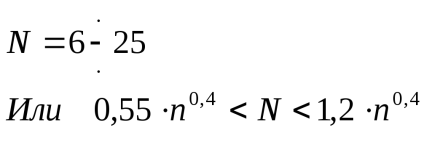 При числе результатов измерений (числе отказов) n≈ 150 3. Подсчитывают количество значений mk результатов, приходящихся на каждыйk-тый интервал (разряд) т. е. определяют абсолютные частости 4. Строится гистограмма. По оси результатов откладываются интервалы значений наблюдаемой СВ, по оси ординат – частости. На каждом основании шириной hстроится прямоугольник высотой   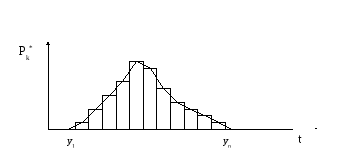 Рис. 1 Ординаты, пропорциональные частям, восстановленные в серединах столбцов перпендикулярно оси абсцисс, позволяют построить полигон (рис. 1). Сопоставление полученного на основе набранной статистики полигона с различными кривыми плотностей распределения позволяет выдвинуть гипотезу о законе распределения. Далее необходимо оценить, насколько с этой гипотезой согласуются экспериментальные данные. 5. При числе наблюдений больше 50 для проверки правдоподобия выдвинутой гипотезы о законе распределения используется критерий Пирсона (наиболее применяемый критерий согласия). Для этого надо располагать статистическим рядом: Для гипотетического распределения находят теоретические вероятности: В качестве меры расхождения между теоретической вероятностью и найденной из опытов статистической вероятностью выбирается мера Здесь Введенная мера χ2 – СВ, имеющая распределение Пирсона с числом степеней свободыr = N – 1 – ν, гдеν – число параметров, однозначно определяющих данный закон распределения. Составлены таблицы значений χ2 для различных уровней значимостиq = 1 – Pдов, где Pдов – доверительная вероятность, с которой гипотеза о законе распределения принимается(табл – в прилож?). Если вычисленная по экспериментальным данным мера мераχ2 < (χ2)q то с вероятностьюq гипотеза о законе распределения принимается. В настоящее время для проверки гипотеы принята двусторонняя критическая область, то есть гипотеза принимается, если χ2r,(1-q/2) < χ2 < χ2r; q/2 (6.2) При знании закона распределения показатели надежности могут быть вычислены на основе достаточно ограниченного набора экспериментальных данных. Это иллюстрируется следующим примером. Пример. За время испытаний 100 изделий в течение tи = 200 ч зафиксированы отказы 2-х изделий. Определить среднее время Т1 наработки до отказа, если известно, что случайное время отказа изделия подчинено экспоненциальному закону. Вероятность отказа рассчитывается по формуле Согласно результатам И статистическое значение Q равно 0,02. Таким образом, где t = tи = 200 ч. Получаем Если в результате проведенных И получен ряд значений ti(случайных значений времени отказа), точечные оценки мат. ожидания и дисперсии среднего времени наработки до отказа Т1находятся по формулам: Любая точечная оценка, полученная на основании испытаний, обладает тем существенным недостатком, что она сама является случайной величиной. Поэтому для точечных оценок необходимо находить доверительные интервалы, в которые они попадают с доверительной вероятностью β. Показательным в этом плане является нахождение доверительного интервала для средней наработки на отказ. Рассмотрим простейший пуассоновский поток отказов РЭС (ЭВС). Вероятность появления k отказов за время tΣ в соответствии с законом Пуассона будет где λ = 1/To. Вероятность работы с числом отказов ≤ r рассчитывается, согласно (6) как Выражение (7) соответствует интегральной функции χ2-распределения случайной величины tΣ до появления r отказов. Собственно χ2-распределению с ν = 2r степенями свободы подчинена случайная величина Дифференцирование этой функции по dχ2 дает функцию плотности распределения (рис. ). В качестве доверительного интервала при заданной доверительной вероятности β принимается двусторонняя критическая область χ2ν,(1-q/2) < χ2 < χ2ν; q/2 , (9) Тогда величина ТОнаходится в доверительном интервале Значения меры χ2 в завсисмости от уровня значимости q и числа степеней свободы ν даны в таблице № Табл. №
Пример. Пусть за суммарное времяtΣ= 5000 ч испытаний однотипных РЭС произошлоr = 14 отказов. Оценить с доверительной вероятностьюβ= 0,9 граничные значения среденей наработки на отказ. Среднее время наработки на один отказ равно Величина TO случайная. Поэтому необходимо определить доверительный интервал, в котором величинвТО находится с доверительной вероятностью β. Согласно исходным данным 2tΣ= 10000 ч,ν = 2r= 28,q/2 = (1-β)/2 = 0,05. По табл.№находим Таким образом, согласно (6.10), величина ТОнаходится в пределах 242 ч < ТО < 590 ч. Контрольные испытания на надежность Задача контрольных испытаний: установить соответствие (или несоответствие) надежности партии изделий заданному уровню по результатам испытаний выборки. При планировании этих испытаний задают: время испытаний tи; объем выборки n; приемочное число С (максимальное допустимое число отказавших за время испытаний изделий, при котором партия принимается); риск заказчика β и (в общем случае) риск изготовителя α. Контрольные испытания проводят одним из следующих методов: однократной выборки; последовательных испытаний (что является развитием метода однократной выборки); двукратной выборки. Каждый из этих методов, являясь по сути выборочным, позволяет судить о характеристике всей генеральной совокупности N изделий на основании испытаний извлеченной путем случайного отбора из этой совокупности выборки объемом n < N. Эта особенность контрольных испытаний предопределяетследующиериски: 1) забраковать по результатам испытаний годную партию с вероятностью α (риск изготовителя-поставщика); 2) принять с вероятностью β (риск заказчика) партию изделий, не отвечающих по по уровню надежности заданным требованиям.  Рис.2 Зависимость вероятности приемки партии p по результатам выборочного контроля от числа дефектных изделий в партии Предположим, что в партии объемом N изделий D из них не выдержат испытаний в течение заданного времени tи и откажут. При уровне дефектности Q = D/N вероятность p приемки партии по выборке будет зависеть от установленных значений приемочного и браковочного уровней дефектности (соответственно Q/ и Q//). Если задана вероятность P(t) безотказной работы за tи, соответствующий ей уровень дефектности определяется как Q = 1 – P(t). (6.12) При контроле по браковочному (гарантированному) уровню дефектности Q// (с соответствующей браковочной вероятностью P2 = 1 - Q//) заказчику с вероятностью β гарантируется надежность изделий не ниже P2 . Приемочный уровень дефектности Q/ = 1 – P1оставляет вероятность α браковки партии по результатам испытаний выборки. При планировании контрольных испытаний учитывают либо только интересы заказчика (планирование по браковочному уровню дефектности) либо интересы и заказчика и поставщика (планирование по браковочному и приемочному уровням дефектности). Рассмотрим более подробно планирование контрольных испытаний. Метод однократной выборки. Сначала рассмотрим планирование по браковочному (гарантированному) значению вероятности безотказной работы. Этот метод применим как при известном, так и при неизвестном законе распределения контролируемого показателя надежности. При рассматриваемом методе испытаний партия принимается как соответствующая заданному уровню надежности, если в выборке объемом n из этой партии дефектных изделий окажется d ≤ C, где С – приемочное число. Для выборки n < 0,1 N и высокой вероятности безотказной работы изделий Р(tисп) ≥ 0,9 случайное число отказавших изделий рассчитывается на основании закона Пуассона (закона редких явлений): где а = (D / N) · n. 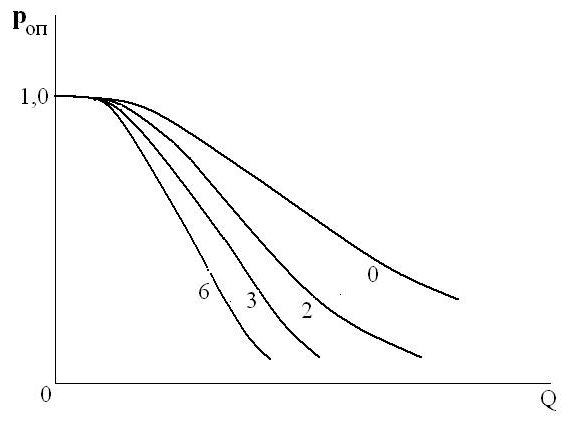 Рис 3. Оперативные характеристики для нескольких значений С при постоянном n На рис. 3 приведены оперативные характеристики pоп (Q) = p(d ≤ C). Как видно из графиков, чем больше приемочное число С, тем круче характеристика pоп (Q), то есть меньше различие между браковочным и приемочным уровнями показателя надежности, и, наоборот, чем меньше С, тем рассматриваемая кривая положе. Чрезвычайно важно следующее: чем выше надежность, то есть чем меньше Q, тем больший объем выборки требуется для подтверждения этого уровня надежности. Так, согласно таблице , при С = 2 и риске заказчика β =0,1 для подтверждения уровня надежности, соответствующего вероятности безотказной работы Р2 = 0,9, требуется выборка объемом n = 52. Если же необходимо подтвербить вероятность безотказной работы Р2 = 0,999, то необходимо – при тех же прочих условиях (β = 0,1; С = 2) – поставить на испытания выборку объемом n = 5320 изделий. Табл. № Объем выборки в зависимости от браковочной вероятности безотказной работы, приемочного числа С и риска β заказчика при Р* =0.9 и n/N≤0.1 (закон распределения Пуассона)
Браковочная вероятность Р2 соответствует некоторому гарантированному времени безотказной работы испытываемых изделий. Если закон распределения вероятности безотказной работы – экспоненциальный, то P2 (tг) = e xp(- λ · t г). (14) Время tг может быть очень велико. Для того, чтобы время испытаний было реальным (tи << tг), необходимо от вероятности Р2 перейти к вероятности Так как при реальных значениях параметров, входящих в формулу (6.15), правомерно приближение Пример. Составить план контроля надежности Р2= 0,95 на tг = 1000 ч при β = 0,1; tи = 200 ч; С = 1. Времени tг = 1000 ч согласно табл. соответствует объем выборки n = 76. По формуле (16) определяем Объем выборки можно уменьшить, если сузить поля допусков размеров критериальных параметров испытываемых объектов; нахождение этих параметров в заданных границах соответствует работоспособному состоянию изделия. Ужесточение допусков указанных размеров означает и ужесточение условий испытаний, вследствие чего увеличится доля изделий, у которых размеры характеризующих работоспособность параметров выйдут за допустимые пределы. Тем самым снизится показатель надежности (например, от 0,99 до 0,90) и – при прежних прочих условиях – уменьшится объем выборки. Ужесточающими (ускоряющими) факторами могут быть температура, электрическая нагрузка, вибрация и др. Здесь необходимо не только правильно выбрать критериальный параметр, значение которого связано с показателем надежности, но, главное, установить эту связь (зависимость от значений данного параметра значений показателя надежности). Последнее утверждение, по сути, выражает проблему ускоренных испытаний. Для того, чтобы извлечь полезную и адекватную информацию из результатов ускоренных испытаний, надо получить зависимость показателя надежности от изменения ускоряющего фактора. Предположим, что на основе собранных экспериментальных данных построен график, позволяющий «отобразить» множество значений интенсивностей λуj отказов в форсированных режимах на множество значений λнj (рис.4). Приведенный график позволяет ввести коэффициент ускорения где tн,у – время испытаний в нормальном и форсированном режимах соответственно.  Рис. 4 Значение коэффициента ускорения может быть найдено по результатам статистической обработки экспериментальных данных. Рассмотренный выше план контороля отражал только интересы заказчика (ведь учитывался только риск β приемки партии с недостаточно высоким уровнем надежности). Для отражения интересоа как заказчика, так и изготовителя задаются не только риском β (с соответствующим браковочным значением Р2 выроятности безотказной работы), но и риском α изготовителя и соответствующим ему приемочным значением Р1 ВБР. Вероятности β и α связаны с объемом выборки n, допустимыми уровнями дефектности и приемочным числом С формулами, полученными при использовании биноминального закона распределения: где d – число отказавших изделий в выборке объемом n (d меняется от нуля до С). Решая уравнения (18) и (19) относительно n и затем приравнивая первые части полученных выражений, находят зависимость приемочного числа С от заданных значений P1, P2,и. На основании этой зависимости можно построить таблицу, используемую при формировании плана контроля. В этой таблице #даются значения коэффициента А, вычисляемого по формуле Последовательность формирования плана контроля рассмотрим на примере. Дано : P1= 0,98 (при= 0,1) и P2= 0,9 (при= 0,1) на 500 часов испытания выборки из принимаемой партии изделий. Требуется рассчитать план контроля надежности. Порядок расчета: 1. Рассчитаем коэффициент А = ((1 – P2)(1+P1))/((1 – P1)(1+P2)) = 4,69 2. По найденному значению А и заданным значениям ис помощью таблиц определяем приемочное число С. Из соответствующих таблиц видно, что А лежит между числами 4,82 и 3,82. Если выбрать С = 2 (А = 4,82), то при заданных значениях,и P2 это приемочное число соответствует значению Р1, большему заданного. Если же выбрать С = 3 (А = 3,82), то приемочное число соответствует значению Р1, меньшему заданного. Учитывая, что значение А = 4,69 расположено ближе к табличному значению А = 4,82, чем к А = 3,82, выбираем С = 2. Для изготовителя это означает некоторое ужесточение плана контроля, так как должно быть обеспечено более высокое приемочное значение Р1 чем заданное. 3. По найденному значению С = 2 и заданным значениям Р2 = 0,9 и = 0,1 с помощью соответствующей таблицы определяем объем выборки n = 52 изделия. 4. Составляем план контроля для известного закона распределения контролируемого показателя надежности нет необходимости проводить испытание выборки в течение всего гарантированного времени. Предельную продолжительность испытания выбирают в зависимости от производственных и технико-экономических факторов (времени, которое может быть отведено на испытание, наличия необходимого качества образцов изделий и технических средств для проведения испытания). Таблица # При экспоненциальном законе распределения вероятности безотказной работы, который часто встречается на практике, браковочные значения вероятности, заданной на время tг, определяются по формуле (14) P2(tг) = e-λtг. Для времени испытания tивероятность безотказной работы P2'(tи) = e-λtи Прологарифмировав обе части уравнения (6.15) разделив второе на первое получим ln P2'(tи)/ ln P2(tг) = tи/tг или ln P2'(tи) = tи/tгln P2(tг) (21) Задаваясь различными значениями времени tииспытания при заданных значениях Р2и tг, по формуле (21) можно рассчитать соответствующие значения Р2' за это время. Зная Р2' и задаваясь значениямии С, нетрудно вычислить или определить из соответствующих таблиц необходимый объем выборки. Затем можно записать план контроля; n, tи, С. При d ≤ C партия изделий из которой взята выборка принимается; при d С партия бракуется. При планировании испытаний с учетом интересов не только заказчика, но и изготовителя для экспоненциального закона распределения вероятности безотказной работы план контроля по форме ничем не отличается от плана, рассмотренного ранее. Неизвестное значение Р1не представляет труда рассчитать по формуле (2.4), заменив Р2на Р1и Р2' на Р1' или определив их из соответствующих таблиц. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
