Курсовая работа Жураев У. Испытания на вязкость разрушения. Критерии вязкости разрушения. Расчет характеристик вязкости разрушения с использованием записи сигналов акустической эмиссии на оборудовании National Instruments
 Скачать 0.88 Mb. Скачать 0.88 Mb.
|
|
МИНИСТЕРСТВО ОБРАЗОВАНИЯ И НАУКИ РОССИЙСКОЙ ФЕДЕРАЦИИ ФЕДЕРАЛЬНОЕ ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ ВЫСШЕГО ОБРАЗОВАНИЯ «НАЦИОНАЛЬНЫЙ ИССЛЕДОВАТЕЛЬСКИЙ ТЕХНОЛОГИЧЕСКИЙ УНИВЕРСИТЕТ «МИСиС» ИНСТИТУТ НОВЫХ МАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ КАФЕДРА МЕТАЛЛОВЕДЕНИЯ И ФИЗИКИ ПРОЧНОСТИ НАПРАВЛЕНИЕ 22.03.01 МАТЕРИАЛОВЕДЕНИЕ И ТЕХНОЛОГИИ МАТЕРИАЛОВ Курсовая работа на тему: Испытания на вязкость разрушения. Критерии вязкости разрушения. Расчет характеристик вязкости разрушения с использованием записи сигналов акустической эмиссии на оборудовании National Instruments Студент ___Жураев У.Р. Группа БМТМ-17-1 Преподаватель Ожерелков Д.Ю. Оценка______________________________________________________ Москва 2021 СОДЕРЖАНИЕ ИНСТИТУТ НОВЫХ МАТЕРИАЛОВ И НАНОТЕХНОЛОГИЙ 0 КАФЕДРА МЕТАЛЛОВЕДЕНИЯ И ФИЗИКИ ПРОЧНОСТИ 0 НАПРАВЛЕНИЕ 22.03.01 МАТЕРИАЛОВЕДЕНИЕ И ТЕХНОЛОГИИ МАТЕРИАЛОВ 0 ВВЕДЕНИЕ 3 ВВЕДЕНИЕ В данной курсовой работе проводятся испытания на вязкость разрушения с целью определения величин, характеризующих нестабильное развитие трещины. Решающее значение имеет поведение трещины при нагружении, и возможность ее торможения В реальных изделиях всегда есть дефект или трещины, и в условиях эксплуатации металлические конструкции при напряжениях ниже предела текучести часто разрушаются хрупко из-за наличия различных концентраторов напряжений (механических надрезов, поверхностных и внутренних трещин, резких переходов по толщине сечения и др.) Их конструкционная прочность может оказаться значительно ниже, чем определенная методом статических испытаний, поэтому необходимы специальные испытания для оценки «чувствительности» материала к концентраторам напряжений. АНАЛИТИЧЕСКИЙ ОБЗОР ЛИТЕРАТУРЫ На основе теории хрупкого разрушения Гриффитса (анализ условий, при которых трещины будут развиваться как хрупкие – нестабильно, с большой скоростью) Ирвин сформулировал критерий перехода к нестабильному разрушению. Нестабильное разрушение наступает в тот момент, когда в материале у вершины трещины достигается критическая интенсивность напряжений. Кс [МПа×м1/2] – коэффициент интенсивности напряжений (является функцией только приложенных напряжений и геометрии трещины) K - коэффициент интенсивности напряжений, характеризует локальное повышение уровня растягивающих напряжений у вершины трещины Для практических целей оценки сопротивления разрушению наиболее важен коэффициент интенсивности напряжений в момент начала закритического развития трещины, когда ее длина достигает критической величины с. Значение коэффициента интенсивности напряжений (К) в момент перехода к нестабильному разрушению – критический коэффициент интенсивности напряжений (вязкость разрушения) – обозначают К1с – для плоскодеформированного состояния. Кс не является константой материала и зависит от толщины образца, что связано с изменением характера разрушения при увеличении толщины образца из-за изменения жесткости напряженного состояния по толщине и соответствующим изменением зоны пластической деформации у вершины трещины Вязкость разрушения при плоской деформации является константой материала К1с, т.е. не зависит от размеров и формы образцов К1с можно использовать для расчета критического напряжения при данном размере дефекта или, наоборот, предельно допустимого размера дефекта при заданном рабочем напряжении. Испытание на вязкость разрушения проводят по схеме внецентренного растяжения или трехточечного изгиба специальных образцов. Образцы имеют прямоугольное поперечное сечение и односторонний острый надрез, в вершине которого на пульсаторе наводится усталостная трещина. Для корректного определения К1с соотношения всех размеров образца, надреза и трещины должны обеспечивать условия плоской деформации у вершины трещины и упруго-напряженное состояние вдали от нее; На рисунке 1 изображены характерные типы диаграмм нагрузка-перемещение и методика их обработки  Рисунок 1 – Характерные типы диаграмм нагрузка-перемещение Диаграмма I типа характеризуется расположением вершины (точка С) левее прямой ОВ, наклоненной к оси v (или J) под углом ос5, тангенс которого на 5 % меньше тангенса угла, а наклона касательной ОА к начальному линейному участку диаграммы. Разрушение образца происходит в точке С диаграммы. Диаграмма II типа характеризуется наличием локального максимума нагрузки (точка D), находящегося левее прямой ОВ. Разрушение образца происходит в точке С диаграммы, расположенной левее прямой OG, наклоненной к оси v под углом, а 30, тангенс которого на 30 % меньше, чем тангенс угла наклона касательной ОА (угла а). Диаграмма III типа характеризуется наличием максимума нагрузки (точка Q), соответствующей разрушению образца, лежащей левее прямой OG. Диаграмма IV типа представляет собой кривую с максимальной нагрузкой в точке С. Разрушение образца происходит в точке F диаграммы, расположенной правее точки С. I тип: PQ = PC II тип: PQ = PD III тип: PQ = т. OB IV тип: PQ = т. OB МАТЕРИАЛ И МЕТОДИКА ИССЛЕДОВАНИЯ Определение характеристик трещиностойкости (вязкости разрушения) при статическом нагружении регламентируется ГОСТом 25.506-85, На рисунке 2 изображена схема образца на трехточечный (сосредоточенный) изгиб  Рисунок 2 – Схема образца на трехточечный (сосредоточенный) изгиб t = 0,5b b = 2t l = (0,45…0,55)b L=4b h = (0,25…0,45)b На рисунке 3 изображена схема образца на трехточечный (сосредоточенный) изгиб. 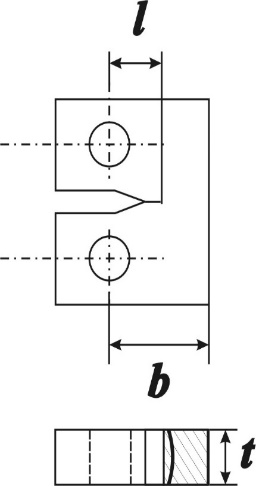 Рисунок 3 – Схема образца на внецентренное растяжение Основные требования к размерам b = 2t t = 0,5b l = (0,45…0,55)b Для определения характеристик трещиностойкости используют машины с механическим, гидравлическим или электрогидравлическим приводом, метрологические параметры которых соответствуют ГОСТу 28840—90. Испытательные машины должны быть аттестованы в соответствии с ГОСТом 24555—81. Для испытаний на трещиностойкость в данной работе использовалась машина Instron 5569. Для измерения смещений v или прогибов применяют двухконсольные датчики тензорезисторного типа. Захватные части датчиков, способы их установки на образцах и размеры элементов датчиков в зоне их крепления приведены на рисунках 4 и 5. 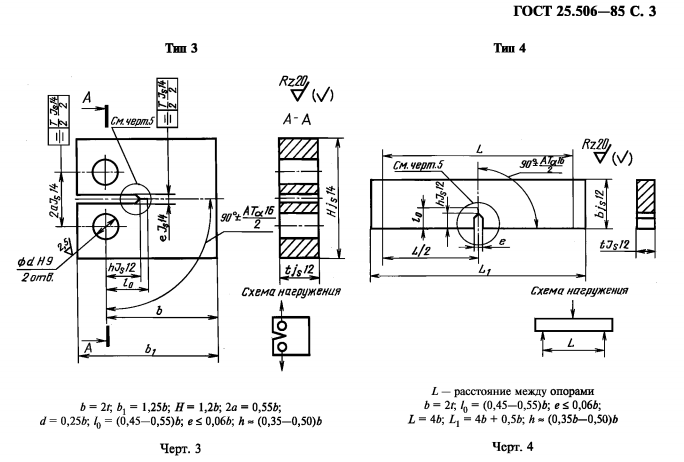 Рисунок 4  Рисунок 5 Метод акустической эмиссии – это метод испытаний, основанный на анализе параметров упругих волн акустической эмиссии, вызванных внутренними источниками, расположенными в толще исследуемого тела. Акустическая эмиссия (АЭ) – это акустическое излучение ультразвукового диапазона (∆ƒпримерно равен 100 МГц), сопровождающее процессы фазовых превращений, деформации и разрушения материалов. В лаборатории метод АЭ на базе National Instruments “LabView”. Также при испытании для оценки локальных напряжений дополнительно использовалась оптическая система VIC-3D РЕЗУЛЬТАТЫ И ИХ ОБСУЖДЕНИЕ Исходные данные В таблицах 1, 2 и 3 приведены данные, полученные из испытаний. Таблица 1 – Значения амплитуды акустической эмиссии в момент времени раскрытия датчика
Таблица 2 – Параметры образца
Таблица 3 – Физические величины для данного образца
Данные раскрытия датчика от приложенной нагрузки не приведены из-за большого количества значений. Расчеты и построение графиков Необходимо сопоставить данные акустической эмиссии с приложенной нагрузкой по времени. Графики зависимости раскрытия датчика от приложенной нагрузки, а также значения амплитуды акустической эмиссии в соответствующих точках представлены на рисунке 6.  Рисунок 6 Построив первичный график, выяснялось, что датчик АЭ не записывал с начального положения, поэтому было принято решение, что время, соответствующее максимальному значению амплитуды АЭ, будет равно времени, когда будет приложена максимальная нагрузка. Получившийся график более- менее приемлем, и возможно соответствует действительности. Для построения тангенса угла линейного участка были выбраны первая точка и точка, соответствующая нагрузке 400 Н. В таблице 4 приведены соответствующие значения. Таблица 4
 Для нахождения нагрузки, соответствующей нестабильному распространению трещины(PQ), необходимо построить тангенс, уменьшенный на 5% от линейного участка, и пресечение этой прямой и графика раскрытия датчика от приложенной нагрузки даст необходимую точку.  Рассчитав тангенсы наклонов для всех точек, найдём соответствующую нагрузку. PQ=494,41 Н. В таблице 5 указаны значения для построения прямой угла наклона β. Таблица 5
Для вычислений, которые понадобятся позже, была построена прямая, параллельная линейному участку и идущая в точку максимальной нагрузки. Максимальная нагрузка PС=930.783 Н. Начало прямой находится при νpс=0.07834 мм. νpс – условное пластическое смещение. В таблице 6 указаны значения для построения прямой параллельной линейному участку. Таблица 6
На рисунке 7 изображен график зависимости раскрытия датчика от приложенной нагрузки с построенными прямыми.  Рисунок 7 После нахождения соответствующих значений необходимо проверить критерии достоверности. Должно выполняться условие: 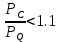 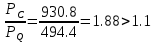 Критерий достоверности не выполняется Должно выполняться условие:  где νС и νQ − значение раскрытие датчика при максимальной нагрузке и нагрузке, соответствующей нестабильному распространению трещины соответственно. 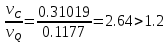 Критерий достоверности не выполняется. Найдем расчетное значение коэффициента интенсивности напряжений, и далее необходимо проверить критерий достоверности.   PQ – нагрузка в точке пересечения с 5%-ной касательной, Н L – расстояние между опорами, мм l – длина нанесенной трещины, мм t – ширина образца, мм b – толщина образца, мм Y – безразмерная гамма-функция отношения l/b u−коэффициент Пуассона E – модуль Юнга   Критерий достоверности:  β = 2,5 (стали, Al и Ti-сплавы) β = 0,6 (чугуны)  м <0.01м м <0.01мКритерий достоверности не выполняется В случае невыполнения условий корректности величин К1с, KQ трещиностойкость металлов оценивают по величинам Кс* δс, JQ. Необходимо для дальнейшего расчета рассчитать условный критический коэффициент интенсивности для образца данной толщины(K*C). Он также рассчитывается, как и KQ, только в формуле вместо PQ используется PC  Вычисление энергетической характеристики J1с производится по формуле  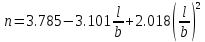 K*C – условный критический коэффициент интенсивности ν – коэффициент Пуассона E – модуль Юнга t – ширина образца b – толщина образца в месте надреза ApС – работа, затраченная на пластическое распространение трещины n – безразмерная функция отношения l/b  Работа, затраченная на пластическое распространение трещины, находится вычислением площади (интеграл) между графиком раскрытия трещины и прямой, параллельной линейному участку и проведенной от точки, соответствующей условному пластическому смещению, до точки максимальной нагрузки. На рисунке 8 представлена заштрихованная область, площадь которой необходимо вычислить.  Рисунок 8 С помощью программы OriginPro был вычислен интеграл до точки Vc. A1=0.1786 Дж Далее из него необходимо вычесть площадь треугольника, который находится ниже фигуры, для которой и считается площадь. Площадь треугольника найдем по формуле:  PC – максимальная нагрузка. P0 – нагрузка в начальном положении. νc – раскрытие датчика при максимальной нагрузке. νpс – условное пластическое смещение  Площадь искомой фигуры будет равна   Раскрытие в вершине трещины при максимальной нагрузке  K*C – условный критический коэффициент интенсивности ν – коэффициент Пуассона E – модуль Юнга σ0,2 – предел текучести rp – plastic rotation factor = 0.44 νpс – условное пластическое смещение z – начальное положение датчика l – длина нанесенной трещины b – толщина образца, мм 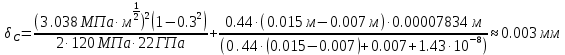 ВЫВОДЫ В данной работе при расчете следующие критерии достоверности не были выполнены: 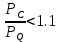 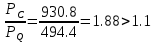  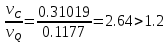   м <0.01м м <0.01мИсходя из этого, выбранные параметры образца не удовлетворяют для оценки вязкости разрушения. Следовательно, необходимо было провести испытания при большой толщине образца. В случае невыполнения условий корректности величин К1с, KQ трещиностойкость металлов также можно оценить по величинам Кс* δс, JQ  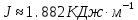 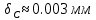 |
