Главная страница
Навигация по странице:

  • Решение (вариант 1)

  • Возможные ловушки и проблемы

  • Решение (вариант 2, с рисованием схемы)

  • Решение ( «обратный ход»)

    		•

    ege полякова 1. Использование и анализ информационных моделей (таблицы, диаграммы, графики)


    Скачать 1.12 Mb.
    НазваниеИспользование и анализ информационных моделей (таблицы, диаграммы, графики)
    Анкорege полякова 1
    Дата06.02.2022
    Размер1.12 Mb.
    Формат файлаdoc
    Имя файлаege1.doc
    ТипДокументы
    #352780
    страница8 из 8
    1   2   3   4   5   6   7   8

    Еще пример задания:


    Р-01. Таблица стоимости перевозок устроена следующим образом: числа, стоящие на пересечениях строк и столбцов таблиц, означают стоимость проезда между соответствующими соседними станциями. Если пересечение строки и столбца пусто, то станции не являются соседними. Укажите таблицу, для которой выполняется условие: «Минимальная стоимость проезда из А в B не больше 6». Стоимость проезда по маршруту складывается из стоимостей проезда между соответствующими соседними станциями.

    1)
    2)
    3)
    4)




    A
    B
    C
    D
    Е

    A






    3
    1



    B






    4



    2

    C
    3
    4






    2

    D
    1












    Е



    2
    2











    A
    B
    C
    D
    Е

    A






    3
    1
    1

    B






    4






    C
    3
    4






    2

    D
    1












    Е
    1



    2











    A
    B
    C
    D
    Е

    A






    3
    1
    4

    B






    4



    2

    C
    3
    4






    2

    D
    1












    Е
    4
    2
    2











    A
    B
    C
    D
    Е

    A









    1



    B






    4



    1

    C



    4



    4
    2

    D
    1



    4






    Е



    1
    2








    Решение (вариант 1):

    1. нужно рассматривать все маршруты из А в В, как напрямую, так и через другие станции

    2. рассмотрим таблицу 1:

    • из верхней строки таблицы следует, что из А в В напрямую везти нельзя, только через C (стоимость перевозки А-С равна 3) или через D (стоимость перевозки из А в D равна 1)
      A
      B
      C
      D
      Е

      A






      3
      1



    • предположим, что мы повезли через C; тогда из третьей строки видим, что из C можно ехать в В, и стоимость равна 4
      A
      B
      C
      D
      Е

      C
      3
      4






      2

    • таким образом общая стоимость перевозки из А через С в В равна 3 + 4 = 7

    • кроме того, из С можно ехать не сразу в В, а сначала в Е:
    A
    B
    C
    D
    Е

    C
    3
    4






    2

    а затем из Е – в В (стоимость также 2),




    A
    B
    C
    D
    Е

    Е



    2
    2






    так что общая стоимость этого маршрута равна 3  + 2 + 2 = 7

    • теперь предположим, что мы поехали из А в D (стоимость 1); из четвертой строки таблицы видим, что из D можно ехать только обратно в А, поэтому этим путем в В никак не попасть:
      A
      B
      C
      D
      Е

      D
      1












    • таким образом, для первой таблицы минимальная стоимость перевозки между А и В равна 7; заданное условие «не больше 6» не выполняется

    1. аналогично рассмотрим вторую схему; возможные маршруты из А в В:

    • , стоимость 7

    • , стоимость 7

    • таким образом, минимальная стоимость 7, условие не выполняется

    1. для третьей таблицы:

    • , стоимость 7

    • , стоимость 6

    • , стоимость 7

    • таким образом, минимальная стоимость 6, условие выполняется

    1. для четвертой:

    • , стоимость 9

    • , стоимость 8

    • минимальная стоимость 8, условие не выполняется

    1. условие «не больше 6» выполняется только для таблицы 3

    2. таким образом, правильный ответ – 3.

    Возможные ловушки и проблемы:

      • метод ненагляден, легко запутаться и пропустить решение с минимальной стоимостью

    Решение_(вариант_2,_с_рисованием_схемы)'>Решение (вариант 2, с рисованием схемы):

    1. для каждой таблицы нарисуем соответствующую ей схему дорог, обозначив стоимость перевозки рядом с линиями, соединяющими соседние станции:

    1)
    2)
    3)
    4)




    A
    B
    C
    D
    Е

    A






    3
    1



    B






    4



    2

    C
    3
    4






    2

    D
    1












    Е



    2
    2











    A
    B
    C
    D
    Е

    A






    3
    1
    1

    B






    4






    C
    3
    4






    2

    D
    1












    Е
    1



    2











    A
    B
    C
    D
    Е

    A






    3
    1
    4

    B






    4



    2

    C
    3
    4






    2

    D
    1












    Е
    4
    2
    2











    A
    B
    C
    D
    Е

    A









    1



    B






    4



    1

    C



    4



    4
    2

    D
    1



    4






    Е



    1
    2










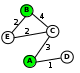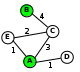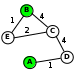    1. теперь по схемам определяем кратчайшие маршруты для каждой таблицы:

    1: или , стоимость 7

    2: или , стоимость 7

    3: , стоимость 6

    4: , стоимость 8

    1. условие «не больше 6» выполняется только для таблицы 3

    2. таким образом, правильный ответ – 3.

    Возможные ловушки и проблемы:

      • нужно внимательно строить схемы по таблицам, этот дополнительный переход (от табличных моделей к графическим) повышает наглядность, но добавляет еще одну возможность для ошибки

      • наглядность схемы зависит от того, как удачно вы выберете расположение ее узлов; один из подходов – сначала расставить все узлы равномерно на окружности, нарисовать все связи и посмотреть, как можно расположить узлы более удобно

      • по невнимательности можно пропустить решение с минимальной стоимостью

    Еще пример задания1:


    Р-00. Между четырьмя местными аэропортами: ВОСТОРГ, ЗАРЯ, ОЗЕРНЫЙ и ГОРКА, ежедневно выполняются авиарейсы. Приведён фрагмент расписания перелётов между ними:

    Аэропорт вылета Аэропорт прилета Время вылета Время прилета

    ВОСТОРГ ГОРКА 16:15 18:30

    ОЗЕРНЫЙ ЗАРЯ 13:40 15:50

    ОЗЕРНЫЙ ВОСТОРГ 14:10 16:20

    ГОРКА ОЗЕРНЫЙ 17:05 19:20

    ВОСТОРГ ОЗЕРНЫЙ 11:15 13:20

    ЗАРЯ ОЗЕРНЫЙ 16:20 18:25

    ВОСТОРГ ЗАРЯ 14:00 16:15

    ЗАРЯ ГОРКА 16:05 18:15

    ГОРКА ЗАРЯ 14:10 16:25

    ОЗЕРНЫЙ ГОРКА 18:35 19:50

    Путешественник оказался в аэропорту ВОСТОРГ в полночь (0:00). Определите самое раннее время, когда он может попасть в аэропорт ГОРКА.

    1) 16:15 2) 18:15 3)18:30 4) 19:50

    Решение («обратный ход»):

    1. сначала заметим, что есть прямой рейс из аэропорта ВОСТОРГ в ГОРКУ с прибытием в 18:30:

    ВОСТОРГ ГОРКА 16:15 18:30

    1. посмотрим, сможет ли путешественник оказаться в ГОРКЕ раньше этого времени, если полетит через другой аэропорт, с пересадкой; рассмотрим все остальные рейсы, который прибывают в аэропорт ГОРКА:

    ЗАРЯ ГОРКА 16:05 18:15

    ОЗЕРНЫЙ ГОРКА 18:35 19:50

    1. это значит, что имеет смысл проверить только возможность перелета через аэропорт ЗАРЯ (через ОЗЕРНЫЙ явно не получится раньше, чем прямым рейсом); для этого нужно быть в ЗАРЕ не позже, чем в 16:05

    2. смотрим, какие рейсы прибывают в аэропорт ЗАРЯ раньше, чем в 16:05:

    ОЗЕРНЫЙ ЗАРЯ 13:40 15:50

    1. дальше проверяем рейсы, который приходят в ОЗЕРНЫЙ раньше, чем в 13:40

    ВОСТОРГ ОЗЕРНЫЙ 11:15 13:20

    1. таким образом, мы «пришли» от конечного пункта к начальному, в обратном направлении

    2. поэтому оптимальный маршрут



    1. и правильный ответ – 2.

    Возможные ловушки и проблемы:

      • «напрашивается» ошибочный ответ 18:30 (прямой рейс)

      • при решении задачи «прямым ходом», с начального пункта, легко пропустить вариант с двумя пересадками

    1 Крылов С.С., Ушаков Д.М. ЕГЭ 2010. Информатика. Тематическая рабочая тетрадь. — М.: Экзамен, 2010.

    http://kpolyakov.spb.ru
    1   2   3   4   5   6   7   8

    написать администратору сайта