использование опрделённого интеграла в экономике. Использование определённого интеграла в эокономике
 Скачать 131.08 Kb. Скачать 131.08 Kb.
|
|
Федеральное Государственное общеобразовательное бюджетное учреждение Финансовый университет при Правительстве Российской Федерации (Финуниверситет) Московский финансовый колледж Проектная работа по дисциплине «Математика» На тему: «Использование определённого интеграла в эокономике» Выполнили Студентки 1 курса Группы 1Ф11 Лунина Алёна Рубель Мария Преподаватель: Ильина И.Д Москва 2016 Нет ни одной области математики, как бы абстрактна она ни была, которая когда-нибудь не окажется применимой к явлениям действительного мира. Н. И. Лобачевский
Символ введен Лейбницем (1675 г.). Этот знак является изменением латинской буквы S (первой буквы слова сумма). Экономический смысл определенного интеграла: выражает объем произведенной продукции при известной функции производительности труда.
Q = A * La * Kb Где А — технологический коэффициент, a — коэффициент эластичности по труду, а b — коэффициент эластичности по капиталу. Построить производственную функцию Кобба-Дугласа для оценки национального дохода США по следующим данным: Q–национальный доход США, млрд. долл., K – капиталовложения, млрд. долл., L – общее число занятых в экономике, тыс. чел.
Результаты множественной линейной регрессии ln Y = ln A + a ln K + b ln L представлены ниже Возвращаясь к исходным коэффициентам функции Кобба-Дугласа Q= AKαLβ , получим: lnA=0,862, A= 2,367. Таким образом, производственная функция имеет вид: Y=2,367*K0,956 L 0,129 .Это означает, что увеличении капиталовложений на 1% от своего среднего значения национальный доход США увеличивается на 0,956% от своего среднего значения, а при увеличении численности занятых в экономике на 1% от своего среднего значения национальный доход увеличится на 0,129 от своего среднего значения. 3. Кривая Лоренца Кривая Лоренца – кривая, которая демонстрирует фактическое деление доходов в обществе и дает наглядное представление о его отклонении от линии абсолютного равенства в делении доходов и о степени неравенства их деления.
По приведенным данным построена кривая Лоренца: 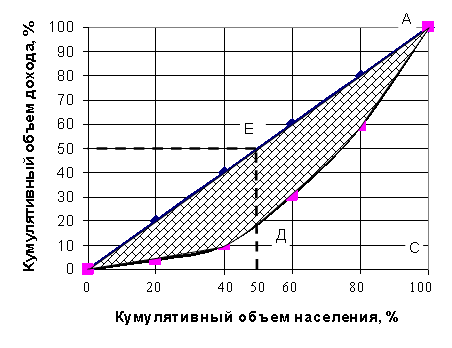 Проанализируем полученные результаты. Если совокупный доход и количество населения принять соответственно за 100%, точка А покажет, что 100% дохода распределено среди 100% населения, точка Е – 50% дохода приходится на 50% население и т.д. Линия ОЕА – абсолютное равенство в делении доходов, на которой в любой точке доход распределяется среди населения абсолютно равномерно. Графически прямая ОЕА делит квадрат на два ровных треугольника, боковые стороны которого характеризуют крайнюю степень имущественного неравенства (например, в точке С 100% доходу приходится на 1 получателя). Линии ОС и АС – это линии абсолютного неравенства; ОЕА – это линии абсолютного равенства. 4.Расчёт коэффициента Джини{\displaystyle Q=A\times L^{\alpha }\times K^{\beta }} 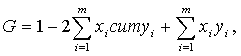 xi - доля доходов i-й группы в общей численности населения; yi - доля доходов, сосредоточенная уi-й группы населения; cum y i - кумулятивная доля дохода; m – число групп населения. Пример: Распределение населения региона по величине среднедушевого денежного дохода.
Определяем:
G =0,19174639.
это определение стоимости денежного потока путём приведения стоимости всех выплат к определённому моменту времени. Дисконтирование является базой для расчётов стоимости денег с учётом фактора времени. FV = PV * 1/(1+R) n
Пример: у вас появились «свободные» деньги, и вы пришли в банк, чтобы сделать вклад в размере, скажем, 2000 долларов. Сегодня положенные в банк 2000 долларов при банковской ставке 10% завтра будут стоить 2200 долларов, то есть 2000 долларов + проценты по вкладу 200 (=2000*10%). Получается, что через год вы сможете получить 2200 долларов. FV=$2000*(1+10%) или $2000*(1,10) = $2200. 6. Теорема о «средней» Формула конечных приращений или теорема Лагра́нжа о среднем значении утверждает, что если функция f{\displaystyle f} непрерывна на отрезке {\displaystyle [a;b]}[a;b] и дифференцируема в интервале {\displaystyle (a;b)}(a;b), то найдётся такая точка c ϵ (a;b){\displaystyle c\in (a;b)}, что 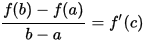 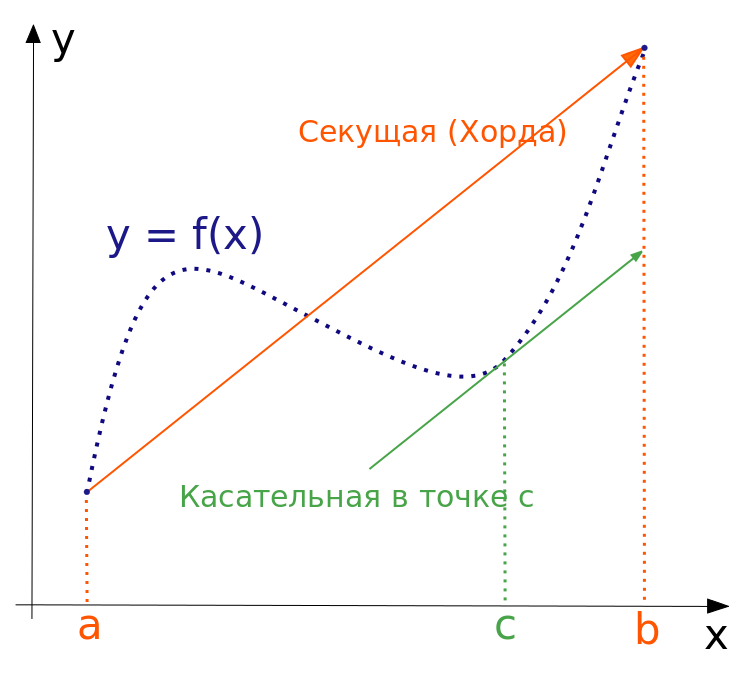 Степень доходности любой компании можно определить с помощью показателя рентабельности, который является основным показателем эффективности деятельности любой организации или предприятия. Рентабельность активов (англ. return on assets, ROA) – финансовый коэффициент, характеризующий отдачу от использования активов организации. Коэффициент показывает способность организации генерировать прибыль без учета структуры его капитала (финансового левериджа), качество управления активами и рассчитывается делением чистой прибыли NI (англ. Net Income) на величину всех активов (то есть сальдо баланса организации) AV (англ. Asset Value): 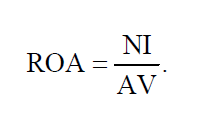 найдем значение параметра α: 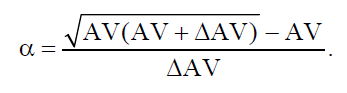 Итак, получили следующие формулы для коэффициентов факторного влияния: 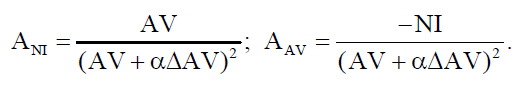 Пример: В качестве данных для анализа выбрано аудиторское заключение о годовой финансовой отчетности некоторой компании. 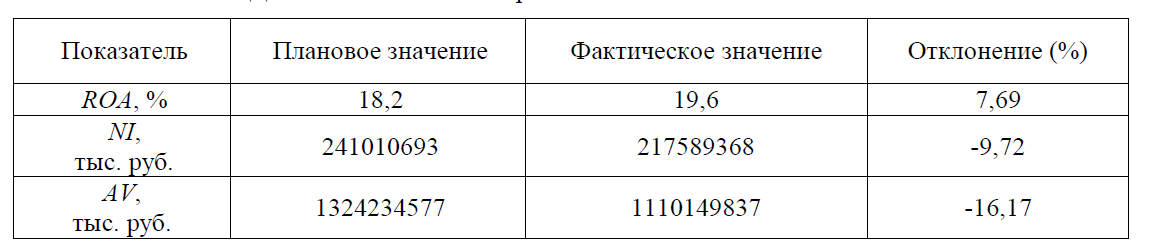 С помощью предыдущих формул определим значение параметра α и степень влияния факторов на конечное изменение результирующего показателя. α=0,522028, откуда ANI= 0,900779 *10 -9 AAV = -0,163942 *10-9 . Анализ данной модели показал, что значения влияния изменения факторов достаточно малы, однако, такие значения могут быть причиной значительных убытков предприятия. Анализ показал, что на отклонение величины рентабельности активов наиболее значительно повлияло изменение значения чистой прибыли. Так как рентабельность активов показывает сколько приходится прибыли на каждый рубль, вложенный в имущество организации, то проанализированные значения говорят о безоговорочной прибыльности исследуемой организации. Список литературы: http://eos.ibi.spb.ru/umk/8_1/15/15_P1_R2_T13.html http://vipreshebnik.ru/ekonomicheskaya-teoriya/208-zadacha-294-zadacha-po-krivoj-lorentsa.html http://www.std72.ru/dir/vysshaja_matematika/matematicheskie_metody_v_ehkonomike/tema_6_modeli_proizvodstva_i_potreblenija/165-1-0-2584 http://www.skachatreferat.ru/referaty/%D0%9F%D1%80%D0%B8%D0%BC%D0%B5%D0%BD%D0%B5%D0%BD%D0%B8%D0%B5-%D0%B2-%D0%AD%D0%BA%D0%BE%D0%BD%D0%BE%D0%BC%D0%B8%D0%BA%D0%B5-%D0%9E%D0%BF%D1%80%D0%B5%D0%B4%D0%B5%D0%BB%D0%B5%D0%BD%D0%BD%D0%BE%D0%B3%D0%BE-%D0%98%D0%BD%D1%82%D0%B5%D0%B3%D1%80%D0%B0%D0%BB%D0%B0/122760.html | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
