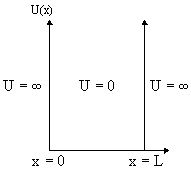Шпаргалки Квантовая физика. Испускание электронов веществом под действием света называется

• Название: Испускание электронов веществом под действием света называется
• Дата: 21.05.2018
• Размер: 0.49 Mb.
• Имя файла: Шпаргалки Квантовая физика.docx
• Тип: Документы; #44440
• страница: 2 из 5

7.Формула Релея-Джинса. Формула Планка.

Закон Релея - Джинса - закон излучения Рэлея - Джинса для равновесной плотности излучения абсолютно чёрного тела u(ω,T) и для испускательной способности абсолютно чёрного тела f(ω,T) который получили Релей и Джинс, в рамках классической статистики о равнораспределении энергии по степеням свободы. Формула Релея-Джинса:

, kT – средняя энергия осциллятора с собственной частотой w

Формула справедлива только в области малых частот и не согласуется с законом Вина.  Итак, было получено две формулы, описывающие излучение абсолютно черного тела: одна для коротковолновой части спектра (формула Вина), другая – для длинноволновой (формула Рэлея–Джинса). Задача состояла в том, чтобы получить выражение, описывающее тепловое излучение во всем диапазоне частот.

Согласно квантовой теории Планка, атомные осцилляторы излучают энергию не непрерывно, а определенными порциями -- квантами, причем энергия кванта пропорциональна частоте колебания , где -- постоянная Планка. Т.к. излучение испускается порциями, то энергия осциллятора (стоячей волны) может принимать лишь определенные дискретные значения, кратные целому числу эл-тарн порций энергии : (n=0,1,2,…).

Ф-ла Планка - выражение для спектральной плотности энергетической светимости абсолютно чёрного тела.



формула Планка дает исчерпывающее описание равновесного теплового излучения.

8. Волны де Бройля

В 1924г. Луи де Бройль пришел к выводу, что двойственность света должна быть распространена и на частицы вещества - электроны. Гипотеза де Бройля: электрон, корпускулярные свойства которого (заряд, масса) изучаются давно, имеет еще и волновые свойства, т.е. при определенных условиях ведет себя как волна.

Количественные соотношения, связывающие корпускулярные и волновые свойства частиц, такие же, как для фотонов.



Идея де Бройля состояла в том, что это соотношение имеет универсальный характер, справедливый для любых волновых процессов. Любой частице, обладающей импульсом р, соответствует волна, длина которой вычисляется по формуле де Бройля.

 - волна де Бройля

p =mv- импульс частицы, h - постоянная Планка.

Волны де Бройля, которые иногда называют электронными волнами, не являются электромагнитными.

Свойства волн де Бройля

Пусть частица массы m движется со скоростью v. Тогда фазовая скорость волн де Бройля



.

Т.к. c > v, то фазовая скорость волн де Бройля больше скорости света в вакууме ( v_ф может быть больше и может быть менше с, в отличие от групповой ).

Групповая скорость

Групповая скорость волн де Бройля волны перемещаются вместе с частицей, следовательно, групповая скорость волн де Бройля равна скорости движения частицы.

Одно из свойств волн де Бройля – они обладают дисперсией т.е. зависит от частоты

9. Принцип неопределенности Гейзенберга

Микрочастицы в одних случаях проявляют себя как волны, в других как корпускулы. К ним не применимы законы классической физики частиц и волн. В квантовой физике доказывается, что к микрочастице нельзя применять понятие траектории, но можно сказать, что частица находится в данном объеме пространства с некоторой вероятностью Р. Уменьшая объем, мы будем уменьшать вероятность обнаружить частицу в нем. Вероятностное описание траектории (или положения) частицы приводит к тому, что импульс и, следовательно, скорость частицы может быть определена с какой-то определенной точностью.

            Далее, нельзя говорить о длине волны в данной точке пространства и отсюда следует, что если мы точно задаем координату Х, то мы ничего не сможем сказать о импульсе частицы, т.к. . Только рассматривая протяженный участок  мы сможем определить импульс частицы. Чем больше , тем точнее р и наоборот, чем меньше , тем больше неопределенность в нахождении р.

            Соотношение неопределенностей Гейзенберга устанавливает границу в одновременном определении точности канонически сопряженных величин, к которым относятся координата и импульс, энергия и время.

            Соотношение неопределенностей Гейзенберга: произведение неопределенностей значений двух сопряженных величин не может быть по порядку величины меньше постоянной Планка h









Это значит, что чем более точно мы определяем положение частицы, тем меньше можем знать о ее импульсе, и наоборот.

Таким образом. для микрочастицы не существует состояний, в которых её координата и импульс имели бы одновременно точные значения. Чем меньше неопределенность одной величины, тем больше неопределенность другой.

            Соотношение неопределенностей является квантовым ограничением применимости классической механики к микрообъектам.



следовательно, чем больше m, тем меньше неопределенности в определении координаты и скорости.

10. Уравнение Шредингера. Свободная частица. Свободная частица на замкнутой траектории.

Уравнение Шредингера описывает изменение во времени состояния квантового объекта, характеризуемого волновой функцией. Если известна волновая функция Ψ в начальный момент времени, то решая уравнение Шредингера, можно найти Ψ в любой последующий момент времени t. Уравнение Шредингера для частицы массой m, движущейся со скоростью, много меньшей скорости света в вакууме, под действием силы, порождаемой потенциалом U(x,y,z,t):

где i мнимая единица, дельта – оператор Лапласа. Ψ(x,y,z,t) – временная волновая функция частицы, которая зависит от координат и времени. Уравнение содержит производную от функции Ψ по времени и называется временным(нестационарным) уравнением Шредингера.

Стационарными состояниями называют состояния, в которых все наблюдаемые величины не изменяются с течением времени. В частности не изменяется со временем плотность вероятности |Ψ(r,t)|². Стационарные решения уравнения Шредингера имеют смысл для тех задач, в которых силовое поле потенциально и следовательно, потенциальная энергия U не зависит от времени U=U(x,y,z).

В стационарных состояниях состояние частицы в данный момент времени описывается периодической функцией времени Ψ с циклической частотой ω. При этом Ψ-функция определяется полной энергией частицы: При таком виде пси-функции плотность вероятности Р остается постоянной Р=ΨΨ^*

Стационарное уравнение Шредингера записывают в виде:

Потенциальная энергия здесь задается классически, как если бы никакими волновыми свойствами частица не обладала.

Частица называется свободной, если на нее не действуют силовые поля, т.е. U = 0.

            Уравнение Шредингера для стационарных состояний в этом случае:

                                      

Его решение: Ψ(x)=Ае ^ikx , где А = const, k = const

И собственные значения энергии:

             

Т.к. k может принимать любые значения, то, следовательно,  и Е принимает любые значения, т.е. энергетический спектр будет сплошным.

            Временная волновая функция

                        (-  уравнение волны)

т.е. представляет плоскую монохромную волну де Бройля.

11. Частица в бесконечно глубокой потенциальной яме

Рис. 1. Потенциальная яма

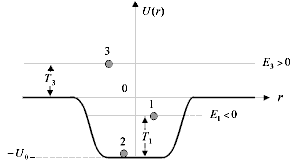
Потенциальная яма – ограниченная область пространства с пониженной потенциальной энергией частицы.
Энергия частицы Е = сумма её кинетической энергии Т  > 0 и потенциальной U (положит. или отриц.). Если частица находится внутри ямы, то её кинетическая энергия Т₁ меньше глубины ямы U₀, энергия частицыЕ₁ = Т₁ + U₁ = Т₁ - U₀ < 0 и частица не может покинуть яму (находится в связанном состоянии). Она двигается в ней с кинетической энергией Т₁, отражаясь от стенок. Если частица находится на дне ямы, то её кинетическая энергия Т₂ = 0 и Е₂ = -U₀ < 0(частица лежит на дне ямы). Это положение частицы наиболее устойчиво. Если частица вне ямы имела кинетическую энергию Т₃ то она беспрепятственно пересекает яму, преодолевая её с возросшей кинетической энергией Т₃ + U₀.
       Пример потенциальной ямы – ядерная яма глубиной 40- 50 МэВ и шириной 10^-13–10^-12 см, в которой на различных уровнях находятся нуклоны, двигающиеся со средней кинетической энергией20 МэВ.

Рис. 2. Бесконечная прямоугольная потенциальная яма.

Итак, пусть частица массы m находится в одномерной потенциальной яме бесконечной глубины (рис. 2). Потенциальная энергия U удовлетворяет следующим граничным условиям

.

(1)

При таких граничных условиях частица находится внутри потенциальной ямы 0 < x < L и не может выйти за ее пределы, т.е.

ψ(x) = 0       x < 0, x > L

(2)

    Для бесконечной одномерной потенциальной ямы имеем следующее:

1. 
   Энергия частицы принимает определенные дискретные значения. Обычно говорят, что частица находится в определенных энергетических состояниях.где n = 1, 2, 3...
   
2. 
   Частица может находиться в каком-то одном из множества энергетических состояний.
   
3. 
   Частица не может иметь энергию равную нулю.
   
4. 
   Каждому значению энергии E_n соответствует собственная волновая функция ψ_n, описывающая данное состояние.
   

Для собственной функции ψ₁(x) вероятность обнаружить частицу в точке x = L/2 максимальна. Для ψ₂(x) вероятность обнаружения частицы в этой точке 0

12. Квантовый осциллятор.

      Гармоническим осциллятором называют частицу, совершающую одномерное движение под действием квазиупругой силы 

Потенциальная энергия частицы



   Гармонический осциллятор в квантовой механике описывается уравнением Шредингера:

Значения Ψ-функции мы находить не будем. Нас интересуют значения полной энергии осциллятора:

где n = 0, 1, 2…

Рис. 5.3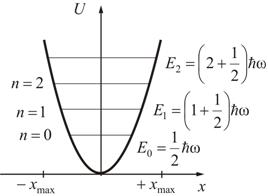


 не зависит от n, в отличие от прямоугольной потенциальной ямы, рассмотренной нами в п. 5.2.

       Минимальная энергия  называется нулевой энергией, т.е. при T=0  колебания атомов К в кристаллической решетке не прекращаются.

       В квантовой механике вычисляется вероятность различных переходов квантовой системы из одного состояния в другое. Для гармонического осциллятора возможны лишь переходы между соседними уровнями.

       Условия, накладываемые на изменения квантовых чисел при переходах системы из одного состояния в другое, называются правилами отбора. Для гармонического осциллятора правило выражено формулой:

 .

  Энергия квантового осциллятора изменяется только порциями, т.е. квантуется. Причем, как и в прямоугольной яме, энергия ограничена снизу минимальным значением