Шпаргалки Квантовая физика. Испускание электронов веществом под действием света называется

• Название: Испускание электронов веществом под действием света называется
• Дата: 21.05.2018
• Размер: 0.49 Mb.
• Имя файла: Шпаргалки Квантовая физика.docx
• Тип: Документы; #44440
• страница: 3 из 5

13. Туннельный эффект

Туннельный эффект – прохождение частицы (или системы) сквозь область пространства, пребывание в которой запрещено классической механикой. Наиболее известный пример такого процесса – прохождение частицы сквозь потенциальный барьер, когда её энергия Е меньше высоты барьера U₀. В классической физике частица не может оказаться в области такого барьера и тем более пройти сквозь неё, так как это нарушает закон сохранения энергии. Однако в квантовой физике ситуация принципиально другая. Квантовая частица не движется по какой-либо определенной траектории. Поэтому можно лишь говорить о вероятности нахождения частицы в определенной области пространства ΔрΔх > ћ.При этом ни потенциальная, ни кинетическая энергии не имеют определенных значений в соответствии с принципом неопределенности.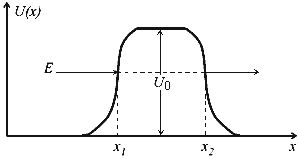

     Возможность прохождения частицы сквозь потенциальный барьер обусловлена требованием непрерывной волновой функции на стенках потенциального барьера. Вероятность обнаружения частицы справа и слева связаны между собой соотношением, зависящим от разности E - U(x) в области потенциального барьера и от ширины барьера x₁ - x₂ при данной энергии.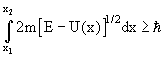



    С увеличением высоты и ширины барьера вероятность туннельного эффекта экспоненциально спадает. Вероятность туннельного эффекта также быстро убывает с увеличением массы частицы.
    Проникновение сквозь барьер носит вероятностный характер. Частица с Е < U₀, натолкнувшись на барьер, может либо пройти сквозь него, либо отразиться. Суммарная вероятность этих двух возможностей равна 1.

Примеры: альфа-распад, холодная эмиссия электронов из металлов, явления в контактном слое двух полупроводников и т.д.

14.Планетарная модель атома по Резерфорду.

Э.Резерфорд предложил планетарную модель атома, согласно которой ядро находится в центре атома, а электроны вращаются вокруг ядра подобно планетам вокруг Солнца. Заряды электронов уравновешиваются положительным зарядом ядра, и атом в целом остается-электронейтральным.

Возникающая вследствие вращения электронов центробежная сила уравновешивается электростатическим притяжением электронов к противоположно заряженному ядру.
Опыты Резерфорда и его сотрудников привели к выводу, что в центре атома находится плотное положительно заряженное ядро, диаметр которого не превышает 10^-14–10^-15 м. Это ядро занимает только десятую-двенадцатую часть полного объема атома, но содержит весь положительный заряд и не менее 99,95 % его массы. Веществу, составляющему ядро атома, следовало приписать колоссальную плотность порядка ρ ≈ 1015 г/см3. Заряд ядра должен быть равен суммарному заряду всех электронов, входящих в состав атома. Впоследствии удалось установить, что если заряд электрона принять за единицу, то заряд ядра в точности равен номеру данного элемента в таблице Менделеева.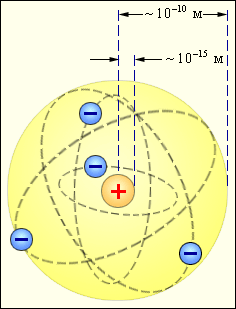

Опыты по рассеянию α-частиц позволили не только установить существование атомного ядра, но и определить его заряд. Оказалось, что положительный заряд ядра атома численно равен порядковому номеру элемента в периодической системе. Следовательно, порядковый номер элемента не просто регистрирует его положение в периодической системе, а является важнейшей константой элемента, выражающей положительный заряд ядра его атома. Из электронейтральности атома следует, что и количество вращающихся вокруг ядра электронов равно порядковому номеру элемента. Таков физический смысл порядкового номера элемента в Периодической системе элементов.

15. Модель атома по Бору. Опыт Франка-Герца.

Энергия электрона зависит от радиуса его орбиты. Минимальная энергия у электрона, который находится на ближайшей к ядру орбите. При поглощении кванта энергии электрон переходит на орбиту с более высокой энергией (возбужденное состояние). И наоборот, при переходе с высокого энергетического уровня на более низкий - электрон отдает (излучает) квант энергии.

Кроме того, Бор указал, что разные энергетические уровни содержат разное количество электронов: первый уровень - до 2 электронов; второй уровень - до 8 электронов…

Бор высказал предположения, которые были названы постулатами Бора.

Первый постулат(постулат стационарных состояний): электроны движутся только по определенным (стационарным) орбитам. При этом, даже двигаясь с ускорением, они не излучают энергию.

Второй постулат(правило частот): излучение и поглощение энергии в виде кванта света (hn) происходит лишь при переходе электрона из одного стационарного состояния в другое. Величина светового кванта равна разности энергий тех стационарных состояний, между которыми совершается скачок электрона: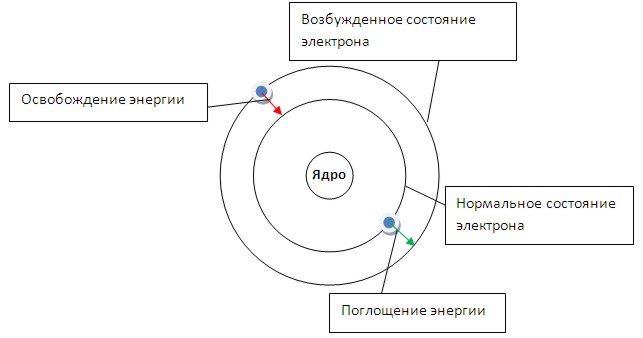


Опыты франка:

опыт, явившийся экспериментальным доказательством дискретности внутренней энергии атома

лектроны ускорялись разностью потенциалов U между катодом и сеткой. Эту разность потенциалов можно было изменять с помощью потенциометра П. Между сеткой и анодом тормозящее поле 0,5 В (метод задерживающих потенциалов).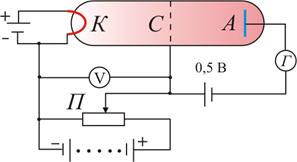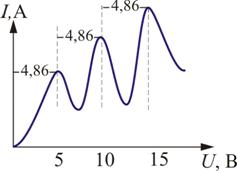


опыт Франка — Герца показал, что спектр поглощаемой атомом энергии не непрерывен, а дискретен, минимальная порция (квант электромагнитного поля), которую может поглотить атом Hg, равна 4,9 эВ. Значение длины волны λ = 253,7 нм свечения паров Hg, возникавшее при V > 4,9 В, оказалось в соответствии со вторым постулатом Бора

Из опыта следует, что при увеличении ускоряющего потенциала вплоть до 4,86 В анодный ток возрастает монотонно, его значение проходит через максимум (4,86 В), затем резко уменьшается и возрастает вновь

Таким образом, опыты Франка и Герца экспериментально подтвердили не только первый, но и второй постулат Бора и сделали большой вклад в развитие атомной физики.

16. Уравнение Шредингера для атома водорода

Уравнение Шредингера, примененное к атому водорода, позволяет получить результаты боровской теории атома водорода без привлечения постулатов Бора и условия квантования. Квантование энергии возникает как естественное условие, появляющееся при решении уравнения Шредингера, в некотором смысле аналогичное причине квантования энергии для частицы в потенциальной яме. Применить стационарное уравнение Шредингера к атому водорода:

1) подставить в это уравнение выражение для потенциальной энергии взаимодействия электрона с ядром



б) в качестве m подставить m_e - массу электрона).

После этого получим уравнение Шредингера для атома водорода:



Так как потенциальная энергия зависит только от r, решение уравнения удобно искать в сферической системе координат: r, θ, φ.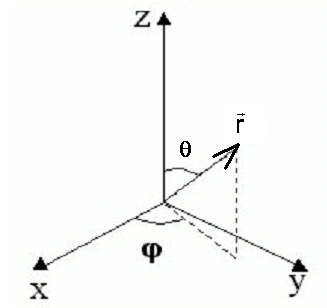



Волновая функция в этом случае будет функцией от r, θ и φ, т.е.



Оператор Лапласа   необходимо записать в сферических координатах, т.е. выразить через производные по r, θ и φ.

Что бы решение уравнения Шредингера для атома водорода существует при следующих условиях:

а) при любых положительных значениях полной энергии (E > 0). Это так называемые несвязанные состояния электрона, когда он пролетает мимо ядра и уходит от него на бесконечность;

б) при дискретных отрицательных значениях энергии



Эта формула совпадает с полученной Бором формулой для энергии стационарных состояний атома водорода. Целое число n называют главным квантовым числом.

17. Квантование момента импульса, проэкции момента импульса. Эффект Зеемана.

Момент импульса. Момент импульса М является одной из важнейших характеристик движения. Однако в квантовой теории момент импульса существенно отличается от классического. А именно, модуль момента импульса может быть задан сколь угодно точно только с одной из проекций, например, Мг. Другие две проекции оказываются полностью неопределенными.

Это означает, что направление момента М в пространстве является неопределенным. Наглядно подобную ситуацию можно попытаться представить так: вектор М как-то «размазан» по образующим конуса, ось которого совпадает с направлением координатной оси Z. В этом случае вполне определенное значение имеет лишь проекция Мг. Другие две проекции, Мх и Му, оказываются полностью неопределенными.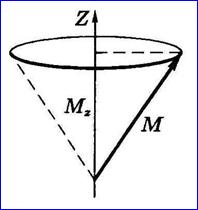



Модуль момента импульса. Для определения квадрата момента необходимо решить уравнение

(12.51)

Оператор достаточно сложный, и решение этого уравнения является очень громоздким. Поэтому ограничимся приведением окончательных результатов, причем только для собственных значений данного оператора:

М2 = l( l + 1)ћ2, l = 0, 1, 2, …,

(12.52)

где l — орбитальное (или азимутальное) квантовое число. Отсюда модуль момента

l = 0, 1, 2, …,(n-1).

(12.53)

Видно, что эта величина является дискретной (квантованной).

Следует отметить, что между классическим моментом импульса и соответствующим ему оператором имеется существенное различие. Классический момент [r р] зависит от выбора точки О, относительно которой берется радиус-вектор r. Оператор же момента импульса не зависит от выбора точки О (в этом можно убедиться, записав проекции момента в сферических координатах). Оператор момента импульса зависит только от направления координатных осей. Поэтому его называют оператором углового момента. Собственные значения операторов квадрата и проекции углового момента, и  также не зависят от выбора точки О.

Проекция момента М z. Рассмотрим решение уравнения

(12.54)

 В сферических координатах (r, θ, φ) оператор проекции момента импульса на полярную ось z (от которой отсчитывается полярный угол θ) имеет вид

(12.54)

Для определения собственных значений и собственных функций этого оператора надо, согласно , решить уравнение

(12.55)

где φ – азимутальный угол в полярной системе координат.

Подстановка ψ = C exp (αφ) приводит после сокращения на общий множитель ехр (αφ) к алгебраическому уравнению, 



из которого α = iМ z /ћ. Значит, решение уравнения таково:

(12.56)

Эта функция конечна, непрерывна и гладкая. Она должна быть и однозначной, для чего должно быть выполнено условие ψ (φ + 2π) = ψ (φ) или

Это условие будет выполнено, если положить M z = mћ, где т —целое положительное или отрицательное число либо нуль. Следовательно, оператор  обладает дискретным спектром:

Mz = m ħ, m = 0, ± 1, ± 2, …

Эффектом Зеемана называется расщепление энергетических уровней или спектральных линий излучения атомов, молекул или кристаллов, помещенных в магнитное поле. Этот эффект впервые был предсказан Г.А. Лоренцем в 1895 г. и экспериментально был подтвержден в 1896 г. П. Зееманом при исследовании спектров испускания натриевой горелки, помещенной в магнитное поле. Он обнаружил три спектральных линии (триплет) при наблюдении в направлении, перпендикулярном магнитному полю, и две линии (дублет) при наблюдении вдоль магнитного поля, вместо ожидавшейся одной спектральной линии. Такой характер расщепления линий получил название нормального эффекта Зеемана в отличие от позже обнаруженного и гораздо чаще наблюдаемого аномального эффекта - более сложной картины расщепления спектральных линий.

Если поместить атом в магнитное поле, то его энергетические уровни (термы) изменяются. Изменение энергии связано с взаимодействием магнитного момента рассматриваемого состояния атома с внешним магнитным полем, а его величина в случае слабого поля равна скалярному произведению вида (в системе СГС)

Где м - магнитный момент состояния атома, Н - напряженность магнитного поля. Магнитный момент терма пропорционален его полному механическому моменту M_Jсоставляющих его электронов и в рамках векторной модели атома может быть представлен в виде:

где мв = 9.273 -10^-21 эрг/Гс - магнетон Бора, g_J - фактор Ланде или g - фактор.

Проекция M_Jz полного механического момента M_J на какое-либо направление (например, направление магнитного поля H - ось OZ) квантуется, т. е. может принимать лишь строго определенные значения, а именно M_Jz = 0, ±1, .., ±J. Поскольку энергия взаимодействия магнитного момента с магнитным полем зависит от величины проекции момента m·h, то уровень с моментом M_J в присутствии магнитного поля расщепляется на 2J + 1 компоненту. Говорят, что магнитное поле снимает вырождение уровня по магнитному квантовому числу m = 0, ±1, .., ±J. Изменение энергии для каждой компоненты уровня:

Это расщепление симметрично относительно начального нерасщепленного уровня, а абсолютная величина определяется g-фактором и магнитным полем Н. Величина g- фактора существенно зависит от типа связи электронов в атоме (LS- или jj-тип) и в случае чистой LS-связи равна: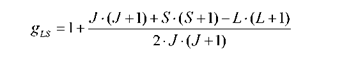