ТАу. Курсовая работа Фадеев П.А. ПС-33. Исследование асу на устойчивость работы по алгебраическим и частотным критериям
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
3 .Расчет и построение частотных характеристик систем. 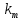 ; ; 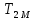 ; ; 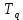 и и 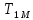 по варианту №14. по варианту №14. С учетом числовых значений для данного варианта: 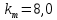 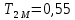 с с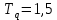 с с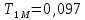 с с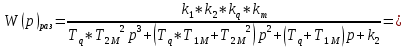 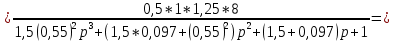 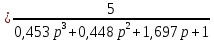 Для получения аналитических выражений ЧХ исследуемой системы производим формальную замену оператора Р на 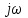 , тогда имеем , тогда имеем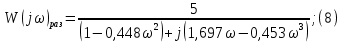 Умножим и разделим числитель и знаменатель на комплексное число, сопряженное знаменателю: 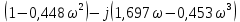 Отсюда получим: 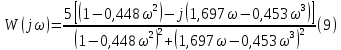 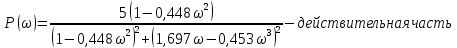 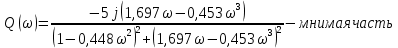 Таблица-3. Результаты расчета
 Рисунок – 6. Вещественная частотная характеристика  Рисунок – 7. Мнимая частотная характеристика 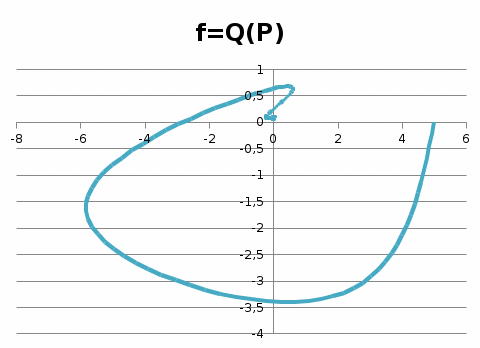 Рисунок 8. АФЧХ инерционного звена, построенная по данным 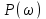 и и 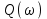 Для определения устойчивости системы по критериям Гурвица и Михайлова необходимо найти характеристическое уравнение для замкнутой системы. Ранее была получена передаточная функция для разомкнутой системы. 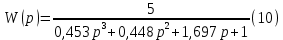 Для замкнутой АС с отрицательной обратной связью передаточная функция будет равна: 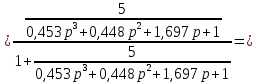 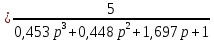 Где знаменатель есть характеристическое уравнение для замкнутой АС, т.е. 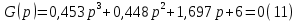 3.1 Определение устойчивость по критерию Михайлова В характеристическое уравнение для замкнутой АС вместо оператора р поставим значение jω, получим: 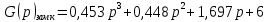 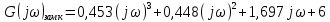 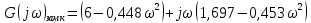 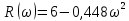 -действительная часть -действительная часть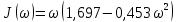 – мнимая часть – мнимая частьДавая различные значения ω в пределах ωЄ(0,∞), найдем координаты R(ω) , J(ω)точек годографа комплексного коэффициента передачи. Таблица-4. Результаты расчета по критерий Михайлова
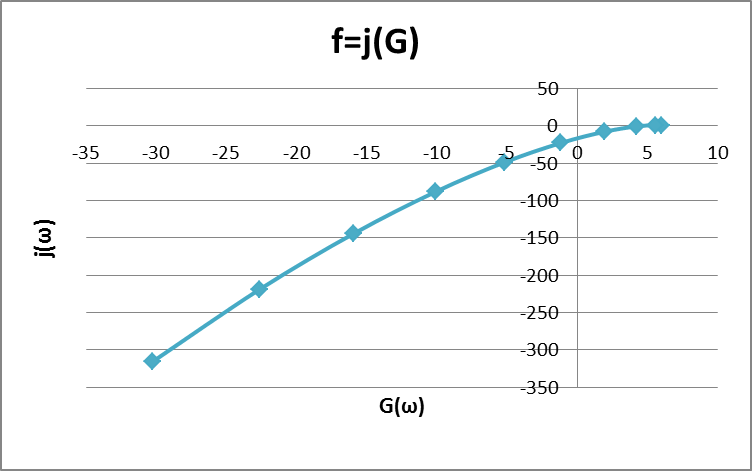 Рисунок – 9. Диаграмма по критерий Михайлова 3.2 Определение устойчивость по критерию Гурвица Для того чтобы САР могла нормально функционировать, она должна, прежде всего, удовлетворять требованиям устойчивости. Система является устойчивой, если она возвращается к установившемуся состоянию после прекращения действия возмущения, которое вывело ее из этого состояния. Общее решение X(t) дифференциального уравнения линейной системы управления может быть представлено в виде суммы двух функций времени. 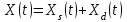 , (12) , (12)из которых Xs(t) характеризует так называемое вынужденное движение системы и зависит от внешнего воздействия, а X 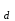 (t) определяет свободное движение или переходный процесс в системе. (t) определяет свободное движение или переходный процесс в системе.Математическая форма записи условия устойчивости представляет собой требование обращения в нуль Xd(t) при неограниченном возрастании времени с момента начала переходного процесса, т.е. 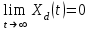 . (13) . (13)Функция Xd(t), являющаяся общим решением соответствующего дифференциального уравнения для линейной системы n-го порядка, имеет вид [2] 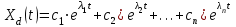 , (14) , (14)где C1, C2, …, Cn - постоянные интегрирования, а 1, 2, …, n - неравные корни характеристического уравнения системы управления. Из выражения 13 видно, что при t 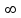 Xd(t) будет стремиться к нулю только в том случае, если все nкорней характеристического уравнения имеют отрицательные вещественные части. Xd(t) будет стремиться к нулю только в том случае, если все nкорней характеристического уравнения имеют отрицательные вещественные части.Следовательно, для суждения об устойчивости САР нет необходимости определять значения корней характеристического уравнения, что связано обычно с трудоемкими вычислениями. Достаточно располагать косвенными признаками, которые позволяли бы судить об отсутствии в характеристическом уравнении системы корней с неотрицательной вещественной частью (действительные корни могут рассматриваться как частный случай комплексных с нулевой мнимой частью). Такие признаки получили название критериев устойчивости. Известно, что для системы n-го порядка характеристическое уравнение имеет вид многочлена n-й степени [4 – 5]. 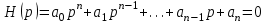 (15) (15)Критерий Гурвица. Проверка устойчивости по Гурвицу сводится к вычислению по коэффициентам характеристического уравнения так называемых определителей Гурвица, которые для устойчивой системы должны быть положительными. Для получения определителей Гурвица составляется таблица их коэффициентов характеристического уравнения n-й степени.  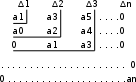 Правила составления таблицы просты: по главной диагонали выписываются по порядку n коэффициентов характеристического уравнения от a1 до an; каждая строка содержит n элементов; строки с нечетными и четными индексами чередуются; недостающие элементы строк заполняются нулями. Отчеркивая соответствующие строки и столбцы, получают n определителей Гурвица. 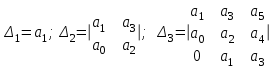 и т.д. и т.д.Критерий устойчивости Гурвица заключается в требовании положительности всех n определителей (при ao>0), т.е. 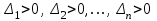 Необходимым (но недостаточным) условием устойчивости системы n порядка при ao>0 является требование положительности всех коэффициентов характеристического уравнения 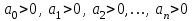 Поскольку последнее условие легко проверяется по виду уравнения, записанного с конкретными числовыми коэффициентами, то целесообразнее проанализировать критерии Гурвица с учетом этого необходимого условия. В результате такого анализа, излагаемого в большинстве руководств по теории автоматического управления [5], [6], можно получить систему неравенств, соблюдение которых эквивалентно выполнению условий устойчивости. Для систем первого и второго порядка необходимое условие устойчивости 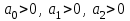 (16) (16)одновременно является и достаточным. Для систем более высокого порядка, кроме выполнения требования положительности всех коэффициентов характеристического уравнения, необходимо и достаточно соблюдение следующих неравенств: для систем третьего порядка 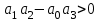 ; (17) ; (17) для системы четвертого порядка 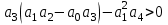 ; (18) ; (18) для системы пятого порядка 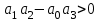 , ,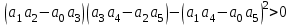 ; (19) ; (19) для системы шестого порядка 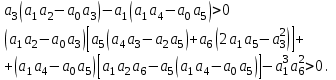 (20) (20) Оценить устойчивость САР по критерию Гурвица, если ее характеристическое уравнение имеет вид: 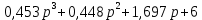 Для уравнения третьего порядка условием устойчивости по Гурвицу, помимо положительности коэффициентов уравнения: 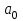 =0,453>0; =0,453>0; 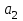 =1,697>0 =1,697>0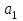 =0,448>0; =0,448>0; 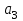 =6>0 =6>0является выполнение неравенства: 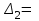 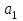 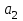 - - 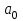 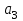  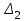 0,448*1,697-0,453*6=-1,95<0 0,448*1,697-0,453*6=-1,95<0Следовательно, система неустойчива. 3.3 Определение устойчивость по критерию Вышнеградского. Этот критерий используется при определений устойчивости системы, для которой характеристическое уравнение имеет третий порядок. В нашей системе третьего порядка: 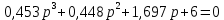 Уравнение необходимо преобразовать так, чтобы коэффициент при р3 был равен единице. Для этого разделим все члены характеристического уравнения на 0,17 и получим: 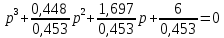 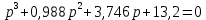 где 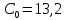 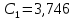 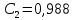 Находим величины Х и У: 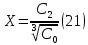 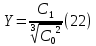 Подставляем значения: 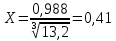 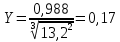 Отсюда получим: 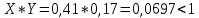 . .Вывод. Произведение ХУ 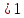 , следовательно АС неустойчива. , следовательно АС неустойчива. 4. Определение колебательного звена. Из значения динамических параметров ТДЗ напишем формулу колебательного звена: W (p)= 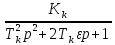 (23) (23)Из таблицы -1берем значения и подставляем в формулу (23). 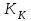 =1,7 =1,7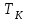 =4,2 =4,2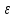 =0,5 =0,5Отсюда выводим: W(p)= 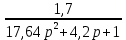 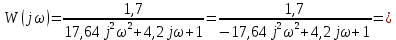 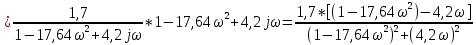 Отсюда 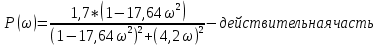 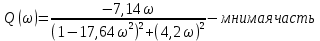 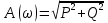 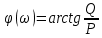 Таблица-5. Результаты расчета по колебательному звену
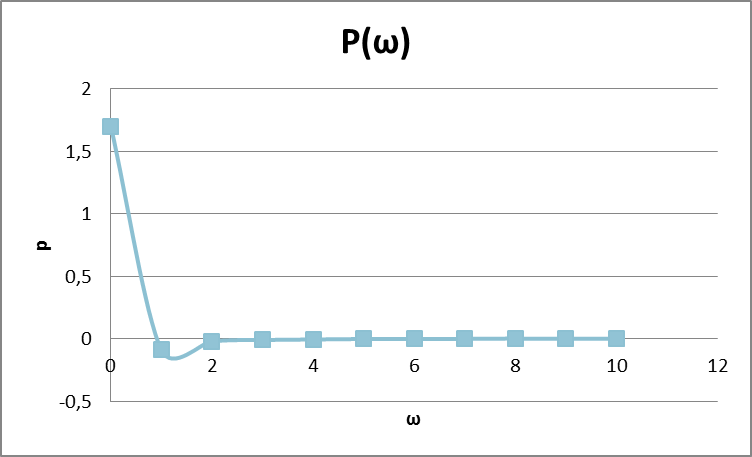 Рисунок – 10. Вещественная частотная характеристика 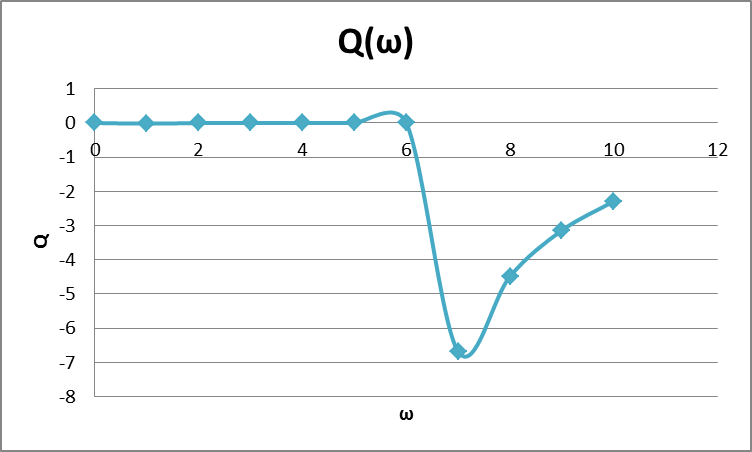 Рисунок – 11. Мнимая частотная характеристика 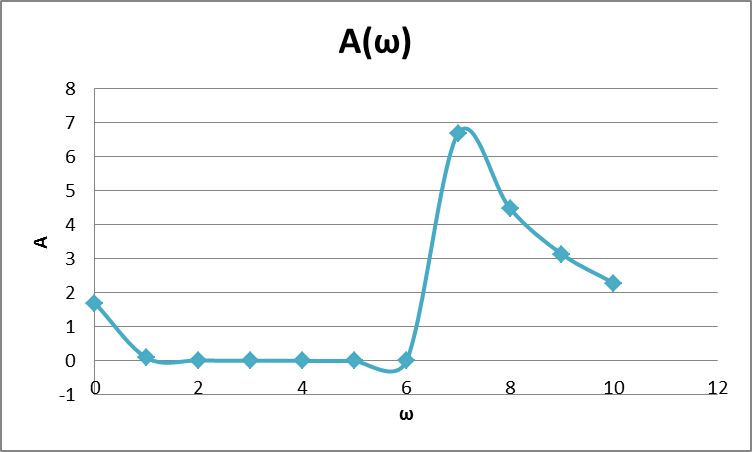 Рисунок – 12. Амплитудная частотная характеристика 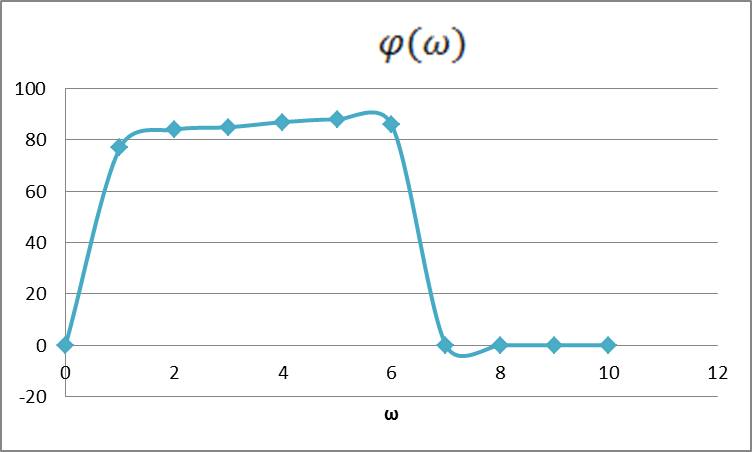 Рисунок – 13. Фазная частотная характеристика 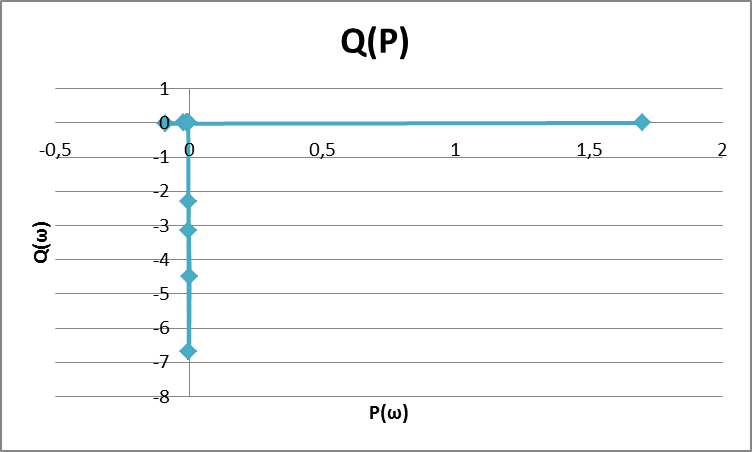 Рисунок – 14. Амплитудно – фазная частотная характеристика |