ТАу. Курсовая работа Фадеев П.А. ПС-33. Исследование асу на устойчивость работы по алгебраическим и частотным критериям
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
|
5. Расчет и построение частотных характеристик системы автоматического регулирования. Динамические параметры и структурная схема САР даны в таблицах 6 и 7. Для построения частотных характеристик САР необходимо выполнить те же этапы, которые даны в разделе 1.1, но уже применительно к системе и получить только требуемые в задании характеристики. Таблица-6. Структурная схема САР 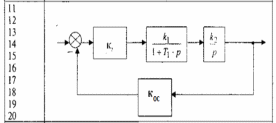 Таблица-7. Значения динамических параметров САР
Подставляя значения варианта -14, решаем задачу по структурной схеме 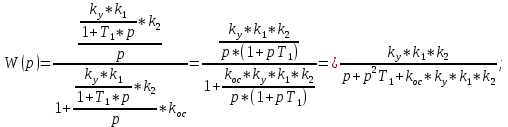 Подставим значения: 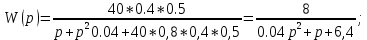 Для получения аналитических выражений ЧХ исследуемой системы производим формальную замену оператора Р на 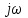 , тогда имеем , тогда имеем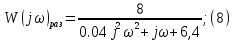 Умножим и разделим числитель и знаменатель на комплексное число, сопряженное знаменателю: 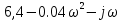 Отсюда получим: 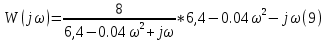 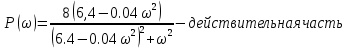 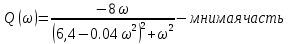 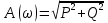 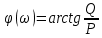 Таблица-8. Расчетные значения частотных характеристик САР
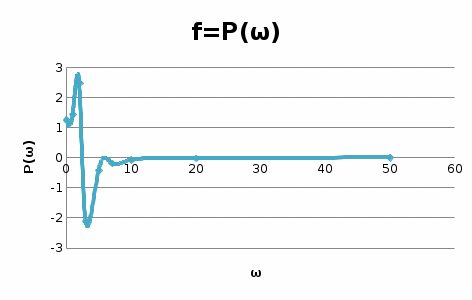 Рисунок – 16. Вещественная частотная характеристика 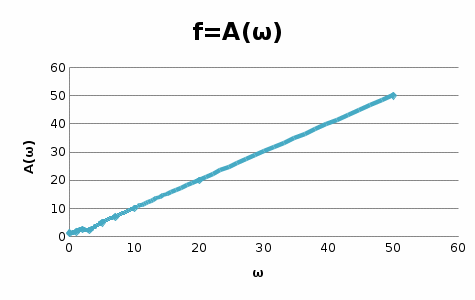 Рисунок – 17. Амплитудная частотная характеристика 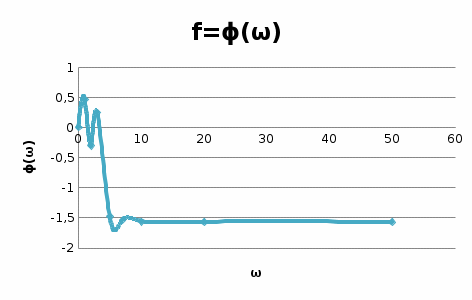 Рисунок – 18. Фазная частотная характеристика 6.Анализ устойчивости линейных систем . Для оценки устойчивости системы по алгебраическим критериям устойчивости Гурвица, Рауса необходимо выполнить следующие этапы: – определить передаточную функцию замкнутой системы; – полученную передаточную функцию упростить (привести к общему знаменателю, сократить, раскрыть скобки, привести подобные члены и расписать их по степени убывания оператора 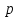 ) и получить ее в дробно – рациональном операторном виде; ) и получить ее в дробно – рациональном операторном виде;– выделить характеристическое уравнение системы; – оценить выполнение (невыполнение) необходимого условия устойчивости; – оценить выполнение (невыполнение) достаточного условия устойчивости, посчитав 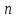 определителей Гурвица или таблицу – схему Рауса. определителей Гурвица или таблицу – схему Рауса.В случае использования критерия устойчивости Михайлова необходимо: – определить передаточную функцию замкнутой системы; – привести ее к дробно – рациональному виду и получить характеристическое уравнение системы; – в последнем произвести формальную замену оператора 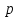 на на 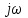 и выделить вещественную и мнимую части этого выражения; и выделить вещественную и мнимую части этого выражения;– задаваясь произвольно значениями 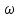 от 0 до от 0 до 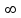 рассчитать значения рассчитать значения 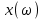 и и 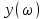 , полученные значения свести в таблицу. Рекомендуется посчитать , полученные значения свести в таблицу. Рекомендуется посчитатьпо 2 – 3 точки для каждого квадранта. – построить характеристическую кривую Михайлова (годограф) в плоскости 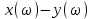 и дать оценку устойчивости системы. и дать оценку устойчивости системы.При оценке устойчивости системы по критерию Найквиста рекомендуется следующая последовательность: – определить передаточную функцию разомкнутой системы и привести ее к дробно – рациональному виду; – убедиться, что разомкнутая система является устойчивой, применив любой из известных критериев; – произвести формальную замену оператора 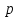 на на 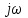 и выделить аналитические выражения вещественной и выделить аналитические выражения вещественной 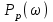 и мнимой – и мнимой – 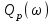 или амплитудной – или амплитудной – 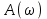 и фазовой и фазовой  характеристик разомкнутой системы; характеристик разомкнутой системы;– произвольно задаваясь фиксированными значениями круговой частоты 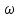 от 0 до от 0 до 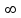 вычислить значения вычислить значения 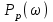 и и 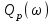 или или 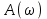 и и  , которые необходимо занести в таблицу; , которые необходимо занести в таблицу;– по расчетным данным построить АФЧХ разомкнутой системы и дать заключение об устойчивости замкнутой системы. Заключение В ходе выполнения курсовой работы была исследована система автоматического регулирования (САР) и был произведен расчет регулятора для данной системы по заданным показателям качества (показатель колебательности и время регулирования). Кроме того, были освоены методы коррекции неустойчивых систем для получения устойчивых при помощи последовательного включения звена коррекции. По критерий Гурвица, Раусса, Михайлова и Найквиста эффект действий дает возможность анализировать устойчивости систем. В систему были введены нелинейные элементы, и исследовано ее поведение при этом воздействии. Список использованной литературы. Тулегенов К.К., Джапарова Д.А. Методические указания по выполнению курсовой работы по дисциплине «Теория автоматического управления» по специальностям 5В071800-«Электроэнергетика», 5В071600-«Приборостроение» - Уральск, ЗКАТУ, 2013 . УМК ДС дисциплине Теория линейных систем автоматического регулрования. – Алматы, КазНТУ, 2008 . Бесекерский В.Л., Попов Е.П. Теория систем автоматического регулирования. - М.: Наука, 1977 г. Теория автоматического управления. Часть 1, 2. /Воронов А.А. - М.: Высшая школа, 1986. | ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||