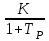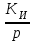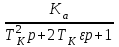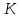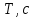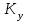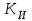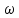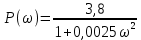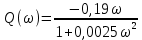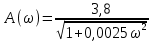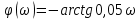ТАу. Курсовая работа Фадеев П.А. ПС-33. Исследование асу на устойчивость работы по алгебраическим и частотным критериям
 Скачать 0.5 Mb. Скачать 0.5 Mb.
|
 МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РЕСПУБЛИКИ КАЗАХСТАН. МИНИСТЕРСТВО СЕЛЬСКОГО ХОЗЯЙСТВА РЕСПУБЛИКИ КАЗАХСТАН.Западно-Казахстанский аграрно-технический университет имени Жангир хана. Кафедра «Высшая школа электротехники и автоматики» Курсовая работа. По дисциплине: «Теория автоматического управления». На тему: «Исследование АСУ на устойчивость работы по алгебраическим и частотным критериям». 14-вариант. Выполнил: Фадеев П.А. ПС-33. Проверила: Джапарова Д.А. Уральск 2020 г. Содержание Введение.................................................................................................................3 1. Основные понятия теории автоматического управления..............................4 2.Расчет и построение частотных характеристик типовых динамических звеньев и систем ....................................................................................................7 3. Расчет и построение частотных характеристик систем ..............................13 3.1 Определение устойчивость по критерию Михайлова.................................16 3.2 Определение устойчивость по критерию Гурвица......................................17 3.3 Определение устойчивость по критерию Вышнеградского........................20 4. Определение колебательного звена.................................................................22 5. Расчет и построение частотных характеристик системы автоматического регулирования……………………………………………………………............26 6. Анализ устойчивости линейных систем ........................................................30 Заключение.............................................................................................................31 Список литературы.………………………………………………..…………….32 Введение В настоящее время автоматические системы управления все больше проникают во все области промышленности. Если в качестве примера обратиться к нефтегазовой отрасли, то можно увидеть, насколько стремительно системы автоматического управления изменили сам процесс автоматизации . Для современных промышленных производств характерна интенсификация технологических процессов, масштабы производств значительно возросли, усложнились и сами производственные процессы. Эффективная организация производства на современном этапе невозможна без широкомасштабного использования автоматических систем управления. Теория автоматического управления (ТАУ) – это научная дисциплина, которая является частью технической кибернетики и общей теории управления. При этом в теории автоматического управления широко применяются такие разделы математики, как дифференциальные и разностные уравнения, линейная алгебра, матричное исчисление, теория вероятности. Необходимо понимать, что в данном курсе мы затрагиваем лишь самые основные понятия, серьезное же изучение теории автоматического управления невозможно без освоения соответствующего математического аппарата. Методы исследования, разработанные в теории автоматического управления (регулирования), являются довольно общими, область применения их выходит за рамки практического приложения дисциплины. Принципы автоматического управления (регулирования), на основе которых строятся технические системы, имеют универсальный характер. Аналогичные принципы, например, принцип обратной связи, заложены в регуляционные системы живых организмов, системы управления производством, обществом и т.д. Таким образом, изучение теории автоматического управление становится необходимым для широкого круга специалистов, работающих во всех областях современной промышленности. 1. Основные понятия теории автоматического управления. В теории автоматического управления принимаются следующие аргументы: Управление - разработка управляющих воздействий для перевода объекта управления в желаемое состояние. Автоматическое регулирование – поддержание постоянной определенной физической величины или изменение ее по определенному закону с помощью автоматических устройств. Следует отметить, что изменение закона может быть неизвестным ранее. Объектом регулирования (управления) ОП (ОУ) является машина, аппарат или агрегат, в котором осуществляется регулирование. Это может быть главный насосный агрегат, сепаратор, качалка, обрабатывающие баки и так далее. Регулируемые величины – это физическое количество, которое подлежит регулированию. Это может быть давление в трубопроводе, число оборотов вала двигателя, температура масла. В качестве примера рассмотрим уровень жидкости в технологическом резервуаре. Автоматический регулятор (АР) – это совокупность устройств, обеспечивающих процесс регулирования без вмешательства человека. Другими словами, АП получает информацию об объекте управления (или) и генерирует сигнал, который принадлежит этому объекту. 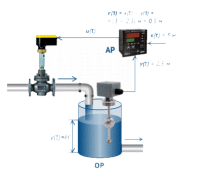 Основные понятия теории автоматического управления. Автоматический контроллер (регулятор) также получает конкретную задачу или задание действия x(t) – требуемое значение контролируемой цены, которое должен поддерживать контроллер. Пример этой функции соответствует 3 - метровому уровню жидкости. А объект управления с помощью датчиков, автоматических регуляторов получает цену контролируемого значения y(t). предположим, что в нашем случае фактическое значение уровня жидкости измеряется с помощью уровнемера 2,5 метра. Автоматический регулятор определяет ошибку управления (было за несоответствие) – разницу между заданным и фактическим значениями в контрольной цене. В нашем случае эта погрешность составит 0,5 метра. Эта ошибка может меняться с течением времени. обозначим как e(t). Почему же за несовпадение времени произошло изменение? Различные возмущающие элементы на самом деле в объекте регулирования. Возмущение (возмущение) f (t) – любое внешнее воздействие на объект, являющееся причиной злостного отклонения контролируемого значения от заданного значения. Например, в рассматриваемом случае такими возмущающими эффектами могут быть изменение объема отбора проб из резервуара или, наоборот, выпадение осадков, которые приводят к повышению уровня жидкости. Автоматический регулятор, имеющий определенную погрешность управления, генерирует управляющее (суждение) воздействие u (t) для компенсации действия путаницы. Это управляющее воздействие передается, как и в обычном непосредственном объекте, регулирующим органом. В нашем случае это регулируемый клапан с электроприводом. Совокупность объекта регулирования (управления) и регулятора называется системой автоматического регулирования (АСР). AR, и OR обычно представлены упрощенно в виде функциональных диаграмм. Для изображения каждого из элементов и связей в теории автоматического управления используются специальные символы, где связи между элементами представлены стрелками, сами элементы, следовательно, пояснительными надписями, а элементы, в которых сравниваются несколько эталонов, представлены сумматорами. Более того, по внешнему виду такого сумматора можно судить о том, что математическая операция им завершена. В качестве примера в системе сравнения между фактическим уровнем жидкости в баке и заданием будет показан символ из третьей строки таблицы.
В САУ данные подаются по замкнутому контуру: датчики получают информацию, передают ее на контроллер, контроллер выдает управляющий сигнал водителям, которые действуют непосредственно на объект; поэтому данные об обновленном состоянии объекта датчиками возвращаются на контроллер, и цикл повторяется.  РЕГУЛЯТОР     ПРИВОДЫ ДАТЧИКИ    ОБЬЕКТ УПРАВЛЕНИЯ Основная схема регулирования (управления) 2. Расчет и построение частотных характеристик типовых динамических звеньев. Частотные характеристики 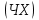 получили широкое использование при анализе и синтезе систем автоматического регулирования (САР). Выражения для частотных характеристик типовых динамических звеньев (ТДЗ) и систем могут быть получены из передаточных функций (ПФ), написанных в операторной форме, путем формальной замены оператора p на получили широкое использование при анализе и синтезе систем автоматического регулирования (САР). Выражения для частотных характеристик типовых динамических звеньев (ТДЗ) и систем могут быть получены из передаточных функций (ПФ), написанных в операторной форме, путем формальной замены оператора p на 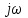 . .Физически ЧХ замкнутой или разомкнутой САР имеет место при подаче на вход ТДЗ или системы гармонического воздействия при изменении частоты 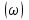 от нуля до бесконечности и сохранения постоянной амплитуды входного сигнала на всем диапазоне изменения частот. от нуля до бесконечности и сохранения постоянной амплитуды входного сигнала на всем диапазоне изменения частот.При подаче на вход линейного ТДЗ или САР гармонического воздействия 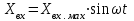 (1) (1)характеристика отработки по окончании переходного процесса будет также представлять собой периодическую функцию вида 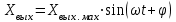 (2) (2)отличающуюся от входной функции по амплитуде и по фазе, но имеющую ту же частоту, что и входная функция. При этом ТДЗ или САР будет находиться в режиме вынужденных колебаний [2]. Отношение 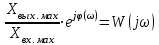 (3) (3) представляет собой комплексную частотную функцию, которая называется комплексным коэффициентом усиления ТДЗ или САР. Таким образом, выходная величина определяется произведением входной величины на комплексную частотную функцию, которая может быть непосредственно получена из ПФ, т.е. 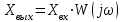 (4) (4)Выражение для 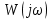 может быть разделено на вещественную и мнимую части может быть разделено на вещественную и мнимую части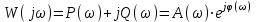 (5) (5)где 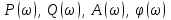 - полиномы от - полиномы от 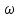 . .При изменении частоты 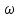 амплитуда и фаза амплитуда и фаза 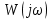 будут изменяться, а их конец будет описывать на плоскости комплексного переменного кривую, представляющую собой амплитудно-фазовую частотную характеристику (АФЧХ) ТДЗ или замкнутой САР. будут изменяться, а их конец будет описывать на плоскости комплексного переменного кривую, представляющую собой амплитудно-фазовую частотную характеристику (АФЧХ) ТДЗ или замкнутой САР. Таблица. Значения динамических параметров ТДЗ варианта №14.
Очевидно, что при изменении частоты будут изменяться также величины 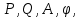 что позволяет построить ЧХ и для этих величин. что позволяет построить ЧХ и для этих величин. Соответственно имеются: 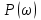 – вещественная частотная характеристика (ВЧХ); – вещественная частотная характеристика (ВЧХ);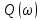 – мнимая частотная характеристика (МЧХ); – мнимая частотная характеристика (МЧХ);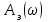 – амплитудная частотная характеристика (АЧХ); – амплитудная частотная характеристика (АЧХ);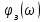 – фазовая частотная характеристика (ФЧХ). – фазовая частотная характеристика (ФЧХ).Соотношения между характеристиками определяются выражениями 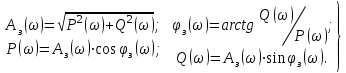 (6) (6)Подобные характеристики могут быть получены как для замкнутой системы, так и разомкнутой, а также для ТДВ. Ценность использования ЧХ заключается в том, что они позволяют косвенно, т.е. без решения дифференциального уравнения системы, судить о поведении последней в отношении устойчивости и ряда показателей качества, а также определять средства коррекции системы для получения заданных динамических показателей. По варианту -9 построить ЧХ инерционного звена, если ее ПФ имеет вид 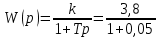 Определим аналитические выражения для всех ЧХ этого звена. Для этого произведем формальную замену оператора Лапласа 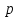 на на 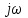 в заданной ПФ. в заданной ПФ. Тогда 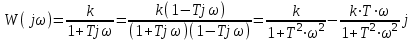 . (7) . (7)Из последнего выражения имеем 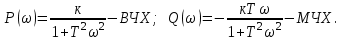 Используя выражение (6), получим 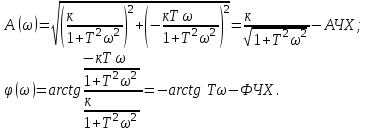 Произведем расчет ЧХ по полученным выше их аналитическим выражениям и результаты расчета сведем в таблицу 1, предварительно подставив в эти выражения заданные численные значения динамических параметров: К=3,8 и T=0,05 с Таблица 2 – Расчетные значения ЧХ инерционного звена
Графики рассчитанных ЧХ инерционного звена показаны на рисунках 1, 2,3, 4, 5. Построение АФЧХ инерционного звена можно произвести по расчетным значениям 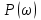 и и 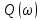 в декартовых координатах или в полярных координатах по значениям в декартовых координатах или в полярных координатах по значениям 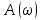 и и  . .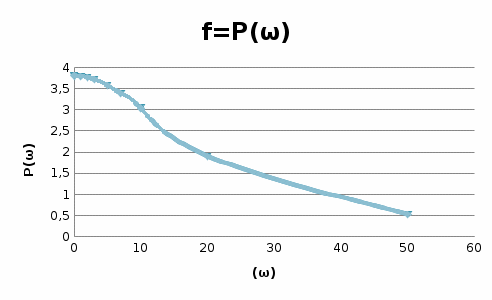 Рисунок 1 – ВЧХ инерционного звена 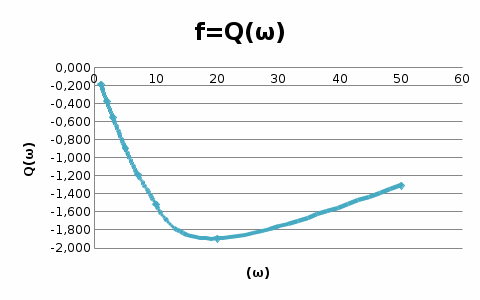 Рисунок 2 – МЧХ инерционного звена 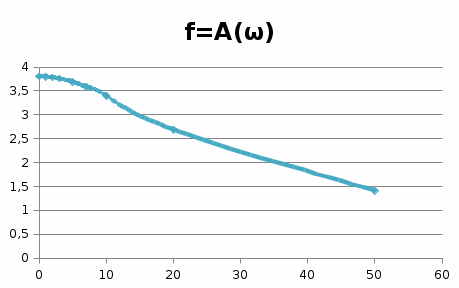 Рисунок 3 – АЧХ инерционного звена масштаба ( 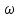 ) )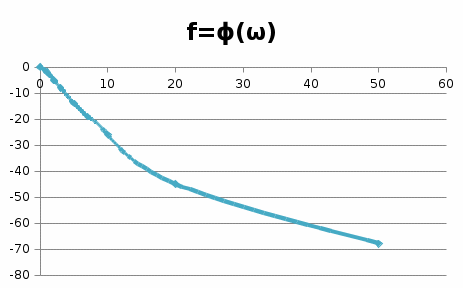 Рисунок 4 – ФЧХ инерционного звена 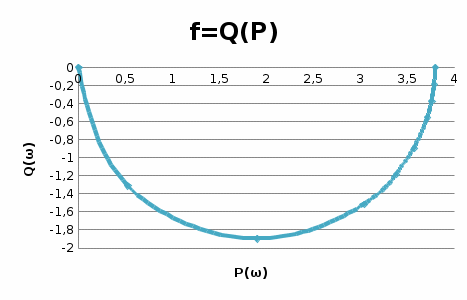 Рисунок 5 – АФЧХ инерционного звена, построенная по данным 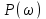 и и 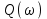 В аналогичный последовательности строятся ЧХ всех остальных ТДЗ. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||










 a
a