лабораторна работа н 3. Лабораторная работа N 3 группы 0283 Абдукахоров Оятулло. Исследование динамики колебательного и вращательного движения
 Скачать 0.66 Mb. Скачать 0.66 Mb.
|
|
Отчет По лабораторной работе No 3 по дисциплине ,,Физика ‘’ Тема:,, Исследование динамики колебательного и вращательного движения‘’ Студент группы 0283 Абдукахоров О А Предподователь Попов Ю И Цель работы. Исследование динамики колебательного движения на примере крутильного маятника, определение момента инерции маятника, модуля сдвига материала его подвеса и характеристик колебательной системы с затуханием (логарифмического декремента затухания и добротности колебательной системы ) Приборы и принадлежности. Крутильный маятник, секундомер, масштабная линейка, микрометр. Применяемый в работе крутильный маятник, представляет собой диск 1, закрепленный на упругой стальной проволоке 2, свободный крнец который зажат в неподвижном кронштейне 3 на кронштейне расположено кольцо 4, масса которого известна. Кольцо 4 можно положить сверху на диск 1, изменив тем самым момент инерции маятника. Для отчета значений угла поворота маятника служит градуированная шкала 5, помешенная на панели прибора снизу от диска 1 . Исследуемые закономерности Исследуемые закономерности Крутильный маятник. При повороте тела, закрепленного на упругом подвесе, в результате деформации сдвига при закручивании подвеса возникает возвращающий момент упругих сил M = k, где k - коэффициент кручения, зависящий от упругих свойств материала подвеса, его размеров и формы, - угол поворота. При малых углах поворота, без учета сил трения в подвесе, крутильные колебания маятника являются гармоническими, а уравнение движения тела имеет вид
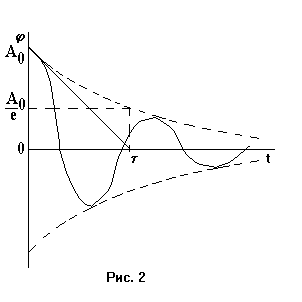
и является уравнением движения осциллятора с затуханием. Колебания такого осциллятора уже не будут гармоническими. Коэффициент = R/2I называют коэффициентом затухания. Если 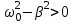 , движение крутильного маятника описывается уравнением затухающих колебаний , движение крутильного маятника описывается уравнением затухающих колебаний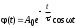 , ,где 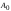 - начальная амплитуда колебаний маятника, = 1/ - время затухания, определяющее скорость убывания амплитуды A(t) маятника, численно равное времени, за которое амплитуда убывает в e раз (рис. 2), т.е. - начальная амплитуда колебаний маятника, = 1/ - время затухания, определяющее скорость убывания амплитуды A(t) маятника, численно равное времени, за которое амплитуда убывает в e раз (рис. 2), т.е.
Крутильный маятник как диссипативная система Полная энергия колебаний маятника убывает со временем по закону 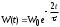 , ,где 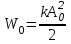 - начальная энергия колебаний. - начальная энергия колебаний. Убывание энергии происходит за счет совершения работы против сил трения. Энергия при этом превращается в тепло, идет процесс диссипации энергии. Скорость диссипации энергии (мощность потерь) 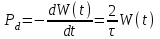 . . Помимо коэффициента затухания (или времени затухания ) и мощности потерь Pdколебательная диссипативная система характеризуется также добротностью Q , позволяющей судить о способности системы сохранять энергию. Добротность определяется отношением запасенной системой энергии к потерям энергии за время T/2 = 1/. Легко видеть, что добротность 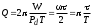 , ,т.е. численно равна числу колебаний за время t = . За это время амплитуда колебаний уменьшается в e 23 раза, а энергия колебаний в e2 535 раз, иными словами, за это время колебания практически затухают. В технике для характеристики колебательных систем с затуханием вводят декремент затухания (), или его логарифм – логарифмический декремент затухания ( = ln), определяя эти параметры через отношение амплитуд колебаний, соответствующих соседним периодам 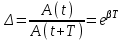 или = T. или = T.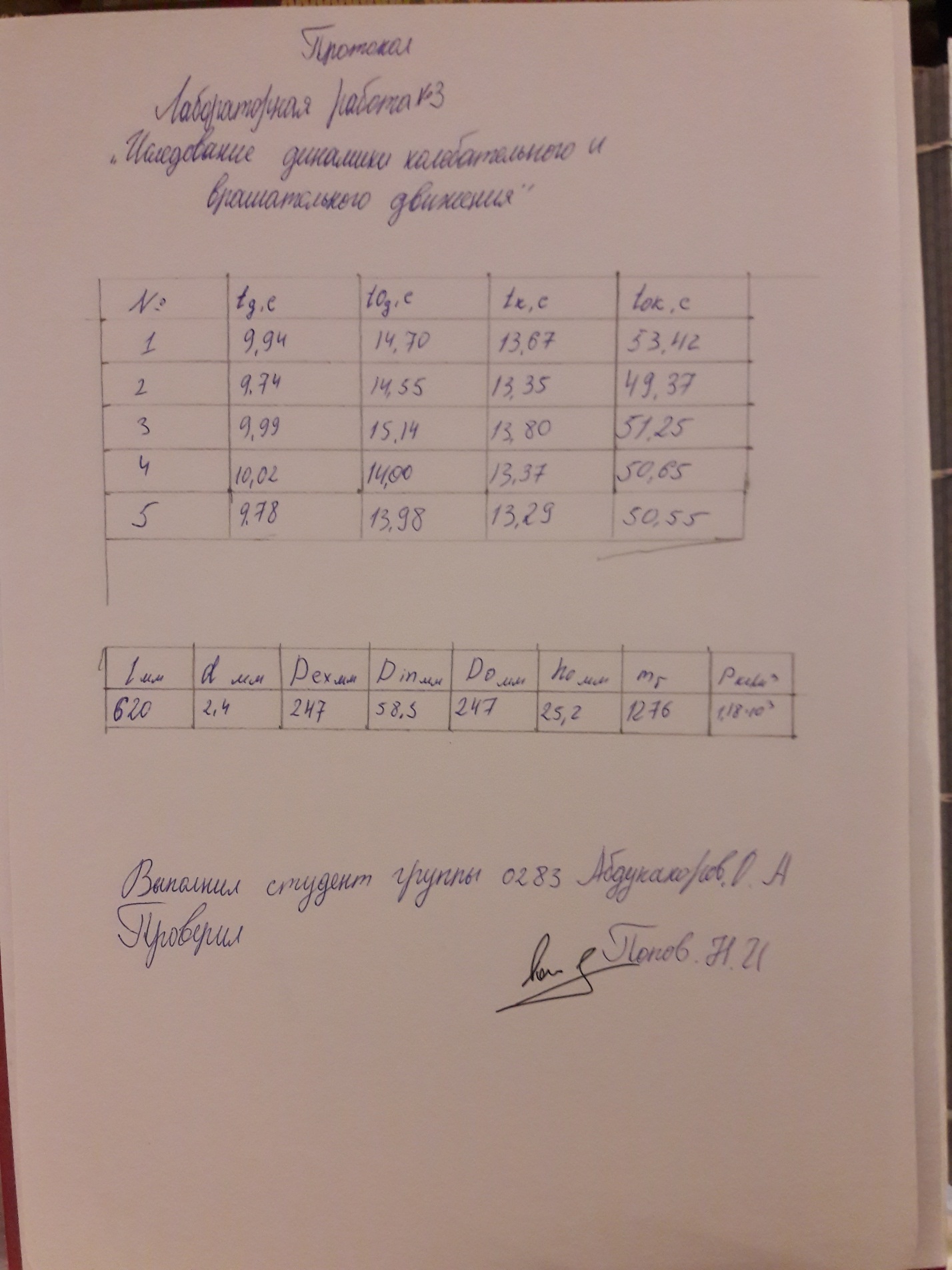 ОБРАБОТКА РЕЗУЛЬТАТОВ   |

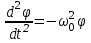 ,
,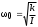 ,
,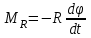 ,
,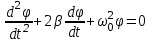
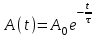 при t =
при t = 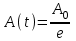 ,
,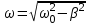 .
. 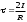 .
.