ЛАбаа по физике 1. ЛАБАПОФИЗИКЕ1. Исследование движения тел
 Скачать 290.06 Kb. Скачать 290.06 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра Физики отчет по лабораторной работе №1 по дисциплине «Физике» Тема: ИССЛЕДОВАНИЕ ДВИЖЕНИЯ ТЕЛ
В ДИССИПАТИВНОЙ СРЕДЕ
Санкт-Петербург, 2022 Цель работы. Определение вязкости диссипативной среды (жидкости) по установившейся скорости движения шарика в ней, а также исследование процессов рассеяния энергии в диссипативной среде. Основные теоретические положения. Приборы и принадлежности: цилиндрический сосуд с жидкостью, металлические шарики, аналитические весы, масштабная линейка, секундомер.  В работе используется цилиндрический сосуд (рис. 1.1), на боковой поверхности которого нанесены метки. Измеряя расстояние между метками и время движения шарика в жидкости между ними, можно определить скорость его падения. Шарик опускается в жидкость через впускной патрубок, расположенный в крышке цилиндра. В работе используется цилиндрический сосуд (рис. 1.1), на боковой поверхности которого нанесены метки. Измеряя расстояние между метками и время движения шарика в жидкости между ними, можно определить скорость его падения. Шарик опускается в жидкость через впускной патрубок, расположенный в крышке цилиндра.Исследуемые закономерности: В  язкость (внутреннее трение) жидкостей и газов выражается в свойстве оказывать сопротивление перемещению их слоев друг относительно друга и возникновении сил трения между слоями жидкости или газа, перемещающимися с различной скоростью. При достаточно высокой вязкости жидкости и малых скоростях движения слоев они движутся практически параллельно друг другу (ламинарное течение) в направлении оси Ox с разной скоростью язкость (внутреннее трение) жидкостей и газов выражается в свойстве оказывать сопротивление перемещению их слоев друг относительно друга и возникновении сил трения между слоями жидкости или газа, перемещающимися с различной скоростью. При достаточно высокой вязкости жидкости и малых скоростях движения слоев они движутся практически параллельно друг другу (ламинарное течение) в направлении оси Ox с разной скоростью Сила трения направлена по касательной к поверхности соприкосновения слоев и описывается законом Ньютона 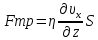 , где , где  -производная скорости по нормали к слоям, S – площадь соприкосновения слоев, – коэффициент внутреннего трения (динамическая вязкость). Величина обратная вязкости 1/ называется текучестью. Наряду с динамической вязкостью часто используется кинематическая вязкость / , где – плотность жидкости. -производная скорости по нормали к слоям, S – площадь соприкосновения слоев, – коэффициент внутреннего трения (динамическая вязкость). Величина обратная вязкости 1/ называется текучестью. Наряду с динамической вязкостью часто используется кинематическая вязкость / , где – плотность жидкости.Внутреннее трение в газах определяется переносом импульса при переходе молекул из одного слоя газа в другой. На движение молекул в жидкости, в отличие от газа, сильно влияет межмолекулярное взаимодействие, ограничивающее их подвижность. Молекула жидкости большую часть времени совершает колебания около положения равновесия внутри небольшого объема. Поэтому во внутреннее трение в жидкости дополнительный вклад дает взаимодействие между молекулами слоев жидкости. Как следствие, вязкость жидкостей в очень сильной степени зависит от температуры. С ростом температуры подвижность молекул жидкости возрастает, а вязкость падает, т.к. с увеличением температуры тепловое движение молекул усиливается, а среднее время “оседлой жизни” молекулы (время релаксации) уменьшается. При н 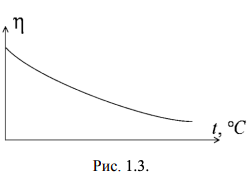 евысоких температурах коэффициент динамической вязкости изменяется по закону евысоких температурах коэффициент динамической вязкости изменяется по закону  , где k – постоянная Больцмана, T – абсолютная температура, E – энергия, которую должна приобрести молекула, чтобы перейти от одного положения к другому (энергия активации). Характерный вид температурной зависимости вязкости изображен на рис. 1.3. , где k – постоянная Больцмана, T – абсолютная температура, E – энергия, которую должна приобрести молекула, чтобы перейти от одного положения к другому (энергия активации). Характерный вид температурной зависимости вязкости изображен на рис. 1.3. Сила сопротивления движению тела в вязкой среде. В вязкой среде на движущееся тело действует сила сопротивления, направленная противоположно скорости тела. При небольших скоростях и небольших размерах тела эта сила обусловлена вязким трением между слоями среды и пропорциональна скорости тела 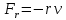 , где v – скорость движения тела, r – коэффициент сопротивления, зависящий от формы, размеров тела и от вязкости среды . , где v – скорость движения тела, r – коэффициент сопротивления, зависящий от формы, размеров тела и от вязкости среды . Для шара радиуса R коэффициент сопротивления определяется формулой Стокса  . . П  ри движении тела в вязкой среде происходит рассеяние (диссипация) его кинетической энергии. Слои жидкости, находящиеся на разном расстоянии от движущегося тела, имеют различную скорость. Слой жидкости, находящийся в непосредственной близости от поверхности движущегося тела, имеет ту же скорость, что и тело, по мере удаления от него скорость слоев жидкости плавно уменьшается, рис. 1.4. В этом состоит явление вязкого трения, в результате которого движения тела передается слоям окружающей среды в направлении, перпендикулярном движению тела. Если скорость тела велика или тело имеет большие размеры, за телом возникают вихри и обтекание становится турбулентным. В этом случае сила сопротивления становится пропорциональной квадрату скорости: ри движении тела в вязкой среде происходит рассеяние (диссипация) его кинетической энергии. Слои жидкости, находящиеся на разном расстоянии от движущегося тела, имеют различную скорость. Слой жидкости, находящийся в непосредственной близости от поверхности движущегося тела, имеет ту же скорость, что и тело, по мере удаления от него скорость слоев жидкости плавно уменьшается, рис. 1.4. В этом состоит явление вязкого трения, в результате которого движения тела передается слоям окружающей среды в направлении, перпендикулярном движению тела. Если скорость тела велика или тело имеет большие размеры, за телом возникают вихри и обтекание становится турбулентным. В этом случае сила сопротивления становится пропорциональной квадрату скорости: 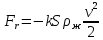 , где S – площадь поперечного сечения тела, а , где S – площадь поперечного сечения тела, а 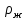 – плотность жидкости, k – коэффициент пропорциональности. Сила сопротивления при турбулентном обтекании определяется не столько трением одних слоев жидкости о другие, сколько увеличением кинетической энергии жидкости, вынужденной двигаться, чтобы расступиться и пропустить тело. – плотность жидкости, k – коэффициент пропорциональности. Сила сопротивления при турбулентном обтекании определяется не столько трением одних слоев жидкости о другие, сколько увеличением кинетической энергии жидкости, вынужденной двигаться, чтобы расступиться и пропустить тело. Критерием характера движения слоев жидкости (ламинарного или турбулентного) при падении в ней шарика радиуса R со скоростью  является число Рейнольдса является число Рейнольдса 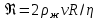 . При Re<2300 движение слоев – ламинарное, при Re>2300- турбулентное. . При Re<2300 движение слоев – ламинарное, при Re>2300- турбулентное. Движение тела в диссипативной среде. Рассмотрим падение шарика в жидкости. В исследуемом в лабораторной работе случае скорость падения шарика невелика, и можно считать, что сила сопротивления пропорциональна первой степени его скорости. Пусть начальная скорость шарика у поверхности жидкости 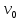 , его радиус R , а , его радиус R , а 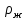 и и 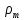 – плотности жидкости и шарика соответственно. – плотности жидкости и шарика соответственно. Согласно II закону Ньютона:  . . Здесь 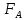 – сила Архимеда, – сила Архимеда, – сила Стокса, Fmg – сила Стокса, Fmg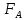 =m(1- =m(1-  )g-движущая сила, m –присоединенная масса жидкости, увлекаемая телом за собой. Присоединённой массой называется такая фиктивная масса жидкости, кинетическая энергия которой при ее движении со скоростью тела равна кинетической̆ энергии окружающей̆ тело жидкости. Присоединенная масса зависит от размеров и формы погруженной в жидкость части тела. Для шарика присоединенная масса равна половине массы вытесненной жидкости: )g-движущая сила, m –присоединенная масса жидкости, увлекаемая телом за собой. Присоединённой массой называется такая фиктивная масса жидкости, кинетическая энергия которой при ее движении со скоростью тела равна кинетической̆ энергии окружающей̆ тело жидкости. Присоединенная масса зависит от размеров и формы погруженной в жидкость части тела. Для шарика присоединенная масса равна половине массы вытесненной жидкости: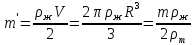 , откуда , откуда 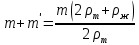 , ,  . Если ввести обозначения . Если ввести обозначения 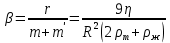 , , 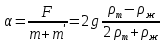 , то задача сведется к решению неоднородного дифференциального уравнения вида , то задача сведется к решению неоднородного дифференциального уравнения вида  . .Данное уравнение имеет решение:  , , 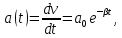 где где  скорость падения шарика на поверхность жидкости или его начальная скорость, скорость падения шарика на поверхность жидкости или его начальная скорость,  - установившаяся скорость движения шарика, - установившаяся скорость движения шарика, 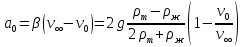 - его начальное ускорение. - его начальное ускорение.З  ависимость скорости движения тела в диссипативной среде от времени представлена на рис. 1.5. Видно, что скорость шарика в зависимости от величины начальной скорости может либо убывать, при ависимость скорости движения тела в диссипативной среде от времени представлена на рис. 1.5. Видно, что скорость шарика в зависимости от величины начальной скорости может либо убывать, при 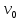 / , либо возрастать при 0 / , либо возрастать при 0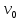 / v, но в любом случае асимптотически стремится к постоянному значению / v, но в любом случае асимптотически стремится к постоянному значению  . . Время, за которое величина ускорения по отношению к своему начальному значению  изменяется в e раз или отклонение скорости тела от равновесной скорости изменяется в e раз или отклонение скорости тела от равновесной скорости  по отношению к своему начальному значению по отношению к своему начальному значению 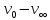 изменяется в e раз называется временем релаксации процесса перехода движения тела от нестационарного режима к стационарному. Его также можно найти как изменяется в e раз называется временем релаксации процесса перехода движения тела от нестационарного режима к стационарному. Его также можно найти как 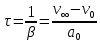 . В исследуемом случае характерное значение составляет доли секунды. Время движения шарика до первой метки многократно превышает , и движение шарика между метками можно считать равномерным, а значение его установившейся скорости находить как . В исследуемом случае характерное значение составляет доли секунды. Время движения шарика до первой метки многократно превышает , и движение шарика между метками можно считать равномерным, а значение его установившейся скорости находить как 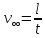 , где l расстояние между метками. , где l расстояние между метками. Второй закон Ньютона в случае стационарного движения шарика имеет вид 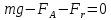 или или 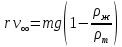 Из полученного уравнения может быть найден коэффициент сопротивления среды:  , а по формуле Стокса–Эйнштейна – вязкость среды: , а по формуле Стокса–Эйнштейна – вязкость среды:  . .Радиус шарика может быть выражен через его массу 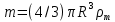 , , Тогда 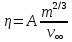 , где А – константа, зависящая от плотности жидкости и материала шарика: , где А – константа, зависящая от плотности жидкости и материала шарика:  . .В лабораторной работе в качестве жидкости используется глицериновое масло, его плотность  , материал шарика – свинец, , материал шарика – свинец, 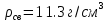 или сталь или сталь  . .Превращение энергии в диссипативной системе. Полная механическая энергия движущегося в жидкости тела в произвольный момент времени определяется выражением  , где h – высота расположения тела над дном сосуда. , где h – высота расположения тела над дном сосуда. В установившемся режиме 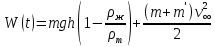 . .Передача энергии жидкой среде, окружающей движущееся тело, происходит за счет совершения работы против сил трения. Энергия при этом превращается в тепло. Скорость диссипации энергии (мощность потерь) в установившемся режиме может быть найдена как 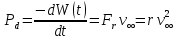 . .Уравнение баланса энергии на участке установившегося движения имеет вид: 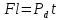 , или , или 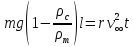 , где l = , где l =  – путь, проходимый телом между двумя метками, за время t. Уравнения движения тела (второй закон Ньютона) и баланса энергии при установившемся движении тела эквивалентны друг другу. – путь, проходимый телом между двумя метками, за время t. Уравнения движения тела (второй закон Ньютона) и баланса энергии при установившемся движении тела эквивалентны друг другу.Обработка результатов эксперимента: Расчёт значения коэффициента A:  . . . .Определим значения скорости и вязкости:   Па*с Па*с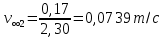  Па*с Па*с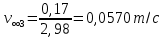  Па*с Па*с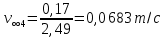  Па*с Па*с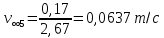  Па*с Па*с
Измерение под номером 3 при проверке оказалось промахом. Таблица 1.4 Новые сводные значения
7. Сравним экспериментальное значение вязкости с табличным Табличные значения: 0.26 Па*с Экспериментальные значения: 0,49 ± 0,06 Вывод: Коэффициент вязкости ( Сводная таблица: 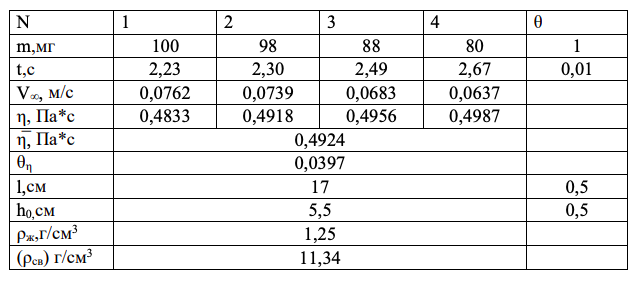 Коэффициент вязкости отличается от стандартных значений из-за погрешностей. Такой погрешностью может быть округление данных, неточности приборов и то, что не была учтена температура в формуле вязкости тела, поэтому расчётное значение вязкости получилось для температуры больше, чем фактическая по результатам измерений Коэффициент вязкости отличается от стандартных значений из-за погрешностей. Такой погрешностью может быть округление данных, неточности приборов и то, что не была учтена температура в формуле вязкости тела, поэтому расчётное значение вязкости получилось для температуры больше, чем фактическая по результатам измерений Ответы на вопросы: Таким образом, диссипативными характеристиками элементов системы являются коэффициент сопротивления b и коэффициент рассеивания. Они характеризуют диссипацию энергии в колебательной системе, происходящую за счет контактного и внутреннего трения в элементах и сопряжениях, обладающих упруго-диссипативными свойствами. При небольших скоростях (существенно меньших скорости распространения звуковых волн в данной среде) эта сила обусловлена вязким трением между слоями среды и пропорциональна скорости тела, где v– скорость движения тела, r– коэффициент сопротивления, зависящий от формы, размеров тела и от вязкости среды h. Для шара радиуса. R коэффициент сопротивления определяется формулой Стокса. Кинематическая вязкость определяется как отношение динамической вязкости к плотности среды и характеризует текучесть жидкости и зависит от ее плотности. А динамическая вязкость характеризует сопротивляемость жидкости силе, заставляющей ее течь. Qтр = Aтр = Fтр*s Нужно силу трения умножить на пройденный путь (расстояние).  | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

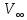 , m/c
, m/c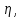 Па*c
Па*c Па*c
Па*c