Главная страница
Навигация по странице:

  • Выполнение работы: Задание 1.

  • Задание 2.

  • Вывод

    		•

    Лабораторная работа. Определение коэффициента вязкости жидкости методом Стокса. Лабораторная работа 13. Определение коэффициента вязкости жидкости по методу Стокса


    Скачать 469.66 Kb.
    НазваниеЛабораторная работа 13. Определение коэффициента вязкости жидкости по методу Стокса
    АнкорЛабораторная работа
    Дата26.10.2022
    Размер469.66 Kb.
    Формат файлаdocx
    Имя файлаОпределение коэффициента вязкости жидкости методом Стокса.docx
    ТипЛабораторная работа
    #755453


    Лабораторная работа 13.
    «Определение коэффициента вязкости жидкости по методу Стокса»

    Цель работы изучение явления внутреннего трения в жидкости и

    измерение коэффициента вязкости жидкости по скорости

    падения в ней шарика.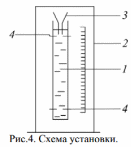



    Для проведения опыта используют цилиндрический стеклянный сосуд, заполненный глицерином или любой другой жидкостью с явно выраженными свойствами вязкости, шарики малых размеров, микрометр, масштабную линейку с миллиметровыми делениями, пинцет, термометр. Схема установки представлена на рис. 4.

    Выполнение работы:

    Задание 1. Определение коэффициента вязкости жидкости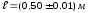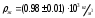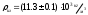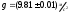









    Таблица1

    i
    1
    2
    3
    4
    5
    6
    7

    r, м
    0,0017
    0,0015
    0,0014
    0,0018
    0,0016
    0,0015
    0,0017

    r2, м2
    0,00000289
    0,00000225
    0,00000196
    0,00000324
    0,00000256
    0,00000225
    0,00000289

    t, c
    28,5
    29,3
    32,2
    28,2
    30,4
    29,7
    28,8

    t2, c2
    812,25
    858,49
    973,44
    1036,84
    924,16
    882,09
    829,44

    Вычислите средние значения

    =0,0016

    2>=0,0000026

    =29,67

    2>=880,4

    S<t>=0,01 c

    S<r>=0,001 м

    Рассчитайте среднее значение коэффициента вязкости жидкости: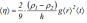



    <ŋ>=0,740 Па*с

    Рассчитайте среднеквадратичную погрешность определения <ŋ>: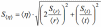



    S<ŋ>=0,003 Па*с

    Окончательный результат представьте в виде:

    <ŋ>=0,740±0,003 Па*с

    Используя формулу(4) определите число Рейнольдса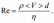



    Re=0,06

    Задание 2. Определение коэффициента вязкости жидкости из зависимости времени падения шарика t от 1/r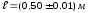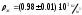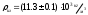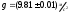









    Таблица2

    i
    1
    2
    3
    4
    5
    6
    7

    r, м
    0,0017
    0,0015
    0,0014
    0,0018
    0,0016
    0,0015
    0,0017

    Y=t, c
    28,5
    29,3
    32,2
    28,2
    30,4
    29,7
    28,8

    X=1/r2, 105 м-2
    3,46
    4,44
    5,1
    3,1
    3,9
    4,44
    3,46

    Постройте график зависимости t от 1/r2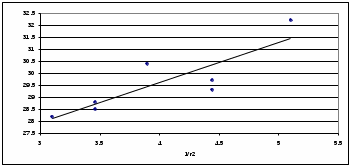

    .

    Из графика определите угловой коэффициент B.

    B= 3,3/2=1,65

    По найденному значению B рассчитайте среднее значение коэффициента вязкости жидкости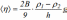



    <ŋ>=0,741 Па*с

    Б. Аналитический метод

    По формуле(17) определить угловой коэффициентB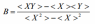



    B= 3,2/2=1,6

    По формуле(18) определить среднеквадратичного отклонения величины B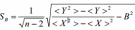



    SB=0,003

    Результат представьте в виде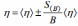



    <ŋ>=0,741±0,001 Па*с

    Используя формулу(4) определите число Рейнольдса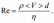



    Re=0,06

    Вывод: изучили явления внутреннего трения в жидкостях и опытным путем определение величины коэффициента вязкости жидкости методом Стокса.

    Контрольные вопросы

    1. Силы внутреннего трения и их природа? От каких факторов зависит коэффициент динамической вязкости?

    При движении жидкости между слоями возникают силы внутреннего трения, которые стремятся уровнять скорости всех слоев жидкости.

    Коэффициент вязкости является одной из важнейших характеристик смазочных материалов. Вязкость зависит от температуры, причем характер этой зависимости для жидкостей с увеличением температуры уменьшается.

    2. Напишите формулу Ньютона для сил внутреннего трения. Поясните понятие градиента скорости течения жидкости с помощью рисунка.



    3. Объясните метод Стокса определения вязкости жидкости и дайте вывод формулы(12).







    4. Как различаются течения ламинарное и турбулентное.

    Течение называется ламинарным(слоистым), если вдоль потока каждый выделенный тонкий слой скользит относительно соседних, не перемешиваясь с ними, и турбулентным (вихревым), если вдоль потока происходит интенсивное вихреобразование и перемешивание жидкости(газа). Ламинарное течение жидкости наблюдается при небольших скоростях ее движения. При турбулентном течении частицы жидкости приобретают составляющие скоростей, перпендикулярные течению, поэтому они могут переходить из одного слоя в другой. Скорость частиц жидкости быстро возрастает по мере удаления от поверхности трубы,

    затем изменяется довольно незначительно.

    написать администратору сайта