Исследование электронного парамагнитного резонанса (эпр) в слабом магнитном поле
 Скачать 109.35 Kb.
|
| ||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| Вопросы | Задачи ИДЗ | Даты коллоквиума | Итог | |||||||
| | | | | | | | | | ||
| | | | | | | | | | ||
| | ||||||||||
| | ||||||||||
| | ||||||||||
| | ||||||||||
Санкт-Петербург, 2022
Цель работы: исследование индуцированных квантовых переходов между зеемановскими уровнями неспаренного электрона в слабом магнитном поле, определение магнитного момента атома (молекулы) и времени жизни атома в возбужденном состоянии.
Рисунок 1. Установка для исследования вынужденных электронных квантовых переходов между зеемановскими уровнями атомов в слабом магнитном поле.
П
риборы: экспериментальная установка для возбуждения квантовых переходов между зеемановскими уровнями электронов – упрощенный спектрометр электронного парамагнитного резонанса (см. рис. 1)
Общие сведения
(1)
1.Электроны обладают собственным (спиновым) моментом импульса
(2)
и собственным магнитным дипольным моментом
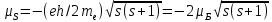
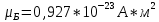
– магнетон Бора – элементарный магнитный дипольный момент. Знак минус в формуле (2) указывает на то, что направления магнитного и механического спиновых моментов вследствие отрицательности заряда электрона противоположны.
(3)
Спиновое магнитомеханическое отношение:
(5)
(4)
2. В атоме электрон может обладать также орбитальными механическим Lι и магнитным μι моментами; полные значения этих моментов характеризуются орбитальным азимутальным квантовым числом l:
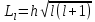
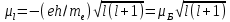
(6)
Орбитальное магнитомеханическое отношение:
3.В многоэлектронных атомах (молекулах) механические и магнитные моменты (спиновые и орбитальные) складываются так, что атом (молекула) приобретает результирующие момент импульса и магнитный дипольный момент. Правила сложения моментов обсудим только для модели так называемой рессель-саундерской связи (спин-орбитальной, LS-связи). В этой модели орбитальные моменты импульсов Ll электронов складываются в результирующий момент LL, спиновые моменты электронов Ls – в результирующий момент LS, а затем уже LL и LS обусловливают результирующий момент импульса LJ атома.
(7)
Правила сложения магнитных моментов электронов в атоме сложнее, чем механических. Числами S и L по отдельности можно характеризовать только соответственно суммарные спиновые и орбитальные магнитные моменты электронов в атоме. Соответствующий квантово-механический анализ приводит к следующему результату:
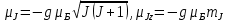
(8)
g – множитель (фактор) Ланде, определяемый по формуле
По значению фактора Ланде можно судить о вкладах орбитального и спинового движения электронов в результирующий магнитный момент атома или молекулы. Для полностью заполненных оболочек в атомах характерно равенство нулю суммарного орбитального и спинового моментов, поэтому вклад в результирующий момент атома обусловливают только электроны незаполненных оболочек.
(9)
Между зеемановскими подуровнями возможны самопроизвольные (спонтанные) и вынужденные (индуцированные) квантовые переходы с правилом отбора ΔmJ = ±1. Самопроизвольные переходы происходят только в одном направлении – с более высоких уровней на низшие. Вынужденные переходы возможны только под действием внешнего источника энергии, например внешнего электромагнитного поля. Энергия квантов поля должна совпадать с энергетическим зазором между соседними зеемановскими подуровнями:
В большом ансамбле атомов число их на нижнем (N1) и верхнем (N2) уровнях неодинаково, обычно N1 > N2. Вследствие этого число переходов с поглощением фотонов больше, нежели с излучением фотонов. Следовательно, при выполнении условия за счет индуцированных переходов между зеемановскими подуровнями из электромагнитного поля поглощается энергия. Этот эффект – электронный парамагнитный резонанс (ЭПР) – открыт в 1944 г. в СССР Е. К. Завойским.
(10)
Эффекта резонансного поглощения ансамблем атомов энергии электромагнитного поля можно достигнуть двумя способами. Подбирать частоту ν квантов электромагнитного поля для заданного поля В такой, чтобы обеспечивалось условие; частота резонансного поглощения составит тогда
(11)
Если частота ν фиксирована, можно изменением индукции поля В менять энергетический зазор между зеемановскими уровнями. Резонансное значение индукции поля В составляет
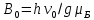
В работе применен динамический (в отличие от статического – снятия по точкам) метод наблюдения линии резонансного поглощения – многократное сканирование с частотой 50 Гц резонансного условия (16.14), как показано на рис.2, а. Для этого на резонансное поле
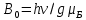c помощью дополнительных (модуляционных) катушек 3 накладывается модуляционное поле вида 
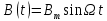, причем амплитуда модуляции Вm≥ δВ/2, где δВ –ширина резонансной линии.Из рис.2, а видно, что за период модуляции Т = 0,02 с резонансное поглощение возникает дважды между временем t1 и t2, t3 и t4, как показано на рис.2, б.
Объектом исследования в работе является дифенилпикрилгидразил (сокращенно ДФПГ) объемом 0.1 см3– мелкокристаллический порошок фиолетового цвета. Химический состав этого соединения довольно сложен; здесь лишь отметим, что каждая молекула ДФПГ имеет сильно делокализованный неспаренный электрон, для которого L ≈ 0.
Рисунок 2. Динамический метод регистрации сигналов ЭПР.
Протокол наблюдений
Лабораторная работа № 16
«Исследование электронного парамагнитного резонанса (ЭПР) в слабом магнитном поле»
Работу выполнил студент гр.1208 Титова С.А.
Таблица – 1.
| № | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
 | | | | | | | |
 | | | | | | | |
Работа выполнена « »_______________ 2022 г.
Преподаватель: Мыльников И.Л.
Обработка результатов
1. Перевод значений силы тока I в единицы индукции B.
Таблица – 1. Значение индукции B.
| № | 1 | 2 | 3 | 4 | 5 | 6 |
 | 0,25 | 0,30 | 0,35 | 0,40 | 0,45 | 0,50 |
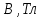 | 0,0046 | 0,0055 | 0,0064 | 0,0073 | 0,0083 | 0,0092 |
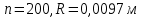
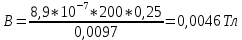
2. Расчет эффективного магнитного момента молекулы ДФПГ.
Таблица – 2. «+» направление тока в кольцах Гельмгольца.
| № | 1 | 2 | 3 | 4 | 5 | 6 |
 | 14,6 | 16,78 | 19,23 | 21,92 | 24,62 | 26,87 |
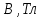| | 0,0046 | 0,0055 | 0,0064 | 0,0073 | 0,0083 | 0,0092 |
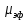 | 2,10*10-24 | 2,02*10-24 | 1,99*10-24 | 1,99*10-24 | 1,97*10-24 | 1,94*10-24 |
Таблица – 3. «-» направление тока в кольцах Гельмгольца.
| № | 1 | 2 | 3 | 4 | 5 | 6 |
| | 12,93 | 15,02 | 17,39 | 20,38 | 22,83 | 25,56 |
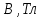| | 0,0046 | 0,0055 | 0,0064 | 0,0073 | 0,0083 | 0,0092 |
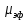| | 1,86*10-24 | 1,81*10-24 | 1,80*10-24 | 1,85*10-24 | 1,82*10-24 | 1,84*10-24 |
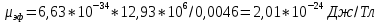
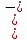
3. Расчет фактора Ланде.
Вклад дают и орбитальный, и спиновый момент движения электронов, т.к. суммарный магнитный момент не равен нулю (этот вывод можно сделать из формулы (8)), следовательно, электронные оболочки не заполнены.
Каждая молекула ДФПГ (дифенилпикрилгидразил) имеет сильно делокализованный неспаренный электрон. L≈0.
4. Расчет энергетической ширины линии резонансного поглощения. Оценка времени жизни молекулы ДФПГ в возбужденном состоянии.
Соотношение Гейзенберга-Бора:
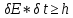
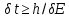
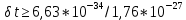
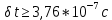(время жизни странное, порядок должен быть без минуса)5. Построение графиков зависимости частоты от индукции магнитного поля.
График -1. Зависимость ν от B.
Значение магнитного поля в лаборатории
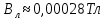
1. Что составляет основу электронного парамагнитного резонанса (ЭПР)?
Электронный парамагнитный резонанс (ЭПР) - явление резонансного поглощения электромагнитного излучения парамагнитным веществом, помещенным в постоянное магнитное поле. Обусловлен квантовыми переходами между магнитными подуровнями парамагнитных атомов и ионов (эффект Зеемана). Спектры ЭПР наблюдаются, главным образом, в диапазоне сверхвысоких частот (СВЧ).
Метод электронного парамагнитного резонанса позволяет оценить эффекты, проявляющиеся в спектрах ЭПР из-за наличия локальных магнитных полей. В свою очередь локальные магнитные поля отражают картину магнитных взаимодействий в исследуемой системе. Таким образом, метод ЭПР спектроскопии позволяет исследовать как структуру парамагнитных частиц, так и взаимодействие парамагнитных частиц с окружением.
11. В каком диапазоне лежат резонансные частоты спектра ЭПР?
ЭПР экспериментах фиксируется энергия электромагнитного кванта, то есть частота ν, а магнитное поле В может изменяться в широких пределах. Выделяются некоторые, довольно узкие, диапазоны СВЧ-частот, в которых работают спектрометры. Каждый диапазон имеет свое обозначение:
L – 1 ГГц
S – 3 ГГц
X – 9,5 ГГц
K – 24 ГГц
Q – 35 ГГц
W – 95 ГГц