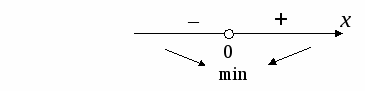Типовик № 2 «исследование Функций» По Высшой Математике (Старинец В. В.). Типовик № 2 «исследование Функций» По Высшой Математике (Старине. Исследование функций
 Скачать 181 Kb. Скачать 181 Kb.
|
|
Типовой индивидуальный расчет №2: "Исследование функций" 1. Теоретические вопросы 1. Сформулируйте теоремы Ролля, Лагранжа и Коши.
Если функция у = f(x) удовлетворяет условиям: (i) f(x) непрерывна на отрезке [а, b]; (ii) существует производная f(x) в интервале (а, b); (iii) f(a) = f(b), т. е. на концах отрезка функция принимает одинаковые значения, то существует точка с Є (а, b) такая, что f'(c) = 0. Геометрический смысл теоремы Роля: В том, что существует точка, в которой касательная горизонтальна. 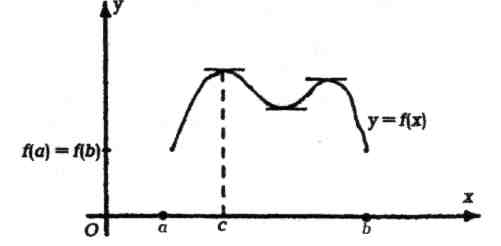 Причина этого состоит в том, что функция, принимающая на концах отрезка одинаковые значения, внутри отрезка имеет либо максимум, либо минимум. Замечание: Если хотя бы одно из условий (i) — (iii) теоремы не выполняется, то теорема Ролля может быть неверна.
Если функции у = f(x) uy=g(х) удовлетворяют условиям: (i) f(x) и q(х) непрерывны на отрезке [а, b]; (ii) существуют производные f ‘(x) и g'(х) в интервале (а,b ); (iii) g'(х) ≠ 0 в интервале (а, b), то существует точка с Є (а, b), для которой выполняется равенство
Если функция у = f{x) удовлетворяет условиям: (i) f(x) непрерывна на отрезке [а, b]; (ii) существуют производная f ’(x) в интервале (а, b), то существует точка сЄ (а, b), для которой выполняется равенство 2. Какова связь между возрастанием и убыванием функции и знаком ее производной? Если у функции у = f(x) существует производная на интервале (а, b), то функция f(x) возрастает <=> f '{x) > 0 и функция f(x) убывает <=> f ' (х) < 0 3. Какая точка называется точкой локального экстремума функции? Точка х0называется точкой локального максимума (соответственно, минимума) функции f(х), если в некоторой окрестности точки х0выполняется неравенство f{x0) ≥ f (х) (соответственноf{x0) ≤ f(x)). Точки локального максимума и минимума называются точками локального экстремума. 4. Как расположена касательная к графику функции в точке экстремума? Касательная к графику функции в точке экстремума расположена параллельно оси Ox. Т.к производная функции в этой точке равна нулю и численно совпадает с угловым коэффициентом касательной к кривой, проведенной в этой точке. 5. Сформулировать достаточные условия экстремума функции. Если функция f{x) непрерывна в окрестности точки х0, имеет производную в проколотой окрестности этой точки и если f{x) меняет знак в точке х0, то х0 — точка локального экстремума. Более точно: еслиf{x) меняет знак с' + 'на' — ', то х0 — точка локального максимума; если f(x) меняет знак с' — 'на' + ', тоx0 — точка локального минимума. 6. Дать определение выпуклости и вогнутости графика и его точек перегиба. Определение. Функция у= f{x) называется выпуклой вниз или просто выпуклой (соответственно, выпуклой вверх или вогнутой) в точке х0, если в этой точке существует касательная к графику, т.е. 3 f{x0), и в некоторой окрестности точки х0график функции лежит над (соответственно, под) касательной. Определение. Точки, в которых функция меняет направление выпуклости, т.е. меняет выпуклость на вогнутость или вогнутость на выпуклость, называются точками перегиба. 7. Какова связь между выпуклостью и вогнутостью графика и знаком ее второй производной? Пусть функция у = f(х) имеет вторую производную в окрестности точки х0, которая непрерывна в этой точке. Тогда если f"(х0) > 0, то у = f(x) выпукла, а если f'(x0) < 0, то у = f{x) вогнута в точке х0. Доказательство. Применим формулу Тейлора с остаточным членом в форме Лагранжа для функции f(х) в точке х0 при x=1: где с — некоторая точка в интервале (х0, х). Или Если теперь f "(x0) > 0, то в силу непрерывности f"(с)≥0 в некоторой окрестности точки х0, поэтому f(х) — у(х)≥0 функция выпукла. Если же f"(х0) < 0, то f'(с) < 0 поэтому f(х) — у(х) ≤0 и функция вогнута в точке х0. ■ Замечание (мнемоническое правило). Сделаем общее замечание о запоминании формул (о контроле памяти). Если вы забыли некоторое универсальное (которое действует всегда) правило, посмотрите, как оно действует в простейшем частном случае. В частности, если вы забыли, какие знаки второй производной соответствуют выпуклости и вогнутости, представьте себе мысленно графики функций у = х2 и у= =—х2. Парабола у = х2 выпукла, а у" = 2 > 0. Так же должно быть всегда. В школе для запоминания применяют «правило дождя». Замечание. Выпуклые и вогнутые функции можно охарактеризовать также следующим геометрическим свойством.  Мы видим, что если функция выпуклая (вогнутая), то при возрастании х касательные в точках х становятся более крутыми (пологими), т.е. угол наклона касательных возрастает (убывает). За угол наклона касательных отвечает f(x) = tgct. Поэтому если функция f(x) выпуклая, то f{x) возрастает и, следовательно, f'(x) > 0. И наоборот. 8. Сформулируйте достаточные условия существования точек перегиба. Если функция f(x) имеет непрерывную вторую производную f"(x) и в точке х0 f"(x) меняет знак, то х0 — точка перегиба. 9. Что называется асимптотой кривой? Что можно сказать о функции, если она имеет горизонтальную (вертикальную) асимптоту? Определение. Асимптота кривой γ—это прямая, к которой эта кривая неограниченно приближается на бесконечности, т.е. это такая прямая 1, для которой расстояние dот точки Me у до l стремится к нулю, когда точка М удаляется по кривой на бесконечность. Более точно, асимптота—это луч. Если кривая приближается к лучу, т.е. к одному «концу прямой», то говорят, что эта прямая является односторонней асимптотой. Если кривая приближается к «обоим концам» прямой, то прямая является двусторонней асимптотой. Асимптотой функции f(x) называется асимптота ее графика γ: у = f(x). 1. Если функция имеет горизонтальную асимптоту то, уравнение асимптоты имеет вид у = b = const 2. Если функция имеет вертикальную асимптоту то, что график функции “уходит на бесконечность” при x → x0 и уравнение асимптоты имеет вид x= x0 = const. 10. Необходимое и достаточное условие существования наклонной асимптоты. 2. Теоретические упражнения 1. Найти производную (если она существует) функции 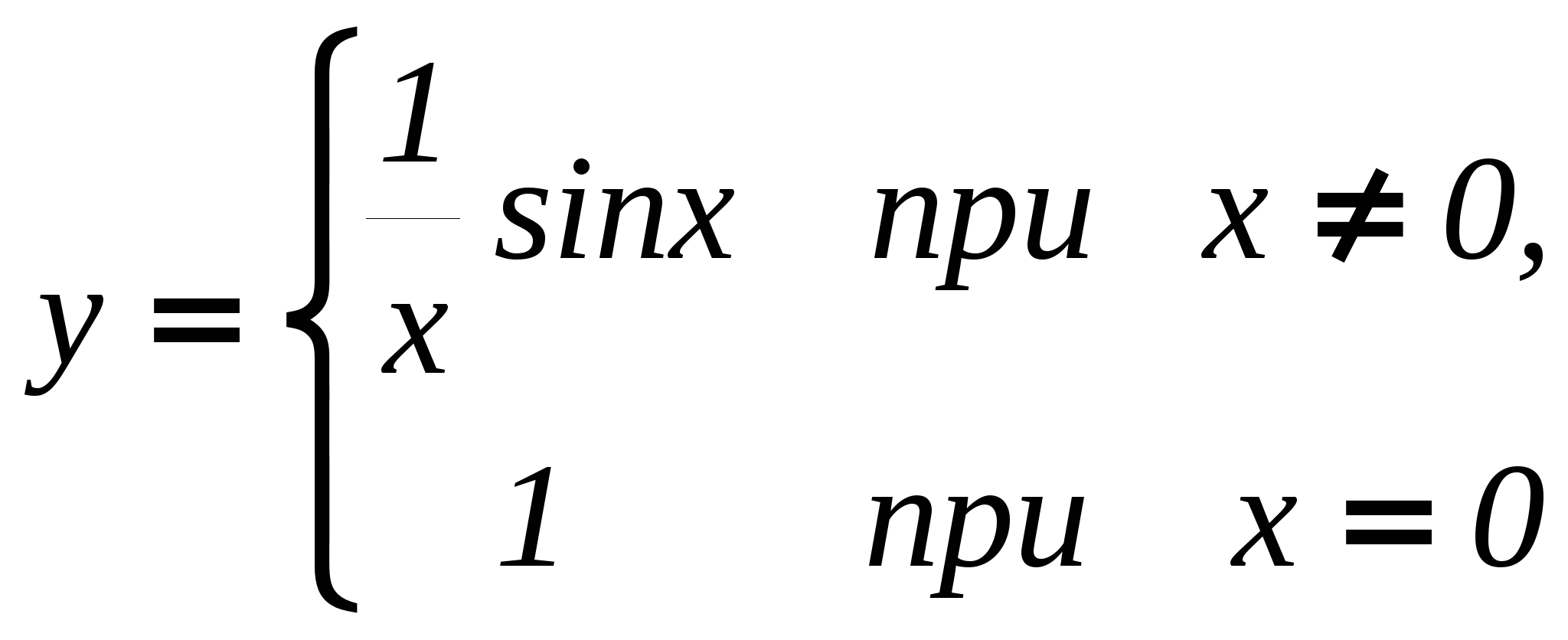 в точках х1= 0.5, х2= —0.5, х3 = 0. Решение:  2. Показать, что функция Решение: 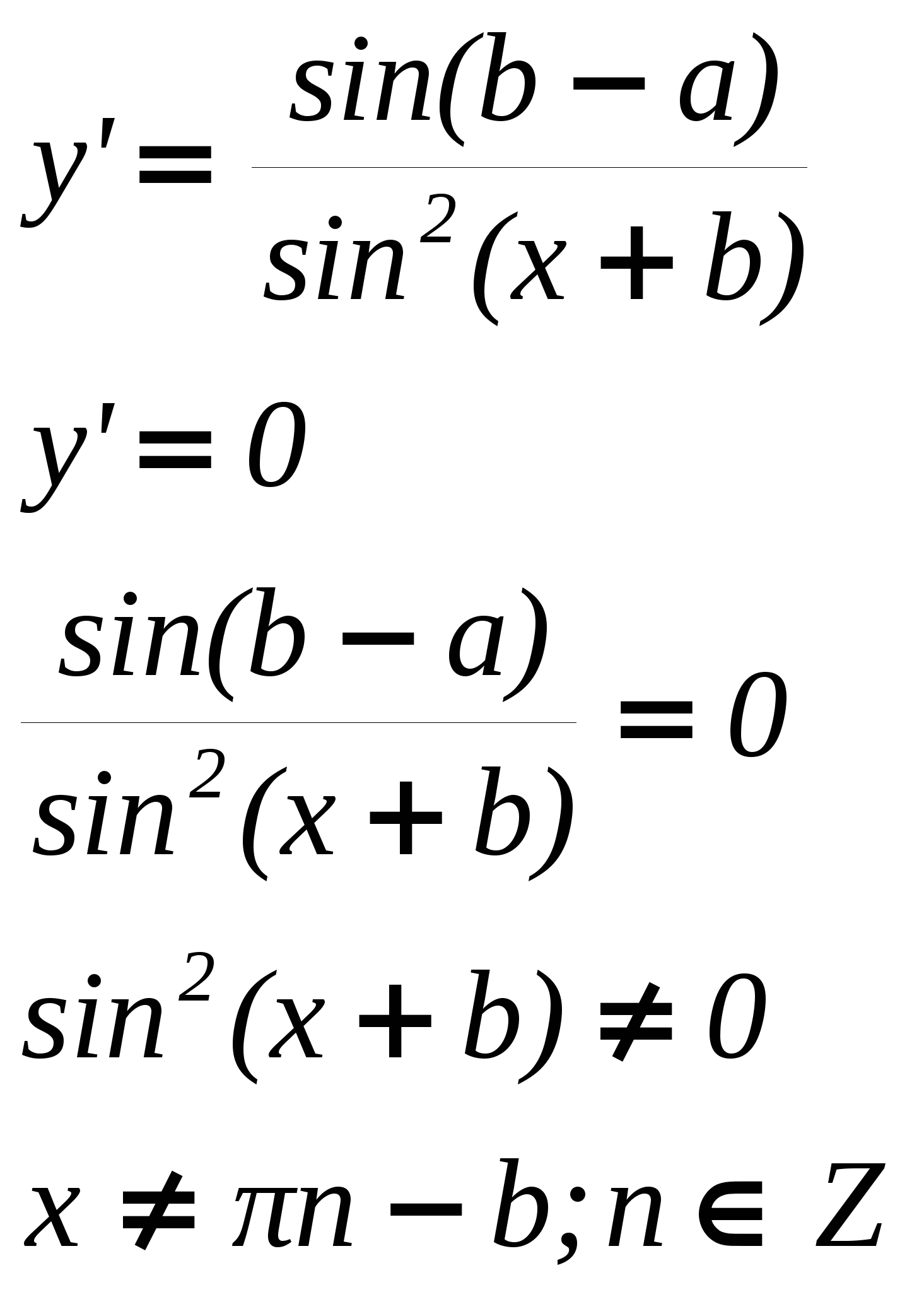 Т. К. Корни получились чётной кратности, следовательно знак производной не изменяется, следовательно функция 3. При каких значениях параметра а функция 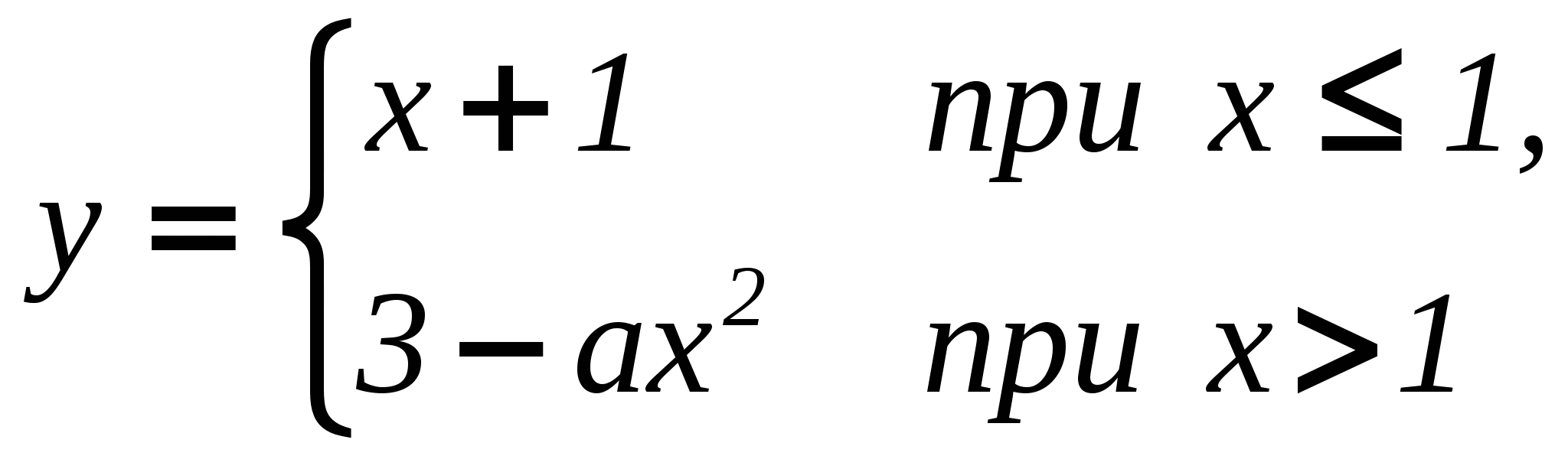 непрерывна? Постройте ее график. Решение: 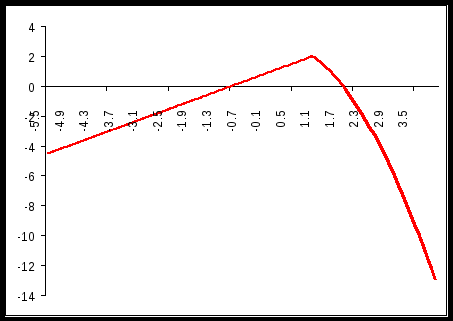  4. Выяснить вид графика функции у = f(x), если известно, что в интервале (а; b) : (1) у>0, y' >0, у"<0; (2) у>0, у' <0, у">0. Решение:   x 5. Найти асимптоты линии 6. Какое положительное число, будучи сложенным с обратным ему числом, дает наименьшую сумму? Решение: 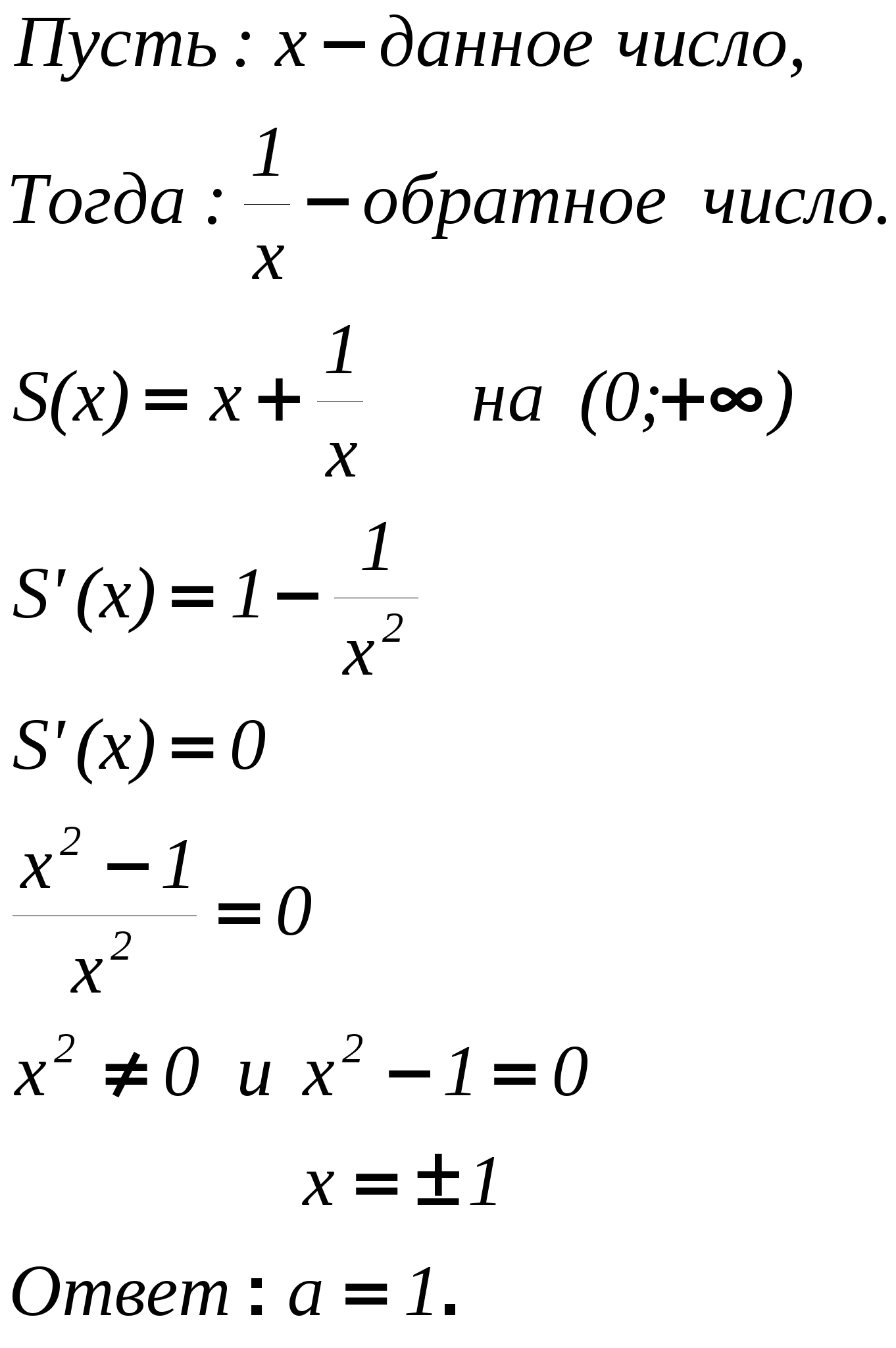 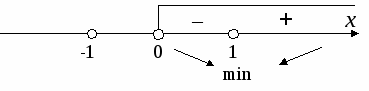 7. Доказать, что всякий четный многочлен с положительными коэффициентами является выпуклым вниз и имеет только одну точку минимума. Решение:  ─ min+ x 1   8. Доказать, что уравнение x5 + 3x—6 = 0 имеет единственный действительный корень. Решение: x5 = — 3x + 6 y1= x5 —возрастающая функция; y2= — 3x + 6 — убывающая функция. 9. Доказать, что если дифференцируемая функция четна (нечетна), то ее производная нечетна (соответственно четна). Решение: y=x2k — чётная функция. y=2kx2k-1 — нечётная функфия. y=x2k-1 — нечётная функфия. y=(2k-1)x2(k-1) — чётная функция 10. Выполняется ли на отрезке [—1, 2] теорема Ролля для функции у = х3 + 4х2 — 7х — 10? Решение: При x= —1, y=0; при x= 2, y=0; y’=3x2+8x — 7 y’=0 3x2+8x — 7=0 x1 3 Задачи Исследовать функции y=y(x) и построить их графики:
x→-
x 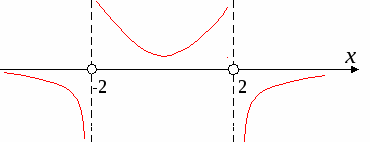 → -2+0; y→ + → -2+0; y→ +x→ -2+0; y→ - x→2+0; y→ - x→2-0; y→ +
x = —2; x = 2 —вертикальные асимптоты; y = 0 —горизонтальные асимтоты.
Уmin=3 при x=0.
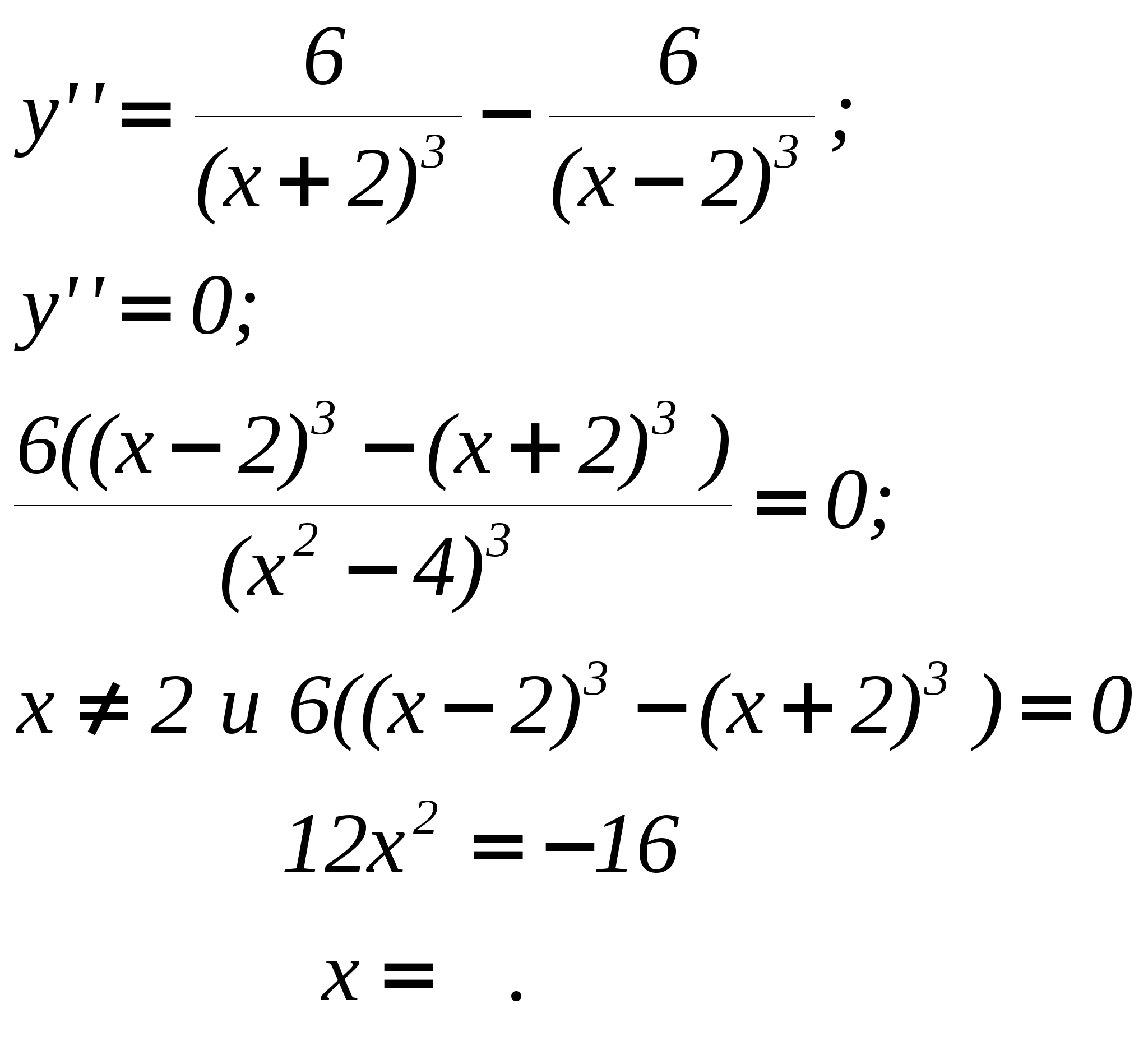   
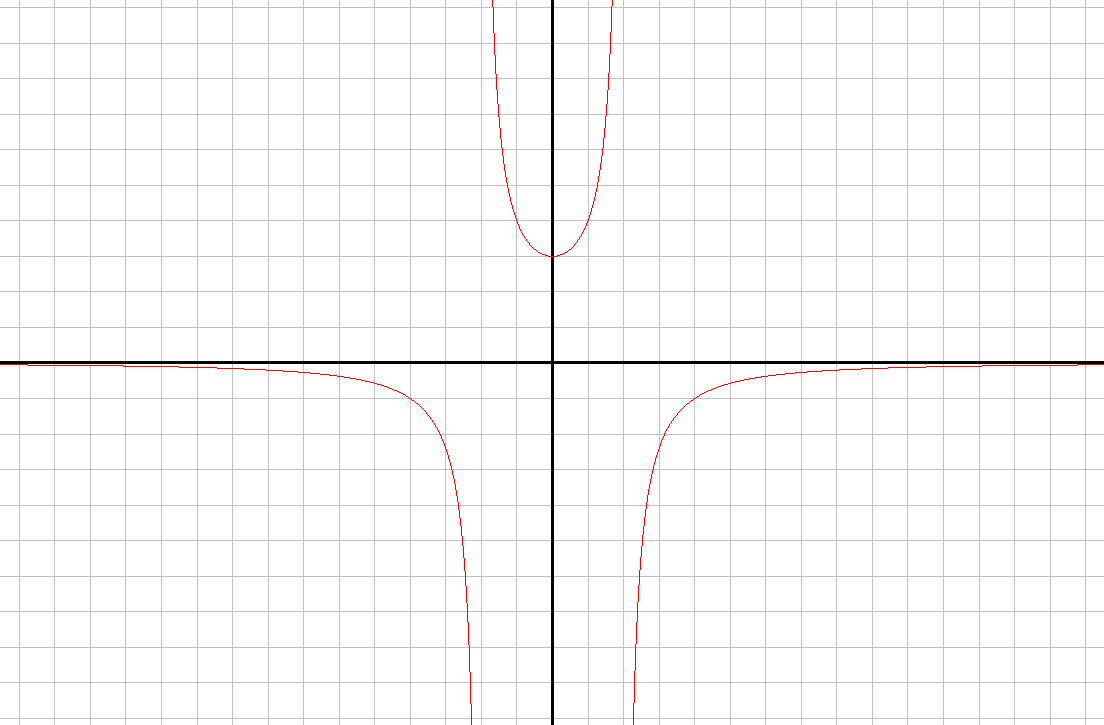
x→-
 Уmax=1 при x=2. 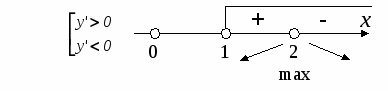
 y  2 1 -1 x -1 0 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15   |

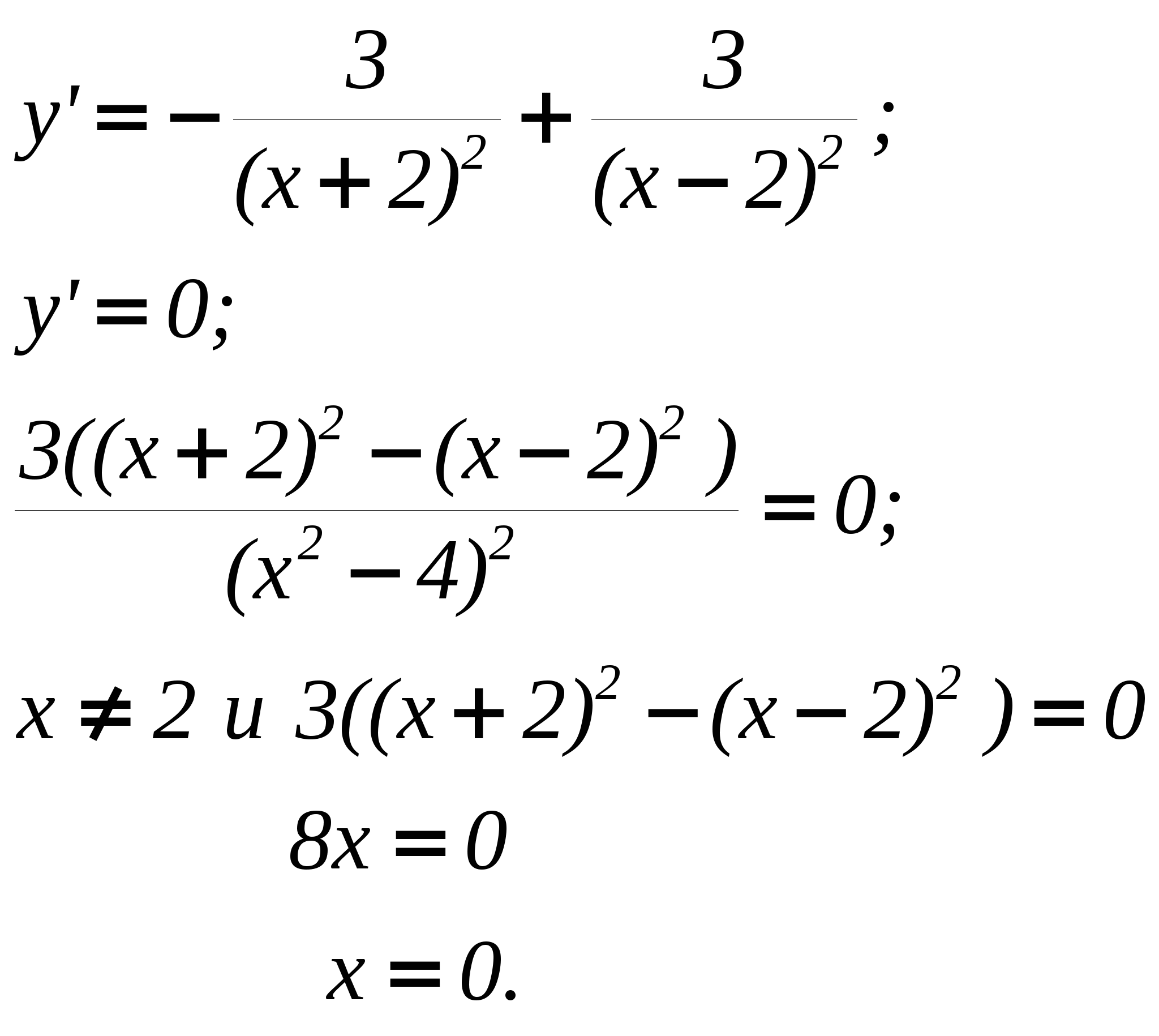 ункция дифференцируема на (-
ункция дифференцируема на (-