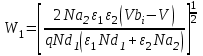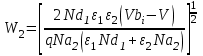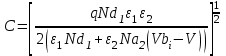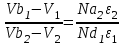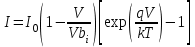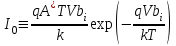|
|
Гетеропереходы и их физические свойства. Исследование гетеропереходов представляет собой важный раздел физики полупроводниковых приборов, который сформировался в последние четыре десятилетия на основе изучения эпитаксиального выращивания полупроводников
СОДЕРЖАНИЕ
ВВЕДЕНИЕ.
Исследование гетеропереходов представляет собой важный раздел физики полупроводниковых приборов, который сформировался в последние четыре десятилетия на основе изучения эпитаксиального выращивания полупроводников.
Барьеры на диаграмме энергетических зон, связанные с различием в ширине запрещенной зоны двух полупроводников открывают новые возможности для конструкторов.
Гетеропереходы используются в лазерах, вычислительной технике, интегральных схемах. Электрооптические свойства гетеропереходов нашли практическое применение в фототранзисторах и в солнечных элементах.
Однако в этой области имеется еще много нерешенных проблем, многие классы гетеропереходов еще ожидают своего тщательного изучения и применения.
Основная часть достижений в исследованиях гетеропереходов связана с использованием гетеропары GaAs-AlGaAs, в которой осуществлен так называемый идеальный гетеропереход. При этом использованы полупроводники с однотипной кристаллической решеткой, которые имеют настолько близкие значения постоянных своих решеток, что на границе не возникает электрически активных дефектов.
Однако физика и техника гетеропереходов имеют и другой важный аспект - создание, исследование и практическое применение неидеальных гетеропереходов. Такие структуры образованы поликристаллическими полупроводниками с несовпадающими константами кристаллических решеток, зачастую и различных решеточных симметрии. В неидеальных гетеропереходах наблюдается большой набор различных эффектов и явлений, связанных с различными свойствами полупроводников по обе стороны границы, а также с появлением большого количества электрически активных дефектов на гетерогранице, принимающих участие в токопереносе, поглощении и излучении световых квантов.
Перспективность практического применения неидеальных гетеропереходов связана в первую очередь с более экономичной технологией создания поликристаллических гетероструктур в сравнении с монокристаллическими.
Одним из направлений в изучении неидеальных гетеропереходов является возможность применения критериев, разработанных в классической фотографической сенситометрии, к преобразователям оптического изображения в электрический сигнал на основе гетероперехода CdS-Cu2S.
Целью данной работы является создание математической модели характеристической кривой и расчет основных сенситометрических характеристик (γ-коэфициент контрастности и S-фоточувствительность) формирователя сигнала изображения (ФСИ) на основе гетероперехода CdS-Cu2S, используя в качестве исходных данных характеристики локальных центров в гетеропереходе.
ГЛАВА I. ГЕТЕРОПЕРЕХОД CdS-Cu2S, ЕГО СВОЙСТВА И ТЕХНОЛОГИЯ ИЗГОТОВЛЕНИЯ.
§ 1. Общие свойства гетеропереходов.
Гетеропереходом называется контакт двух различных по химическому составу полупроводников. Если полупроводники имеют одинаковый тип проводимости, то они образуют изотипный гетеропереход. Если тип их проводимости различен, то получается анизотипный гетеропереход.
Для получения идеальных монокристаллических гетеропереходов без дефектов решетки и поверхностных состояний на границе раздела необходимо, чтобы у полупроводников совпадали типы кристаллических решеток, их периоды и коэффициент термического расширения. Для их получения периоды решеток должны совпадать с точностью 0,1%. Пример идеального гетероперехода: GaAS -AIGaAS [1].
Модель зоны структуры идеального резкого гетероперехода без ловушек на границе раздела была предложена Андерсеном, который использовал результаты работы Шокли [2].
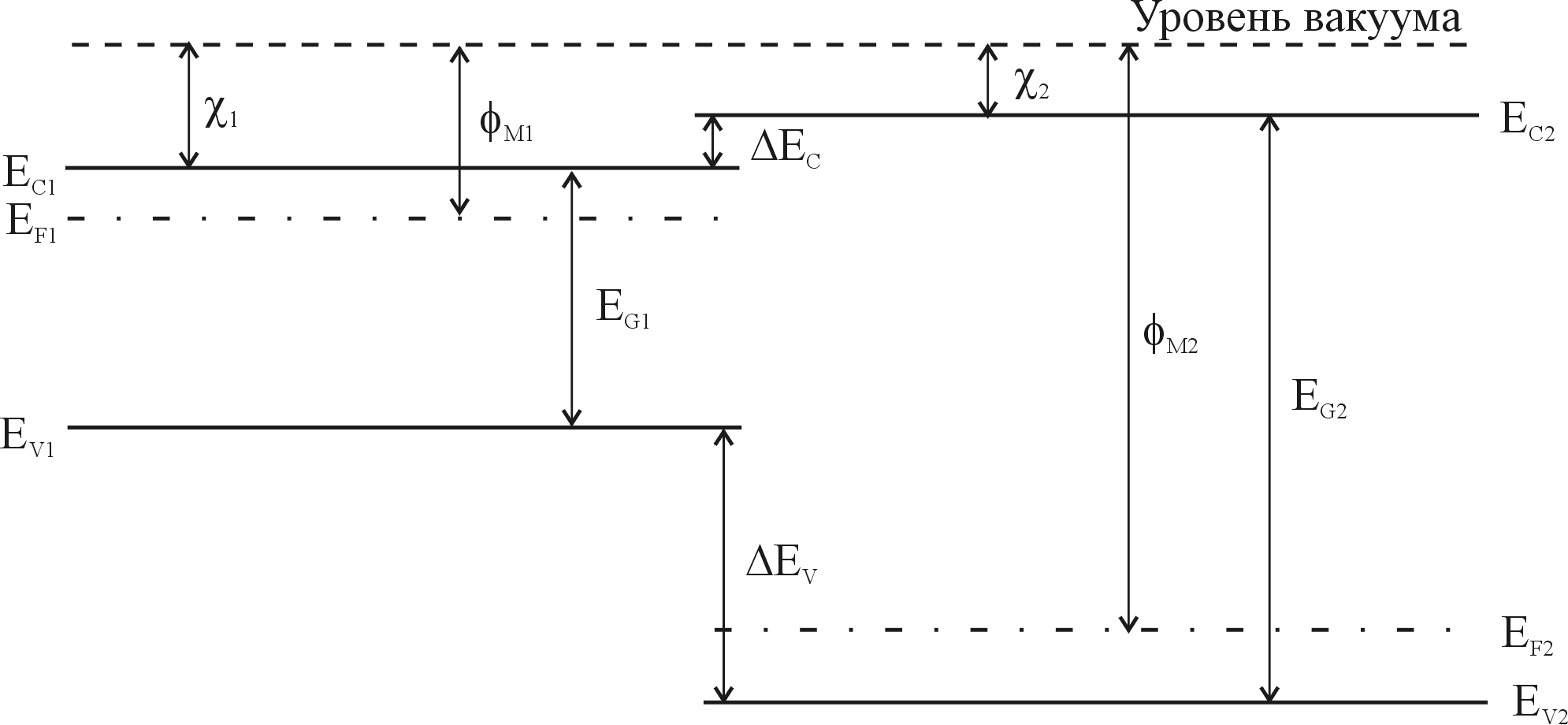
На рис.1 приведена зонная диаграмма двух изолированных полупроводников, у которых различные значения ширины запрещенной зоны Еg , диэлектрической проницаемости , работы выхода m и электронного сродства .
Работа выхода и электронное сродство определяются как энергия, необходимая для удаления электрона с уровня Ферми Еf и со дна зоны проводимости Еc в вакуум соответственно. Различие в положении дна зоны проводимости полупроводников обозначено Еc; а различие в положении потолка валентной зоны ΔEv. На рисунке 1 показан случай, когда ΔЕc=(χ1-χ2).
|
|
Рис. 1. Зонная диаграмма двух изолированных полупроводников при условии электронейтральности
|
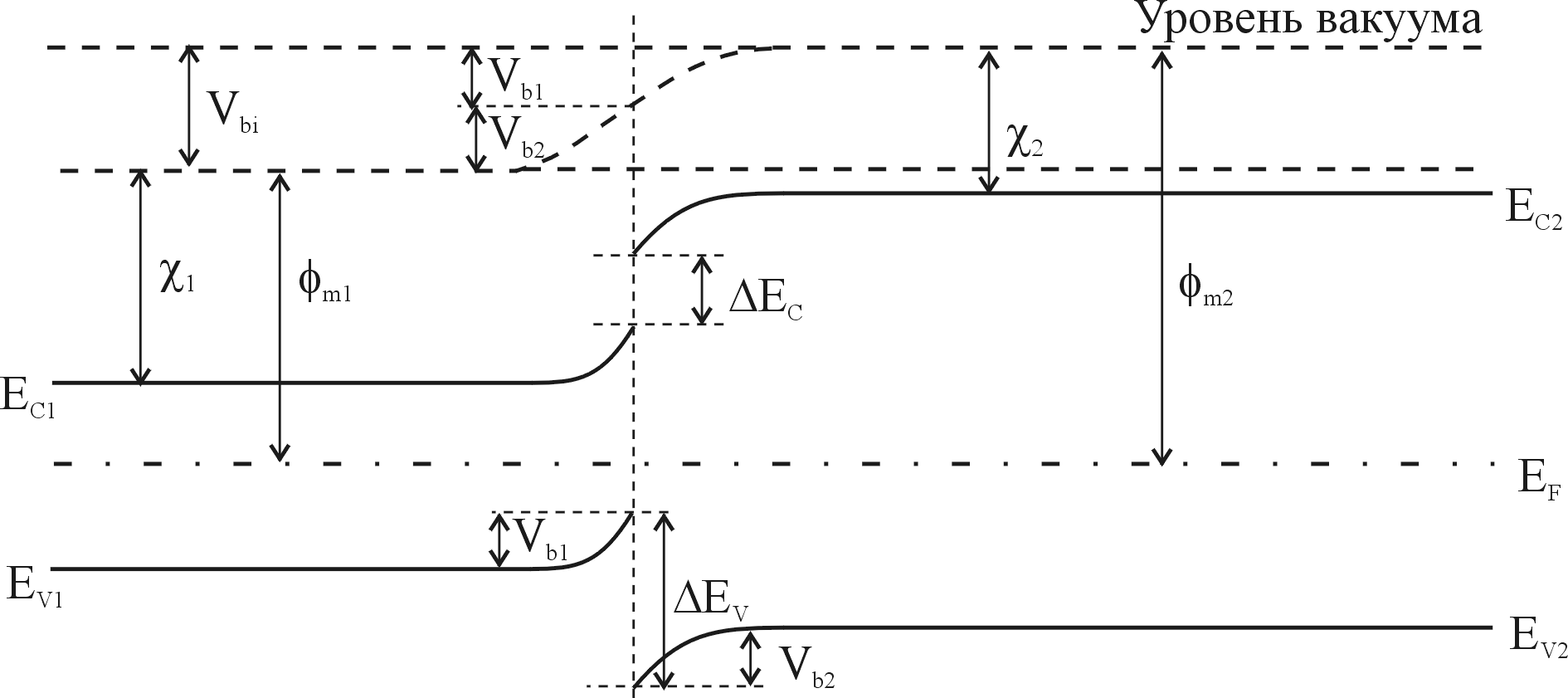
Зонная диаграмма анизотипного p-n - гетероперехода в равновесии, образованного этими полупроводниками приведена на рис.2.
|
|
Рис.2. Зонная диаграмма идеального анизотипного p-n гетероперехода при тепловом равновесии.
|
Положение уровня Ферми в равновесном состоянии должно быть одинаково по обе стороны перехода, а уровень энергии, соответствующий вакууму, должен быть параллелен краям зон и непрерывен. Поэтому разрыв в положении краев зоны проводимости и краев валентной зоны не связан с уровнем легирования.
Полный контактный потенциал Vbi. равен сумме потенциалов Vb1+Vb2, где Vb1 и Vb2 - электростатические потенциалы равновесия состояния первого и второго полупроводников соответственно.
Ширину обедненного слоя (W) в каждом полупроводнике и барьерную емкость (С) можно найти решив уравнение Пуассона для резкого перехода с каждой стороны границы раздела. Одним из граничных условий является непрерывность электрической индукции на границе раздела, т.е. ε1E1= ε2E2. В результате имеем:
где Nd1 - концентрация доноров в 1-м полупроводнике;
Na2 - концентрация акцепторов во 2-м полупроводнике.
Отношение напряжений в каждом полупроводнике составляет:
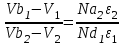
|
(4)
|
где V=V1+V2 - полное приложенное напряжение.
Вольт - амперная характеристика принимает вид:
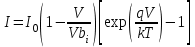
|
(5)
|
где I - плотность тока.
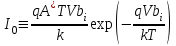
|
(6)
| |
|
|
 Скачать 314.46 Kb.
Скачать 314.46 Kb.