ПЕРЕДАТОЧНЫЕ ФУНКЦИИ И УРАВНЕНИЯ СОСТОЯНИЯ. ПР1_ТАУ. Исследование и применение методов получения уравнений состояния из объекта управления, описанного передаточной функцией
 Скачать 112.3 Kb. Скачать 112.3 Kb.
|
|
Цель работы Исследование и применение методов получения уравнений состояния из объекта управления, описанного передаточной функцией. Исходные данные Для заданной передаточной функции получить двумя способами описание в пространстве состояний (матрицы A, B, C, D). Проверить полученное описание моделированием в MatLab. Вариант 5 – 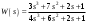 . .Расчетная часть Изначально будет получено для заданной передаточной функции описание в пространстве состояний первым способом. Имеется ПФ управления: 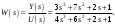 Необходимо домножить на 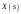 числитель и знаменатель ПФ. числитель и знаменатель ПФ.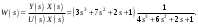 Из данного выражения можно записать уравнение состояния: 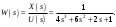 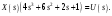 Переходя во временную область, можно получить данное выражение: 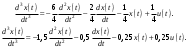 В нем необходимо выбрать переменные состояния: 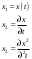  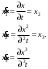 Тогда можно записать: 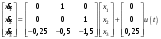 . .Теперь необходимо записать уравнение выхода: 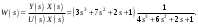 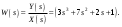 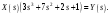 Переходя во временную область, можно получить выражение: 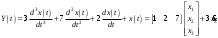 . .Используя полученное описание для 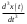 , следует: , следует: 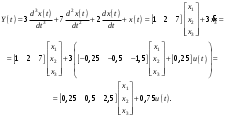 Ниже будет выполнена проверка решения в системе MatLab, рассмотрев реакцию на единичный скачок исходной системы, заданной передаточной функцией и системы, описанной в пространстве состояний. >>W=tf([3 7 2 1],[4 6 2 1]); >>A=[0 1 0; 0 0 1; -0.25 -0.5 -1.5]; >>B=[0; 0; 0.25]; >>C=[0.25 0.5 2.5]; >>D=0.75; >>W1=ss(A,B,C,D); >>[Y1,T]=step(W); >>[Y2,T]=step(W1); >>plot(T,Y1,T,Y2); >>grid; >>xlabel('t, c'); >>ylabel('Y1(t), Y2(t)') На рисунке 1 представлены графики переходных процессов, они оказались идентичны. 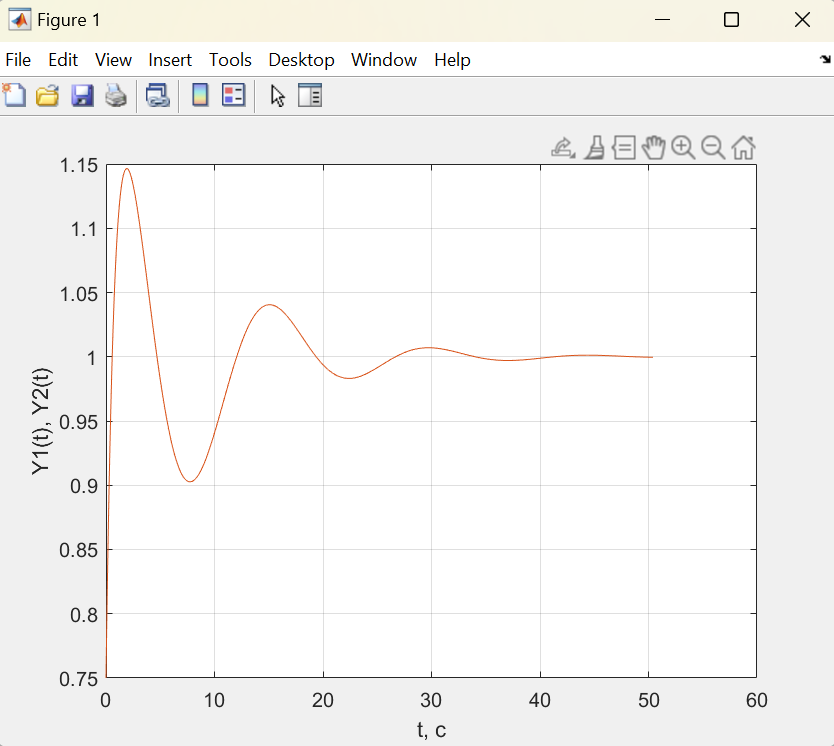 Рисунок 1 – Графики переходных процессов Теперь будет получено для заданной передаточной функции описание в пространстве состояний вторым способом. Имеется ПФ управления: 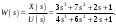 Здесь имеется: 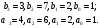 Уравнения состояния в канонической форме управляемости приобретают вид: 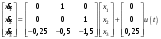 . .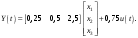 Ниже будет выполнена проверка решения в системе MatLab, рассмотрев реакцию на единичный скачок исходной системы, заданной передаточной функцией и системы, описанной в пространстве состояний. >>W=tf([3 7 2 1],[4 6 2 1]); >>A=[0 1 0; 0 0 1; -0.25 -0.5 -1.5]; >>B=[0; 0; 0.25]; >>C=[0.25 0.5 2.5]; >>D=0.75; >>W1=ss(A,B,C,D); >>[Y1,T]=step(W); >>[Y2,T]=step(W1); >>plot(T,Y1,T,Y2); >>grid; >>xlabel('t, c'); >>ylabel('Y1(t), Y2(t)') На рисунке 2 представлены графики переходных процессов, они оказались идентичны.  Рисунок 2 – Графики переходных процессов Вывод В ходе данной практической работы были получены навыки в исследовании и применении методов получения уравнений состояния из объекта управления, описанного передаточной функцией. |
