Контрольные вопросы ЦОИ. Контрольные вопросы. Контрольные вопросы Дайте определение их
 Скачать 133 Kb. Скачать 133 Kb.
|
|
Контрольные вопросы: 1. Дайте определение ИХ. Импульсной характеристикой h(n) ЛДС называют ее реакцию на цифровой единичный импульс u0n={1, n=0 0, n≠0 при ННУ. 2.Запишите формулу свертки. Соотношение вход/выход ЛДС, однозначно связанное с его основной характеристикой во временной области — ИХ, имеет вид линейного математического преобразования в виде формулы свертки: 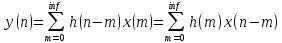 3.Поясните, как в формуле свертки учитываются ННУ. В отличие от линейных аналоговых систем, где соответствующие соотношения вход, выход имеют вид интеграла свертки или линейного дифференциального уравнения, вычисление реакции по формуле свертки или РУ выполняется методом прямой подстановки при ННУ, т. е. эти соотношения непосредственно описывают алгоритмы вычисления реакции. 4. Запишите РУ общего вида. Соотношение вход/выход ЛДС, однозначно связанное с его основной характеристикой в z-области — передаточной функцией (о которой пойдет речь в разд. 8.1.2), имеет вид линейного математического преобразования в виде разностного уравнения (РУ): 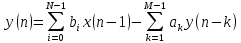 5. Поясните, как в РУ учитываются ННУ. В отличие от линейных аналоговых систем, где соответствующие соотношения вход, выход имеют вид интеграла свертки или линейного дифференциального уравнения, вычисление реакции по формуле свертки или РУ выполняется методом прямой подстановки при ННУ, т. е. эти соотношения непосредственно описывают алгоритмы вычисления реакции. 6. Дайте определение рекурсивных и нерекурсивных ЛДС. Рекурсивная ЛДС, реакция которой зависит от текущего и предшествующих отсчетов воздействия и предшествующих отсчетов реакции, т. е.: ak≠0 хотя бы для одного значения k Нерекурсивная ЛДС, реакция которой зависит только от текущего и предшествующих отсчетов воздействия, т. е.: ak=0 для всех k 7.Поясните принципиальное отличие ИХ рекурсивных и нерекурсивных ЛДС. Рекурсивные и нерекурсивные ЛДС имеют соответственно бесконечную и конечную ИХ, отсюда их тождественные названия: БИХ ЛДС (IIR – Infinite Impulse Response); КИХ ЛДС (FIR – Finite Impulse Response). 8.Приведите тождественные названия рекурсивных и нерекурсивных ЛДС. БИХ ЛДС (IIR – Infinite Impulse Response); КИХ ЛДС (FIR – Finite Impulse Response). Импульсная характеристика КИХ ЛДС совпадает с коэффициентами bi РУ Hn=bi, n=i 9.Дайте определение передаточной функции. Основной характеристикой ЛДС в z-области является передаточная функция H(z) — z-изображение ИХ h(n): 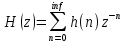 Передаточной функцией ЛДС называют отношение z-изображения реакции к z-изображению воздействия при ННУ: Hz=Y(z)/X(z) 10.Запишите общий вид передаточной функции рекурсивной ЛДС. Общий вид ПФ представлен дробно-рациональной функцией: 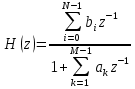 11.Приведите основные разновидности передаточной функции рекурсивной ЛДС. 1. Произведение простейших множителей: H(z)= 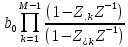 Где z∙k, z*k — соответственно k-е нуль и полюс передаточной функции. В общем случае нули и полюсы — попарно комплексно сопряженные числа; 2. Произведение множителей второго порядка: н9 Где 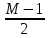 ), где int — функция округления до ближайшего целого в сторону увеличения. ), где int — функция округления до ближайшего целого в сторону увеличения.3. Сумма простых дробей: 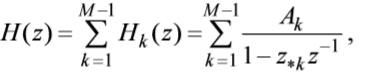 Где z*k —простой (не кратный) k-й полюс передаточной функции; Ak— коэффициент разложения при k-м полюсе; Ak и z*k— всегда числа одинакового типа, комплексные или вещественные. При M-1=(N-1) будем иметь целую часть — вещественную константу C: 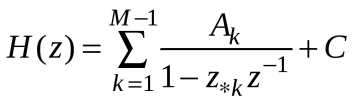 12.Запишите передаточную функцию нерекурсивной ЛДС. Для нерекурсивных ЛДС ПФ принимает вид рациональной функции 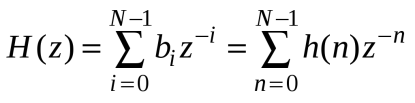 13.Что такое нули и полюсы ЛДС? Нулями передаточной функции называют значения z, при которых она равна нулю, а полюсами (особыми точками) — значения z, при которых ее знаменатель равен нулю. 14.Что такое карта нулей и полюсов? Картой нулей и полюсов называют z-плоскость с нанесенной единичной окружностью и символически изображенными нулями и полюсами Карта нулей и полюсов передаточной функции выводится с помощью функции: zplane(b,a) Известно, что любая схемная функция является дробно-рациональной функцией комплексной переменной "p": 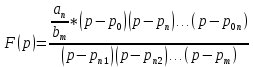 Если корни полинома числителя и знаменателя отобразить на комплексной плоскости, то мы получим ,так называемую, карту нулей и полюсов. На карте нули изображаются кружочками, а полюса крестиками. 15.Дайте определение устойчивости ЛДС. ЛДС называется устойчивой, если при ограниченном воздействии mах|х(ги)| < Rx, где Rx - любое сколь угодно большое положительное число, не равное бесконечности, и произвольных, но ограниченных начальных условиях реакция будет также ограниченной max|y(/n)| 16. Как определить, является ли ЛДС устойчивой? По карте нулей и полюсов можно сделать вывод об устойчивости ЛДС: полюсы устойчивой ЛДС располагаются внутри единичного круга 17.Дайте определения АЧХ и ФЧХ. Амплитудно-частотной характеристикой ЛДС A() называется частотная зависимость отношения амплитуды реакции к амплитуде дискретного гармонического воздействия в установившемся режиме. Фазочастотной характеристикой ЛДС () называется называется частотная зависимость разности фазы реакции и фазы дискретного гармонического воздействия в установившемся режиме. 18. Поясните связь частотной характеристики с передаточной функцией. Частотная характеристика (ЧХ) H( 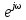 ) связана с передаточной функцией соотношением H( ) связана с передаточной функцией соотношением H(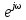 )= )= 19.Перечислите основные свойства АЧХ и ФЧХ. АЧХ и ФЧХ дискретного сигнала — непрерывные функции частоты. АЧХ и ФЧХ дискретного сигнала — периодические функции частоты с периодом Таким образом, в частотной области следствием перехода АЧХ — четная, а ФЧХ — нечетная функция частоты. 20.Приведите определение и поясните смысл нормированной частоты . Нормированная частота – абсолютная частота, нормированная к частоте дискретизации: f=  21.В какой полосе частот и почему рассчитывают АЧХ и ФЧХ? АЧХ и ФЧХ рассчитываются в основной полосе частот. В шкале основная полоса равна ∈(0;  ) )В шкале f основная полоса равна f∈(0;fд/2) В шкале частот основная полоса равна ∈(0; д/2)  прямая транспонированная — Direct-Form I Transposed;  прямая каноническая — Direct-Form II;  прямая каноническая транспонированная — Direct-Form II Transposed; |
