Математическое моделирование. мат моделирование 2 задача. Исследование напряженного состояния в точке упругого тела с помощью базы знаний WolframAlpha в курсе Сопротивление материалов

• Название: Исследование напряженного состояния в точке упругого тела с помощью базы знаний WolframAlpha в курсе Сопротивление материалов
• Анкор: Математическое моделирование
• Дата: 22.06.2021
• Размер: 0.58 Mb.
• Имя файла: мат моделирование 2 задача.docx
• Тип: Исследование; #220402

Попов С. Д., Сорокин А. Н., Клоков А. С. Исследование напряженного состояния в точке упругого тела с помощью базы знаний WolframAlpha в курсе «Сопротивление материалов» // Электронный научнометодический журнал Омского ГАУ. - 2017. -№2 (9) апрель – июнь. - URL http://ejournal.omgau.ru/images/issues/2017/2/00353.pdf. - ISSN 2413-4066

УДК 378.14

Попов Сергей Дмитриевич Старший преподаватель ФГБОУ ВО Омский ГАУ, г. Омск.

[e-mail]

Сорокин Анатолий Никифорович Кандидат технических наук, доцент ФГБОУ ВО Омский ГАУ, г. Омск.

[e-mail]

Клоков Александр Сергеевич

Кандидат физико-математических наук, доцент

ФГБОУ ВО Омский ГАУ, г. Омск

[e-mail]

Исследование напряженного состояния в точке упругого тела с помощью базы знаний WolframAlpha в курсе «Сопротивление материалов»

Аннотация: В статье рассмотрена задача исследования напряженного состояния в точке упругого тела. Показана эффективность применения базы знаний WolframAlpha для решения этой задачи. Данная методика может быть рекомендована для преподавателей и обучающихся при изучении курса «Сопротивление материалов».

Ключевые слова: база знаний WolframAlpha, сопротивление материалов, напряженное состояние, главные напряжения, направляющие косинусы, тензор напряжений.

Учебные задачи по курсу «Сопротивление материалов», как правило, содержат большой объем численных расчетов. В некоторых случаях их выполнение невозможно без применения специальных программ. Например, в работе [1] рассмотрено использование системы Mathcad, позволяющей получать простые решения сложных задач. Однако, данная система является лицензионной ввиду чего доступ к ней обучающихся затруднен. Вместе с тем, существует набор вычислительных алгоритмов в базе знаний WolframAlpha, находящейся в свободном доступе по адресу http://www.wolframalpha.com/ [2], используемый, например, в теоретической механике [3], который также можно успешно использовать для решения многих задач по сопротивлению материалов. Какой-то специальной подготовки для использования этой базы знаний не требуется.

Проиллюстрируем использование базы знаний WolframAlpha для анализа напряженного состояния в точке упругого тела.

Под действием приложенных внешних сил в теле появляются внутренние силы, для определения которых используется метод сечений. Тело мысленно рассекается плоскостью на две части, одна из них отбрасывается, а её действие на оставшуюся часть заменяется силами, распределенными по сечению. Интенсивность этих сил (x, y, z) называется полным напряжением в точке тела. Проекция на нормаль к сечению называется нормальным напряжением и обозначается , проекция на плоскость сечения называется касательным напряжением и обозначается . Модуль полного напряжения

.

Полное напряжение не считается удобной мерой оценки интенсивности внутренних сил, так как материалы различным образом сопротивляются действию нормальных и касательных напряжений.

Напряженным состоянием в точке называется совокупность напряжений, которые действуют на различных площадках, проведенных через точку тела находящегося под действием внешних сил. Если в окрестности произвольной точки мысленно вырезать элементарный параллелепипед с размерами dx, dy, dz, то вектор полного напряжения на каждой его грани можно разложить по координатным осям на три составляющие – нормальное напряжение и два касательных напряжения (рис. 1).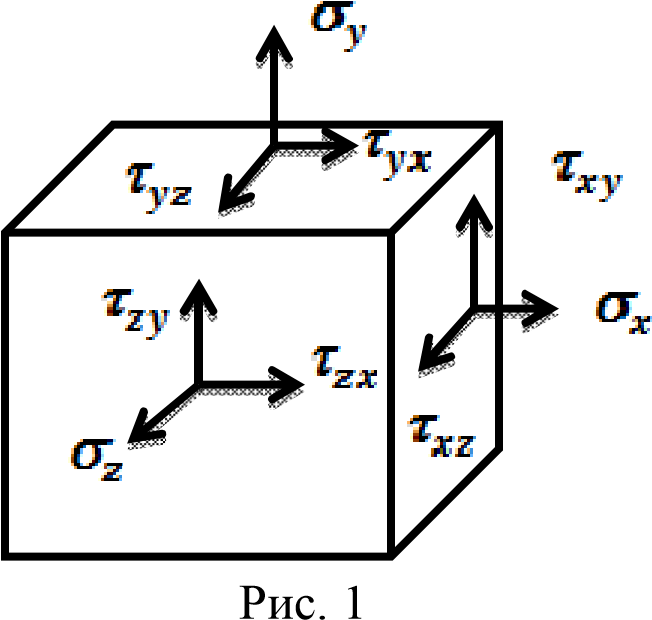



На противоположных гранях элемента действуют такие же по величине, но противоположно направленные напряжения. Первый индекс в обозначении напряжений указывает направление нормали к площадке, а второй индекс – направление оси проекции. По закону парности касательные напряжения на взаимно перпендикулярных площадках равны:

; .

Поэтому напряженное состояние в точке тела определяется шестью независимыми напряжениями.

Если вращать элемент вокруг осей координат, то можно найти такое его положение, при котором касательные напряжения на его гранях будут равны нулю. Площадки, на которых касательные напряжения равны нулю, называются главными, а нормальные напряжения на главных площадках называются главными напряжениями и обозначаются σ₁, σ₂, σ₃.

Различают три вида напряженного состояния:

• 
  линейное – когда одно из главных напряжений не равно нулю; - плоское – когда два главных напряжения не равны нулю;
  
• 
  объемное – когда три главных напряжения не равны нулю.
  

Между главными напряжениями существует соотношение:

.

В основе расчетов на прочность лежит условие прочности:

или .

То есть наибольшие напряжения, нормальные или касательные, в опасной точке не должны превышать допускаемых напряжений [σ] или [τ].

Если напряженное состояние линейное, то предельное состояние легко установить экспериментально. Опасным состоянием для пластичных материалов является предел текучести σ_т, а для хрупких – предел прочности σ_в

,

где [σ₊] и [σ_–] – допускаемые напряжения при растяжении и сжатии соответственно.

При сложном напряженном состоянии это сделать практически невозможно и для выбора критерия прочности вводятся гипотезы о преимущественном влиянии на прочность различных факторов. Эти гипотезы называют теориями прочности. С их помощью плоское или объемное напряженное состояние сводится к эквивалентному ему по действию линейному. Например, по четвертой теории прочности предполагается, что предельное состояние нагруженного тела определяется предельной величиной накопленной удельной энергии формоизменения, откуда следует [4]:

.

Эта теория применима для пластичных материалов, одинаково сопротивляющихся растяжению и сжатию.

Следовательно, определение вида напряженного состояния и главных напряжений является неотъемлемой частью расчетов на прочность.

В большинстве учебников по сопротивлению материалов рассмотрены методы определения положения главных площадок и главных напряжений при плоском и линейном напряженном состояниях. Например, согласно [5] главные напряжения при плоском напряженном состоянии определяются по формуле: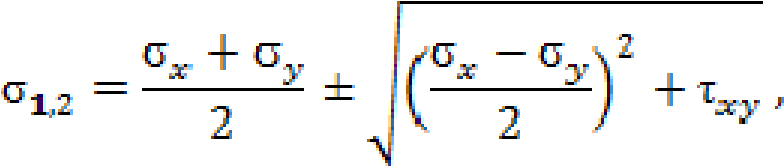



а положение главных площадок по формулам:



где ₁ и ₂ – углы, определяющие положение главных площадок (рис. 2).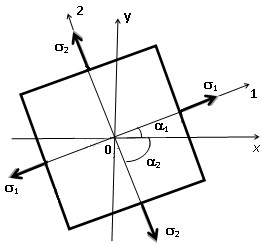



Рис. 2

Для иллюстрации объемного напряженного состояния, как правило используется графический способ – круг напряжений (круг Мора). Между тем существует методика исследования объемного напряженного состояния аналитическими методами, которая подробно описана, например, в [6].

Запишем напряжения, действующие по граням элемента в виде квадратной матрицы. Каждый столбец такой матрицы представляет собой совокупность напряжений на одной из граней элемента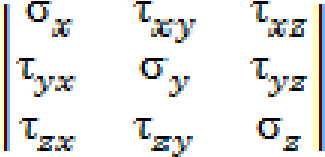

.

Можно показать, что эта матрица является тензором, компоненты которого подчиняются правилам преобразования тензорной алгебры. Для определения величины главных напряжений используется кубическое уравнение

, (1)

где выражения для определения коэффициентов получены при развертывании определителя:

;

;

(2)

.

Здесь I₁, I₂, I₃ являются инвариантами преобразования составляющих тензора напряжений при повороте осей координат. Так как все характеристические числа вещественной симметричной матрицы вещественны, то кубическое уравнение имеет три вещественных корня, которые следует пронумеровать в порядке убывания:

.

Это и будут главные напряжения.

Для определения направляющих косинусов l_i, m_i, n_i нормалей главных площадок (i = 1, 2, 3) используется система уравнений: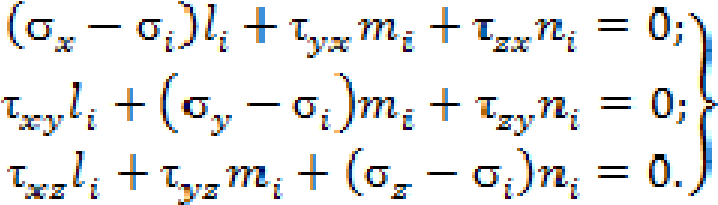

(3)

При дополнительном условии

(4)

нормали к главным площадкам образуют систему трех взаимно перпендикулярных осей, называемых главными осями напряженного состояния в точке упругого тела.

Рассмотрим применение базы знаний WolframAlpha на примере из учебника [1]. Напряженное состояние задано в виде тензора напряжений Т_σ

.

Для определения главных напряжений и косинусов углов между нормалями к главным площадкам и исходными осями координат x, y, z (направляющих косинусов) в рассматриваемом примере используются функции eigenvals и eigenvecs системы Mathcad. В результате решения получаются следующие главные напряжения: σ₁ = 111,178 МПа; σ₂ = 53,28 МПа; σ₃ = – 114,458 МПа. Направляющие косинусы равны: l = 0,241; m = – 0,959; n = – 0,147.

Для того, чтобы решить эту задачу с помощью WolframAlpha введем следующие обозначения: σ_x = a, σ_y = b, σ_z = c, τ_xy = d, τ_xz = h, τ_yz = f. Тогда уравнение (1) с учетом (2) примет следующий вид:



.

Эта форма записи кубического уравнения (1) удобна для формирования запросов, вводимых в командную строку базы знаний WolframAlpha, позволяющих находить решения данного уравнения для конкретных числовых значений a, b, c, d, f, h. В рассматриваемой задаче этот запрос имеет вид:

solve [ sigma^3-(50+100-100)*sigma^2+(50*100+100*(-100)+50*(-100)-(-20)^2-40^230^2)*sigma-(50*100*(-100)-50*40^2-100*30^2-(-100)*(-20)^2+2*(-20)*40*30)=0]

Решение уравнения представлено на рис. 3.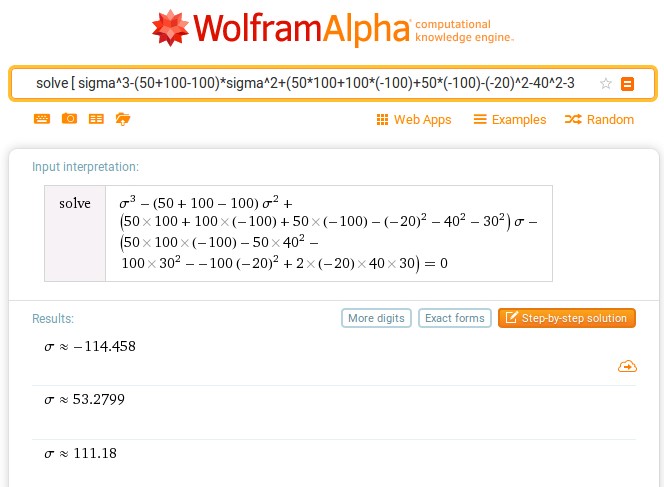



Рис. 3

Таким образом, главные напряжения σ₁ = 111,18 МПа; σ₂ = 53,2799 МПа; σ₃ = – 114,458 МПа совпадают с решением, полученным в системе Mathcad [1].

Для определения направляющих косинусов l_i, m_i, n_i, используя уравнения (3), (4), составляем три системы уравнений. Запросы для их решения с помощью базы знаний WolframAlpha для заданного тензора напряжений имеют вид:

solve [(50-111.18)*l-20*m+30*n=0, -20*l+(100-111.18)*m+40*n=0, l^2+m^2+n^2=1]]

solve [(50-53.2799)*l-20*m+30*n=0, -20*l+(100-53.2799)*m+40*n=0, l^2+m^2+n^2=1]

solve [(50+114.458)*l-20*m+30*n=0, -20*l+(100+114.458)*m+40*n=0, l^2+m^2+n^2=1]

а их решения представлены на рис. 4, 5, 6 соответственно.



Рис. 4



Рис. 5



Рис.

6

Направляющие косинусы (рис. 4, 5, 6) с противоположными знаками соответствуют разным квадрантам, через которые проходит главная нормаль.

Заметим, что база знаний WolframAlpha позволяет находить главные напряжения и направляющие косинусы с помощью операторов eigenvalues и eigenvectors. Запросы для их нахождения имеют, соответственно, следующий вид:

eigenvalues {{50,-20,30},{-20,100,40},{30,40,-100}}

eigenvectors {{50+114.458, -20, 30},{-20, 100+114.458, 40},{30, 40, -100+114.458}}

Результаты решения совпадают с решением в системе Mathcad [1] – рис. 7, 8.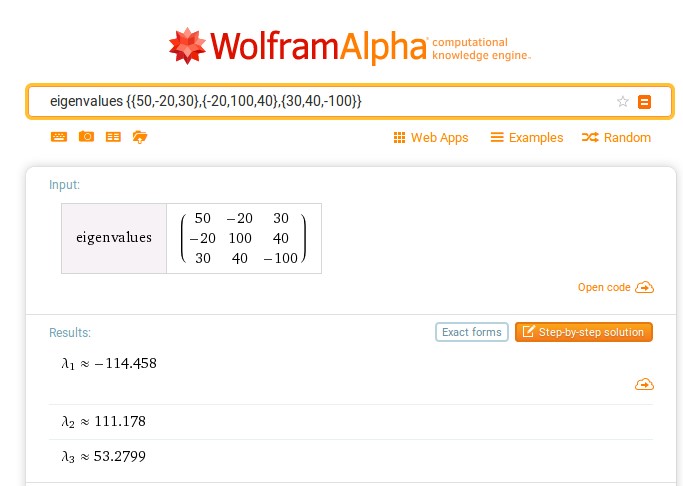



Рис. 7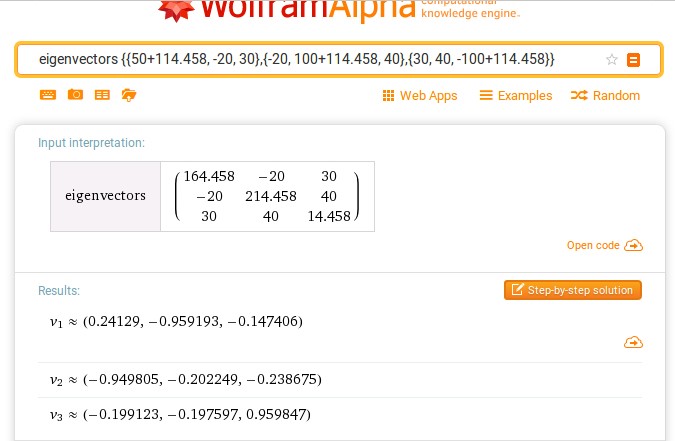



Рис. 8

Таким образом, сравнивая решения, полученные с помощью системы Mathcad и базы знаний WolframAlpha можно сделать вывод об их полном совпадении. Следовательно, можно рекомендовать предложенный подход с использованием базы знаний WolframAlpha в курсе «Сопротивление материалов» к исследованию напряженного состояния в точке упругого тела.

Ссылки на источники:

1. 
   Макаров Е.Г. Сопротивление материалов на базе Mathcad. – СПб.: БХВ – Петербург, 2004. – 512с.: ил.
   
2. 
   WolframAlpha: Computational Knowledge Engine. Режим доступа: http://www.wolframalpha.com/ - [21.03.2017].
   
3. 
   Клоков А.С., Сорокин А.Н. Wolfram Alpha как рабочая среда для студентов, изучающих курс теоретической механики // Электронный научно-методический журнал Омского ГАУ. - 2016. -№4 (7) октябрь - декабрь. - URL http://e-
   

journal.omgau.ru/index.php/2016-god/7/32-statya-2016-4/463-00208. - ISSN 2413-4066

4. 
   Справочник по сопротивлению материалов / Г.С. Писаренко, А.П. Яковлев, В.В. Матвеев; отв. ред. Г.С. Писаренко. – 2-е изд., перераб. и доп. – Киев: Наук. думка, 1988. – 736 с.
   
5. 
   Сопротивление материалов: учебник / Г.С. Варданян, Н.М. Атаров, А.А. Горшков; под ред. Г.С. Варданяна. – М.: ИНФРА-М, 2003. – 480 с.: ил. – (серия «Высшее образование»).
   
6. 
   Белый В.Д. Напряжения и деформации в стержнях и стержневых системах: учебное пособие. – Омск: ОмПИ, 1986. – 103 с.
   

Sergey Popov

Senior Instructor

FSBEI HE Omsk SAU, Omsk

Anatoliy Sorokin

Candidate of Technical Sciences, Associate Professor

FSBEI HE Omsk SAU, Omsk

Aleksandr Klokov

Candidate of Physical and Mathematical Sciences, Associate Professor

FSBEI HE Omsk SAU, Omsk

Studying an Elastic Body Stress State with Wolframalpha Knowledge Base in a Course of

"Strength of Materials"

Abstract: This article considers a problem of studying a stress state in a point of an elastic body. We show effectiveness of applying WolframAlpha knowledge base for a solution to this problem. The technique can be recommended to tutors and students in a course of "Strength of materials".

Keywords: WolframAlpha knowledge base, strength of materials, stress state, main stresses, direction cosines, stress tensor.