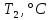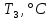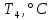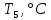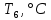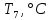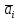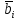ИССЛЕДОВАНИЕ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ В ДИЭЛЕКТРИЧЕСКОЙ СРЕДЕ. Лабораторная работа по физике №11. Исследование нестационарной теплопроводности в диэлектрической среде
 Скачать 116.23 Kb. Скачать 116.23 Kb.
|
|
МИНОБРНАУКИ РОССИИ Санкт-Петербургский государственный электротехнический университет «ЛЭТИ» им. В.И. Ульянова (Ленина) Кафедра физики отчет по лабораторно-практической работе № 11 по дисциплине «Физика» Тема: ИССЛЕДОВАНИЕ НЕСТАЦИОНАРНОЙ ТЕПЛОПРОВОДНОСТИ В ДИЭЛЕКТРИЧЕСКОЙ СРЕДЕ
Санкт-Петербург 2022 Цель работы. Изучение закономерностей процесса тепловой диффузии и определение значения коэффициента тепловой диффузии исследуемого материала. Приборы и принадлежности. Установка для измерения температурного поля, создаваемого в среде тепловым источником. Основные теоретические положения. Уравнение теплопроводности. Теплопроводность характеризует диффузию тепла в среде. Перенос энергии теплового движения в газах осуществляется через столкновения молекул, в твердых телах посредством передачи энергии колебаний кристаллической решетки. В обоих случаях процесс переноса теплоты описывается уравнением диффузии Фика: 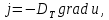 где j – плотность теплового потока; u объемная плотность внутренней энергии среды; 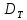 коэффициент тепловой диффузии. Учитывая, что объемная плотность внутренней энергии связана с температурой среды соотношением u = cT, где с теплоемкость единицы объема среды, можно записать уравнение теплопроводности Фурье: коэффициент тепловой диффузии. Учитывая, что объемная плотность внутренней энергии связана с температурой среды соотношением u = cT, где с теплоемкость единицы объема среды, можно записать уравнение теплопроводности Фурье: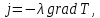 где 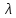 – коэффициент теплопроводности, – коэффициент теплопроводности, 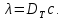 Температурное поле точечного источника тепла. Рассмотрим задачу определения температурного поля T(x; t) в однородной среде. Положим, что температурное поле создается импульсным точечным источником тепла. Рассмотрим распространение тепла вдоль однородного бесконечного стержня, расположенного вдоль оси x. Начало координат совместим с положением нагревателя, который расположен перпендикулярно оси. Пусть в тонком поперечном слое при x = 0 и t = 0 мгновенно выделилось количество теплоты 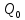 . Выделившееся тепло диффундирует вдоль оси x. Распределение тепла вдоль стержня в любой момент времени соответствует нормальному закону Гаусса: . Выделившееся тепло диффундирует вдоль оси x. Распределение тепла вдоль стержня в любой момент времени соответствует нормальному закону Гаусса: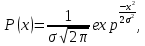 где P(x) – вероятность того, что к некоторому моменту времени порция теплоты будет иметь координату x; 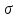 – среднеквадратичная ширина распределения. Тогда распределение линейной плотности тепла вдоль стержня равно: – среднеквадратичная ширина распределения. Тогда распределение линейной плотности тепла вдоль стержня равно: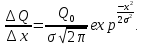 Разделим обе части этого равенства на произведение (сS), где с теплоемкость единицы объема стержня, S площадь его поперечного сечения: 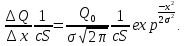 Левая часть данного выражения есть приращение температуры относительно исходной. Она равна приращению температуры T(x; t) в точке с координатой x в момент времени t по отношению к температуре в момент времени t = 0: T(x; t) = T(x; t) - T(x; 0). Тогда искомое распределение температуры вдоль стержня имеет вид 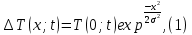 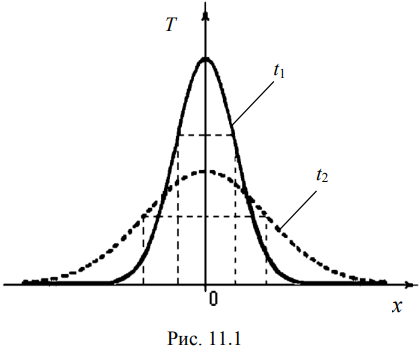 где где 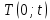 – температура стержня к моменту времени tв точке среды с координатой x= 0; – температура стержня к моменту времени tв точке среды с координатой x= 0; 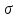 – среднеквадратичная ширина распределения температуры по координате x. Кривые распределения температуры по координате для двух моментов времени показаны на рис. 11.1. – среднеквадратичная ширина распределения температуры по координате x. Кривые распределения температуры по координате для двух моментов времени показаны на рис. 11.1.С увеличением времени параметр увеличивается, при этом температура T(0; t), соответствующая максимуму распределения, уменьшается. Неравновесное состояние неравномерно нагретого стержня релаксирует к равновесному состоянию с одинаковой температурой во всех точках стержня. Зависимость от времени можно представить в следующем виде: 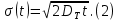 Формула (2) аналогична соотношению Смолуховского – Эйнштейна для среднеквадратичного смещения частицы, совершающей броуновские блуждания. Задача работы – сверить выводы теории теплопроводности в диэлектриках с экспериментом и определить значение коэффициента тепловой диффузии для исследуемого материала. Для этой цели зависимость (1), используя операцию логарифмирования, можно линеаризовать и привести к виду 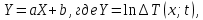 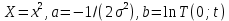 . Коэффициенты a и b в этой линейной зависимости могут быть найдены методом наименьших квадратов (МНК). . Коэффициенты a и b в этой линейной зависимости могут быть найдены методом наименьших квадратов (МНК).Для проверки закона 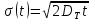 запишем его в виде запишем его в виде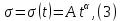 где 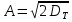 . Эту формулу также можно линеаризовать, используя операцию логарифмирования. В результате придем к зависимости . Эту формулу также можно линеаризовать, используя операцию логарифмирования. В результате придем к зависимости 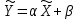 , где , где 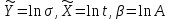 , коэффициенты и в которой также могут быть найдены по МНК. , коэффициенты и в которой также могут быть найдены по МНК.По найденному значению коэффициента 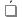 можно найти значение коэффициента можно найти значение коэффициента 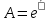 , а затем значение коэффициента тепловой диффузии, , а затем значение коэффициента тепловой диффузии, 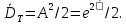 Если полученное значение 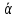 близко к 1/2, то закон близко к 1/2, то закон 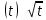 в данном опыте выполняется. Степень отличия в данном опыте выполняется. Степень отличия 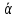 от 1/2 может служить мерой невыполнения теоретических допущений в данном эксперименте. от 1/2 может служить мерой невыполнения теоретических допущений в данном эксперименте.Протокол наблюдений к лабораторной работе №11 «Исследование нестационарной теплопроводности в диэлектрической среде» Таблица 11.1
Таблица 11.2
Выполнил: Дошаков М.М. гр. 2201 Работа выполнена « » декабря 2022 г. Проверил(а) _____________ ________ Контрольные вопросы 19. Как зависит коэффициент диффузии и коэффициент внутреннего трения от средней скорости теплового движения молекул? Коэффициент диффузии: 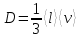 Коэффициент внутреннего трения: 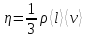 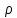 – плотность газа – плотность газа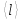 – средняя длина свободного пробега молекул – средняя длина свободного пробега молекул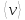 – средняя скорость теплового движения молекул – средняя скорость теплового движения молекулСледовательно, коэффициенты прямо пропорциональны средней скорости теплового движения молекул. 9. Какие явления относятся к явлениям переноса и почему? Явления переноса – это явления, в результате которых происходит перенос либо массы вещества, либо теплоты, либо импульса (количества движения). К явлениям переноса относятся диффузия, теплопроводность и внутреннее трение. Явление диффузии заключается в том, что происходит самопроизвольное проникновение и перемешивание частиц двух соприкасающихся газов, жидкостей и твердых тел. Диффузия сводится к обмену масс частиц этих тел. Перенос массы вещества подчиняется закону Фика: 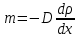 Явление теплопроводности заключается в передаче энергии от более нагретого тела к менее нагретому. Процесс передачи энергии в форме теплоты подчиняется закону теплопроводности Фурье: 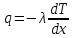 Внутреннее трение – это явление возникновения силы трения между слоями газа (или жидкости), перемещающимися параллельно друг другу с разными по величине скоростями. Внутреннее трение подчиняется закону Ньютона: 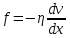 1. Явления переноса – это явления, в результате которых происходит перенос либо массы вещества, либо теплоты, либо импульса (количества движения). Перенос массы вещества подчиняется закону Фика: 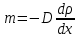 , где , гдеD – коэффициент тепловой диффузии Процесс передачи энергии в форме теплоты подчиняется закону теплопроводности Фурье: 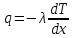 , где , где 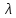 – коэффициент теплопроводности – коэффициент теплопроводностиВнутреннее трение подчиняется закону Ньютона: 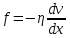 , где , где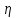 – коэффициент внутреннего трения. – коэффициент внутреннего трения.2. Теплопроводность – это молекулярный перенос теплоты между непосредственно соприкасающимися телами или частицами одного тела с различной температурой, при котором происходит обмен энергией движения структурных частиц (молекул, атомов, свободных электронов). Другими словами, это способность материала проводить тепло. Для количественной оценки теплопроводности существует коэффициент теплопроводности. Чем больше значение коэффициента теплопроводности, тем лучше он проводит тепло. Коэффициент теплопроводности определяется уравнением Фурье и численно равен плотности теплового потока, проходящего через изотермическую поверхность при единичном температурном градиенте: 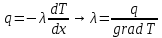 3. Длина свободного пробега молекулы — это среднее расстояние λ, которое пролетает частица за время между двумя последовательными столкновениями. В кинетической теории вводится понятие средней длины свободного пробега 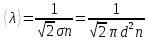 , где , где 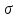 – эффективный диаметр молекулы, – эффективный диаметр молекулы,n – концентрация молекул Обработка результатов 1. Вычислите приращение температуры среды относительно исходной температуры T(x; t) = T(x; t) T(x; 0)
2. Построить графики распределения приращения температуры в координатах (x, T) для каждого значения времени tj 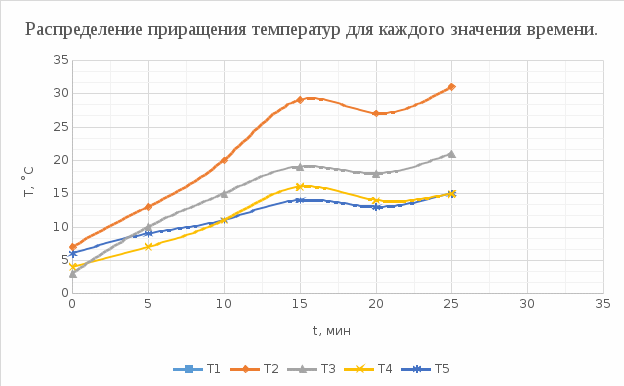 3. 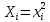 и и 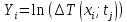 . Найти коэффициенты линейных зависимостей Y1=a1X+b1, Y2=a2X+b2 . Найти коэффициенты линейных зависимостей Y1=a1X+b1, Y2=a2X+b2
4. Построить графики распределения температуры в приведенных координатах (X, Y) для каждого значения времени tj 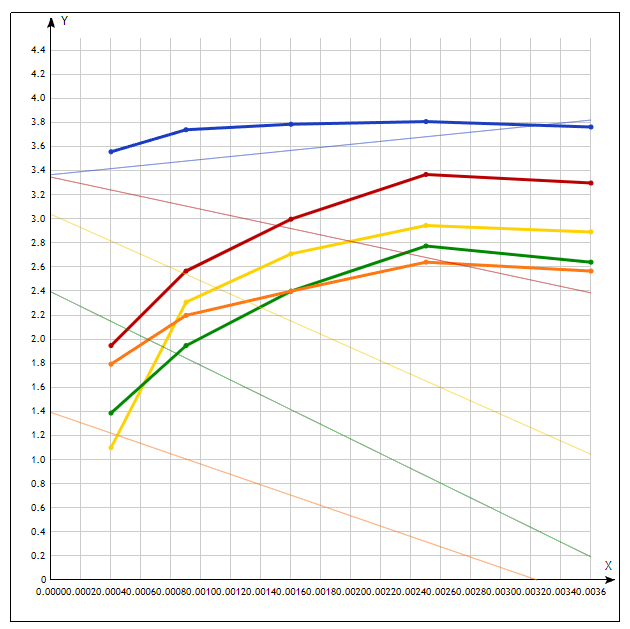 5. Введите обозначения 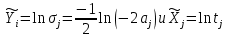 . Используя МНК, найдите по набору . Используя МНК, найдите по набору 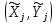 коэффициенты коэффициенты 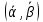 линейной зависимости линейной зависимости 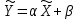
Коэффициенты: 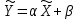 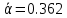 , , 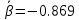 6. Сопоставьте найденное по МНК значение со значением 1/2 Полученное значение 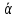 < 1/2 => теоретическая зависимость среднеквадратичной ширины распределения температуры от времени < 1/2 => теоретическая зависимость среднеквадратичной ширины распределения температуры от времени 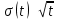 выполняется. выполняется.7. Найти значение коэффициента диффузии 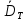 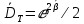 = 0.088 = 0.088Вывод: в ходе работы мной была исследована теплопроводность в диэлектрической среде. Был найден коэффициент диффузии и исследована зависимость среднеквадратичной ширины распределения температуры от времени. | |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||