Статистика шпоры. Исследование обобщенных показателей Задачи статистики Определение размеров явлений

• Название: Исследование обобщенных показателей Задачи статистики Определение размеров явлений
• Анкор: Статистика шпоры.docx
• Дата: 28.01.2017
• Размер: 235.42 Kb.
• Имя файла: Статистика шпоры.docx
• Тип: Исследование; #366
• Категория: Экономика. Финансы
• страница: 3 из 7

2) индекс цен:

где р₁ и р₀ – цена единицы продукции в отчетном и базисном периодах;

3) Изменение объема реализации товара в стоимостном выражении отражает индивидуальный индекс товарооборота:

Индивидуальные индексы по существу – это относительные величины динамики, выполнения плана или сравнения. Индекс выражается в виде коэффициентов и в процентах.

17 вопрос: Агрегатные индексы цен, физического объема, товарооборота, их взаимосвязь.

Агрегатный индекс – представляет собой относительный пок-ль, в числителе и знаменателе которого набор каких-то величин или в числителе и знаменателе сумма произведений 2-х величин, одна из которых индексируемая, а вторая – весовой соизмеритель. Индексируемые величины будут разными, а соизмеритель один и тот же. Рассмотрим агрегатные индексы:

а) агрегатный индекс цен, в качестве соизмерителя берется количество продукции отчетного периода

; q – соизмеритель

б) агрегатный индекс себестоимости продукции, в качестве соизмерителя берется количество продукции отчетного периода

; z – себестоимость, q – количество продукции.

в) агрегатный индекс производительности труда, в качестве соизмерителя берется количество продукции отчетного периода

г) агрегатный индекс количества продукции (индекс физического объема товарооборота), в качестве соизмерителя берется цена или себестоимость базисного периода

; p₀ – цена базисного периода или себестоимости

д) Агрегатный индекс товарооборота фактических цен,  соизмеритель отсутствует

В международной статистике для построения агрегатных индексов применяются следующие обозначения:

q — физический объем произведенной продукции (количество);

p — цена;

z — себестоимость;

d — структура (удельный вес);

1 — отчетный период;

0 — базисный период.

Между индексом цены, индексом физического объема и индексом товарооборота существует взаимосвязь:

Индексы постоянного, переменного состава и индексы структурных сдвигов.

18 вопрос: Средне-арифметические и средне-гармонический индексы цен и физического объема продукции.

Среднеарифметический и среднегармониче-ский индексы.

Агрегатные индексы цен, физического объема товарооборота и другие могут быть рассчитаны, если известны индексируемые величины и веса, т. е. p и q. Допустим, что имеется произведение pq и индивидуальные индексы. Возникает проблема построения средних индексов, идентичных агрегатным, путем осреднения индивидуальных индексов.

Преобразование агрегатного индекса в среднеарифметический можно рассмотреть на примере агрегатного индекса физического объема товарооборота.

В данном случае индивидуальные индексы должны быть взвешены на базисные соизмерители. Из индивидуального индекса физического объема товарооборота i_q= q₁/ q₀ следует, что q₁= i_q/ q₀.

Если заменить q₁ в числителе агрегатного индекса физического объема товарооборота

I_q= Σq₁p₀/ Σq₀p₀, на i_q/q₀,

то получим I_q= Σi_qq₀p₀/ Σq₀p₀.

Это среднеарифметический индекс физического объема товарооборота.

Но если не известны отдельные значения q₁ и p₁, а дано их произведение q₁p₁ – товарооборот отчетного периода и индивидуальные индексы цен i_p= Р₁ / /р₀, и сводный индекс рассчитывается с отчетными весами, то применяется среднегармонический индекс цен. Необходимо, чтобы индивидуальные индексы были взвешены так, чтобы среднегармонический индекс совпал с агрегатным. Из формулы i_p= Р₁ / Р₀ определяем неизвестное значение р₀ и, заменив в формуле агрегатного индекса цен I_p= Σq₁p₁/ Σq0p0 значение Р₀ = Р₁/ i_p, получаем I_p= Σp₁q₁/ Σ(p₁/ i_p)q₁=Σp₁q₁/ Σ(p₁q₁/ i_p)

Этот индекс называется среднегармоническим.

19

20

21

19 вопрос: Индексы постоянного состава, переменного состава и структурных сдвигов, их взаимосвязь.

Индекс переменного состава – индекс, выражающий соотношение средних уровней изучаемого явления, относящихся в разным периодам времени. Например, индекс переменного состава себестоимости продукции: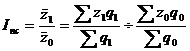

.

Отражает изменение не только изменение индексируемой величины (в данном случае, себестоимости), но и структуры совокупности весов (объем).

Индекс постоянного состава – это индекс, исчисленный с весами, зафиксированными на уровне одного какого-либо периода, и показывающий изменение только индексируемой величины. Например, индекс фиксированного состава себестоимости продукции:



Индекс структурных сдвигов – индекс, характеризующий влияние изменения структуры изучаемого явления на динамику среднего уровня этого явления: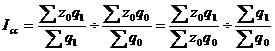



Система взаимосвязанных индексов при анализе динамики средней себестоимости имеет следующий вид:

20 вопрос: Выборочное наблюдение, виды выборки (повторная. бесповторная).

Выборочное наблюдение – это метод статистического исследования, при котором обобщающие показатели совокупности устанавливаются только по отдельно взятой части на основе положений случайного отбора. При выборочном методе изучению подвергается только некоторая часть изучаемой совокупности, при этом подлежащая изучению статистическая совокупность называется генеральной совокупностью. Выборочной совокупностью или просто выборкой можно называть отобранную из генеральной совокупности часть единиц, которая будет подвергаться статистическому исследованию.

Различают четыре вида отбора совокупности единиц наблюдения.

1. Случайный отбор – наиболее распространенный способ отбора в случайной выборке, его еще называют методом жеребьевки, при нем на каждую единицу статистической совокупности заготовляется билет с порядковым номером. Далее в случайном порядке отбирается необходимое количество единиц статистической совокупности. При этих условиях каждая из них имеет одинаковую вероятность попасть в выборку, например тиражи выигрышей, когда из общего количества выпущенных билетов в случайном порядке наугад отбирается определенная часть номеров, на которые приходятся выигрыши. При этом всем номерам обеспечивается равная возможность попасть в выборку.

2. Механический отбор – когда вся совокупность разбивается на однородные по объему группы по случайному признаку, потом из каждой группы берется только одна единица. Все единицы изучаемой статистической совокупности предварительно располагаются в определенном порядке, но в зависимости от объема выборки механически через определенный интервал отбирается необходимое количество единиц.

3. Типический отбор. Исследуемая статистическая совокупность разбивается по существенному, типическому признаку на качественно однородные, однотипные группы, затем из каждой этой группы случайным способом отбирается определенное количество единиц, пропорциональное удельному весу группы во всей совокупности. Типический отбор дает более точные результаты, так как при нем в выборку попадают представители всех типических групп.

4. Серийный (гнездовой) отбор. Отбору подлежат целые группы (серии, гнезда), отобранные случайным или механическим способом. По каждой такой группе, серии проводится сплошное наблюдение, а результаты переносятся на всю совокупность.

Точность выборки зависит и от схемы отбора. Выборка может быть проведена по схеме повторного и бесповторного отбора.

Повторный отбор. Каждая отобранная единица или серия возвращается во всю совокупность и может вновь попасть в выборку. Это так называемая схема возвращенного шара.

Бесповторный отбор. Каждая обследованная единица изымается и не возвращается в совокупность, поэтому она не попадает в повторное обследование. Эта схема получила название невозвращенного шара.

Комбинированный отбор может проходить одну или несколько ступеней. Выборка называется одноступенчатой, если отобранные однажды единицы совокупности подвергаются изучению.

21 вопрос: Средняя и предельная ошибки выборки. Расчет доверительного интервала выборки.

Ошибка выборки — это объективно возникающее расхождение между характеристиками выборки и генеральной совокупности. Она зависит от ряда факторов: степени вариации изучаемого признака, численности выборки, методов отбора единиц в выборочную совокупность, принятого уровня достоверности (значимости) результатов исследования.
Определение ошибки выборочной средней.
При случайном повторном отборе средняя ошибка выборочной средней рассчитывается по формуле:

При бесповторном отборе она рассчитывается по формуле:



Предельная ошибка выборки Δ связана со средней ошибкой выборки μ  отношением: Δ = t*μ. При этом, t - как коэффициент кратности средней ошибки выборки, зависит от значения вероятности Р, с которой гарантируется величина предельной ошибки выборки. Коэффициент доверия позволяет вычислить предельную ошибку выборки. Интервал, в который с данной степенью вероятности будет заключена неизвестная величина оцениваемого параметра, называют доверительным, а вероятность Р – доверительной вероятностью. Чаще всего доверительную вероятность принимают равной 0,95 или 0,99, тогда коэффициент доверия t равен соответственно 1,96 и 2,58. Это означает, что доверительный интервал с заданной вероятностью заключает в себе генеральную среднюю (генеральную долю). Чем больше величина предельной ошибки выборки, тем больше величина доверительного интервала и тем, следовательно, ниже точность оценки.

Коэффициент доверия t и соответствующие уровни доверительной вероятности:

Предельная ошибка выборки при бесповторном отборе определяется по следующим формулам: 1. для доли,  2. для средней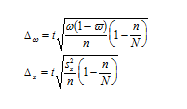

Предельная ошибка выборки при повторном отборе определяется по формуле: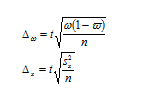

22

23

24

22 вопрос: Расчет необходимой численности выборки, обеспечивающей заданную точность наблюдения.

Одним из научных принципов в теории выборочного метода является обеспечение достаточного числа отобранных единиц. Теоретически необходимость соблюдения этого принципа представлена в доказательствах предельных теорем теории вероятностей, которые позволяют установить, какой объем единиц следует выбрать из генеральной совокупности, чтобы он был достаточным и обеспечивал репрезентативность выборки.

Уменьшение стандартной ошибки выборки, а следовательно, увеличение точности оценки всегда связано с увеличением объема выборки, поэтому уже на стадии организации выборочного наблюдения приходится решать вопрос о том, каков должен быть объем выборочной совокупности, чтобы была обеспечена требуемая точность результатов наблюдений. Расчет необходимого объема выборки строится с помощью формул, выведенных из формул предельных ошибок выборки (Δ), соответствующих тому или иному виду и способу отбора. Так, для случайного повторного объема выборки (n) имеем: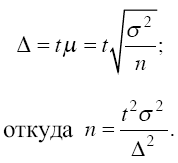



Суть этой формулы – в том, что при случайном повторном отборе необходимой численности объем выборки прямо пропорционален квадрату коэффициента доверия (t²) и дисперсии вариационного признака (σ²) и обратно пропорционален квадрату предельной ошибки выборки (σ²). В частности, с увеличением предельной ошибки в два раза необходимая численность выборки может быть уменьшена в четыре раза. Из трех параметров два (t и σ) задаются исследователем. При этом исследователь исходя из цели

и задач выборочного обследования должен решить вопрос: в каком количественном сочетании лучше включить эти параметры для обеспечения оптимального варианта? В одном случае его может больше устраивать надежность полученных результатов (t), нежели мера точности (σ), в другом – наоборот. Сложнее решить вопрос в отношении величины предельной ошибки выборки, так как этим показателем исследователь на стадии проектировки выборочного наблюдения не располагает, поэтому в практике принято задавать величину предельной ошибки выборки, как правило, в пределах до 10 % предполагаемого среднего уровня признака. К установлению предполагаемого среднего уровня можно подходить по разному: использовать данные подобных ранее проведенных обследований или же воспользоваться данными основы выборки и произвести небольшую пробную выборку. Наиболее сложно установить при проектировании выборочного наблюдения третий параметр в формуле – дисперсию выборочной совокупности. В этом случае необходимо использовать всю информацию, имеющуюся в распоряжении исследователя, полученную в ранее проведенных подобных и пробных обследованиях.

Вопрос об определении необходимой численности выборки усложняется, если выборочное обследование предполагает изучение нескольких признаков единиц отбора. В этом случае средние уровни каждого из признаков и их вариация, как правило, различны, и поэтому решить вопрос о том, дисперсии какого из признаков отдать предпочтение, возможно лишь с учетом цели и задач обследования.

23 вопрос: Ряды динамики: понятие, виды (моментные, интервальные). Приведение рядов к сопоставимому виду.

Процесс развития, движения социально-экономических явлений во времени в статистике принято называть динамикой. Для отображения динамики строят ряды динамики, которые представляют собой ряды изменяющихся во времени значений статистического показателя, расположенного в хронологическом порядке.

В каждом ряду динамики имеются два основных элемента:

1) период времени t (годы, кварталы, месяцы, сутки) или моменты времени;

2) уровни ряда (y).

Уровни рядов динамики отображают количественную оценку (меру) развития во времени изучаемого явления. Они могут выражаться абсолютными, относительными или средними величинами.

Существуют различные виды рядов динамики, которые можно классифицировать следующим образом.

1. По времени -  моментные и интервальные.

Интервальный ряд динамики- это последовательность, в которой уровень явления относится к результату, накопленному или вновь произведенному за определенный интервал времени. (Например, ряд показателей объема продукции по месяцам года).

Если же уровень ряда показывает фактическое наличие изучаемого явления в конкретный момент времени, то совокупность уровней образует моментный ряд динамики(Например, последовательность показателей численности населения на начало года).

Важное аналитическое отличие моментных рядов от интервальных состоит в том, что сумма уровней интервального ряда дает вполне реальный показатель — общий выпуск продукции за год, общие затраты рабочего времени, общий объем продаж и т.д., сумма же уровней моментного ряда реального содержания не имеет.

2. По форме представления уровней-  ряды абсолютных. Относительных и средних величин.

3. По расстоянию между датами или интервалами времени выделяют полные и неполные хронологические ряды.

Полные ряды динамики имеют место, когда даты регистрации или окончания периодов следуют друг за другом с равными интервалами. Неполные —когда принцип равных интервалов не соблюдается.

4. По числу показателей можно выделить изолированные и комплексные (многомерные) ряды динамики.

Если ведется анализ во времени одного показателя, имеем изолированный ряд динамики. Комплексный ряд динамики получаем в том случае, когда в хронологической последовательности дается система показателей, связанных между собой единством процесса или явления.