Статистика шпоры. Исследование обобщенных показателей Задачи статистики Определение размеров явлений
 Скачать 235.42 Kb. Скачать 235.42 Kb.
|
| 10 | 11 | 12 |
| 10 вопрос: Средние величины: понятие, формы, виды. Средняя величина – это обобщающая характеристика единиц совокупности по какому-либо варьирующему признаку. Средние величины позволяют сравнивать уровни одного и того же признака в различных совокупностях и находить причины этих расхождений. В анализе изучаемых явлений роль средних величин огромна. Средняя величина приобретает особую значимость в условиях рыночной экономики. Она помогает определить необходимое и общее, тенденцию закономерности экономического развития непосредственно через единичное и случайное. Виды средних величин:
| 11 вопрос: Средняя арифметическая величина: простая и взвешенная. Основные свойства средней арифметической. Средняя арифметическая является наиболее распространенным видом степенных средних, используется в случаях, когда объём усредняемого признака является аддитивной величиной, т.е. образуется как сумма его значений по всем единицам статистической совокупности. Средняя арифметическая простая используется при работе с несгруппированными данными и рассчитывается по формуле: 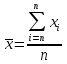 Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднююсгруппированных величин. Если в исходных данных отдельные значения усредняемого признака повторятся, то расчет средней проводится по сгруппированным данным иливариационным рядам. В подобных случаях для расчета необходимо применять среднюю арифметическую взвешенную – среднююсгруппированных величин.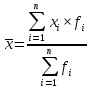 , Где , Где 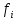 - вес (частота значения признака i единицы совокупности) - вес (частота значения признака i единицы совокупности)Средняя арифметическая обладает рядом полезных свойств, к важнейшим из которых относятся: 1. Средняя арифметическая постоянной величины равна этой величине: 2 . Алгебраическая сумма отклонений вариант от их средней арифметической равно нулю: 3. Если все варианты уменьшить (увеличить) на постоянное число А, то средняя арифметическая из них уменьшится (увеличится) на это же число: 4. Если все варианты одинаково увеличить (уменьшить) в одно и то же число раз, то средняя арифметическая увеличится (уменьшится) во столько же раз: 5. Если все веса средней одинаково увеличить (уменьшить) в несколько раз, то средняя арифметическая не изменится. 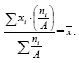 | 12 вопрос: Структурные средние: мода и медиана. Для характеристики структуры статистической совокупности применяются показатели, которые называют структурными средними. К ним относятся мода и медиана. Мода (Мо) – чаще всего встречающийся вариант. Модой называется значение признака, которое соответствует максимальной точке теоретической кривой распределений. Мода представляет наиболее часто встречающееся или типичное значение. Мода применяется в коммерческой практике для изучения покупательского спроса и регистрации цен. В дискретном ряду мода – это варианта с наибольшей частотой. В интервальном вариационном ряду модой считают центральный вариант интервала, который имеет наибольшую частоту (частность). В пределах интервала надо найти то значение признака, которое является модой. где x0– нижняя граница модального интервала; h– величина модального интервала; fm– частота модального интервала; fm -1 – частота интервала, предшествующего модальному; fm+ 1 – частота интервала, следующего за модальным. Мода зависит от величины групп, от точного положения границ групп. 31б Мода – число, которое в действительности встречается чаще всего (является величиной определенной), в практике имеет самое широкое применение (наиболее часто встречающийся тип покупателя). Медиана (Me)– это величина, которая делит численность упорядоченного вариационного ряда на две равные части: одна часть имеет значения варьирующего признака меньшие, чем средний вариант, а другая – большие. Медиана – это элемент, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Свойство медианы заключается в том, что сумма абсолютных отклонений значений признака от медианы меньше, чем от любой другой величины. Применение медианы позволяет получить более точные результаты, чем при использовании других форм средних. Порядок нахождения медианы в интервальном вариационном ряду следующий: располагаем индивидуальные значения признака по ранжиру; определяем для данного ранжированного ряда накопленные частоты; по данным о накопленных частотах находим медианный интервал: Медиана делит численность ряда пополам, следовательно, она там, где накопленная частота составляет половину или больше половины всей суммы частот, а предыдущая (накопленная) частота меньше половины численности совокупности. |
| 13 | 14 | 15 |
| 13 вопрос: Статические ряды распределения: назначение, виды. Статистические ряды распределения представляют собой упорядоченное расположение единиц изучаемой совокупности на группы по группировочному признаку. Различают атрибутивные и вариационные ряды распределения. Атрибутивный – это ряд распределения, построенный по качественным признакам. По количественному признаку строится вариационный ряд распределения. Он состоит из частоты (численности) отдельных вариантов или каждой группы вариационного ряда. Данные числа показывают, насколько часто встречаются различные варианты (значения признака) в ряду распределения. Сумма всех частот определяет численность всей совокупности. В зависимости от характера вариации признака различают дискретные и интервальные вариационные ряды распределения. В дискретном вариационном ряде распределения группы составлены по признаку, изменяющемуся дискретно и принимающему только целые значения. В интервальном вариационном ряде распределения группировочный признак, составляющий основание группировки, может принимать в определенном интервале любые значения. Вариационные ряды состоят из двух элементов: частоты и варианты. Вариантой называют отдельное значение варьируемого признака, которое он принимает в ряду распределения. Частота – это численность отдельных вариант или каждой группы вариационного ряда. Если частоты выражены в долях единицы или в процентах к итогу, то их называют частотами. Виды рядов:
Частость – относительная частота представляется долями (удельными весами) абсолютной численности единиц в общей совокупности. Накопленная частота – это численность единиц образующиеся от группы к группе путем суммирования предыдущих частот. | 14 вопрос: Показатели вариации: абсолютные и относительные. Вариация – различие в значениях какого-либо признака у разных единиц данной совокупности в один и тот же период или момент времени. К показателям вариации относятся: I группа - абсолютные показатели вариации
II группа - относительные показатели вариации
| 15 вопрос: Правило сложения дисперсий, коэффициент детерминации. Согласно правилу сложения дисперсий, общая дисперсия равна сумме средней из внутригрупповых и межгрупповой дисперсий. Пользуясь правилом сложения дисперсий, можно всегда по двум известным дисперсиям определить третью – неизвестную. Чем больше доля межгрупповой дисперсии в общей дисперсии, тем сильнее влияние группировочного признака на изучаемый признак. Поэтому в статистическом анализе широко используется эмпирический коэффициент детерминации - показатель, представляющий собой долю межгрупповой дисперсии в общей дисперсии результативного признака и характеризующий силу влияния группировочного признака на образование общей вариации: 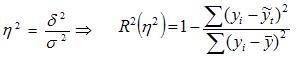 При отсутствии связи эмпирический коэффициент детерминации равен нулю, а при функциональной связи – единице. Общая дисперсия D(x) измеряет вариацию признака по всей совокупности под влиянием всех факторов, обусловивших эту вариацию. Она равна среднему квадрату отклонений отдельных значений признака (хi) от общей средней величины и может быть вычислена как: 1. простая дисперсия 2. взвешенная дисперсия Межгрупповая дисперсия (факторная) характеризует систематическую вариацию результативного признака, обусловленную влиянием признака-фактора, положенного в основание группировки. Она равна среднему квадрату отклонений групповых (частных) средних от общей средней: Внутригрупповая дисперсия (частная, остаточная, случайная) отражает случайную вариацию неучтенных факторов и не зависящую от признака-фактора, положенного в основание группировки. |
| 16 | 17 | 18 |
| 16 вопрос: Индексы: понятие, виды. Индивидуальные индексы цен, физического объема, товарооборота. Индекс – это относительная величина, показывающая во сколько раз уровень изучаемого явления в данных условиях, отличается от уровня того же явления в других условиях. Статистический индекс — это относительная величина сравнения сложных совокупностей и отдельных их единиц. При этом под сложной понимается такая статистическая совокупность, отдельные элементы которой непосредственно не подлежат суммированию. Виды индексов различают по следующим факторам:
Для удобства восприятия индексов в теории статистики разработана символика: - q – количество единиц какого-либо вида продукции; - p – цена единицы какого-либо вида продукции; - z – себестоимость единицы какого-либо вида продукции; - t – трудоемкость единицы какого-либо вида продукции Индивидуальные индексы Показатели, характеризующие изменение более или менее однородных объектов, входящих в состав сложного явления, называются индивидуальными индексами – ix. 1) индекс физического объема продукции: где q1 и q0 – количество произведенной продукции в отчетном и базисном периодах. Данный индекс характеризует изменение физического объема продукции во времени, в пространстве, если сравнивать производство одного и того же вида продукции за один и тот же период времени, но по разным объектам (заводам, территориям и т. д.), и плана, если фактический выпуск сравнивать с плановым заданием; |

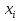 - индивидуальное значение признака i единицы совокупности.
- индивидуальное значение признака i единицы совокупности.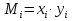
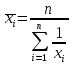
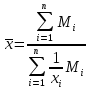
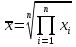
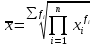
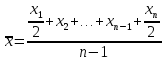
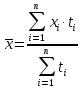 , где
, где