Исследование по линейному приближению б) исследование с помощью функций Ляпунова в) определение устойчивости по фазовому портрету в окрестности особой точки (если не работают теоремы о первом приближении)
 Скачать 178.27 Kb. Скачать 178.27 Kb.
|
|
Задание. 1. Постройте фазовый портрет системы: а) найдите область существования и единственности решений; б) нарисуйте изоклины 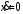 и и 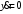 , разбивающие фазовое пространство системы на области, где , разбивающие фазовое пространство системы на области, где  и и 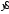 сохраняют знаки. В полученных областях определите знаки сохраняют знаки. В полученных областях определите знаки  и и 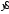 (и направление векторного поля); (и направление векторного поля); в) найдите точки покоя, для каждой точки напишите систему линейного приближения и определите тип особой точки; г) нарисуйте глобальный фазовый портрет системы; д) выделите множество траекторий, отвечающих ограниченным при 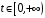 решениям. решениям.2. Нарисуйте фазовый портрет системы при различных значениях параметра  . При каких значениях параметра существуют ограниченные при . При каких значениях параметра существуют ограниченные при 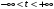 решения данной системы? Устойчивы ли эти решения? решения данной системы? Устойчивы ли эти решения?3. Исследуйте на устойчивость по Ляпунову решение задачи Коши. Докажите по определению устойчивость или асимптотическую устойчивость или неустойчивость этого решения. 4. Исследуйте на устойчивость указанное периодическое решение данной системы. 5. Исследуйте на устойчивость нулевое решение системы (в зависимости от параметров). (Считаем, что 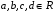 , , 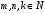 .) .)Предполагается, что вы продемонстрируете знание всех основных приемов: а) исследование по линейному приближению; б) исследование с помощью функций Ляпунова; в) определение устойчивости по фазовому портрету в окрестности особой точки (если не работают теоремы о первом приближении). Вариант 1. 1. 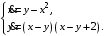 2. 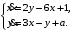 3. 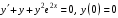 . .4. 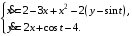 Решение Решение 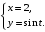 5. 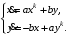 Вариант 2. 1. 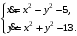 2. 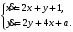 3. 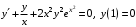 . .4. 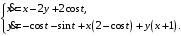 Решение Решение 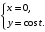 5. 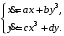 Вариант 3. 1. 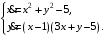 2. 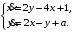 3. 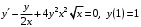 . .4. 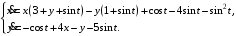 Решение Решение 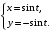 5. 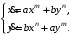 Вариант 4. 1. 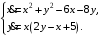 2. 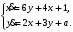 3. 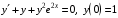 . .4. 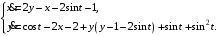 Решение Решение 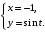 5. 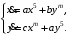 Вариант 5. 1. 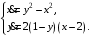 2. 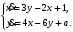 3. 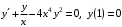 . .4. 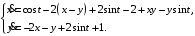 Решение Решение 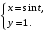 5. 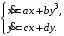 Вариант 6. 1. 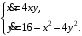 2. 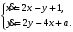 3. 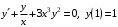 . .4. 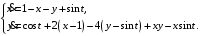 Решение Решение 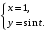 5. 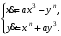 Вариант 7. 1. 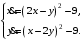 2. 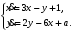 3. 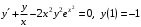 . .4. 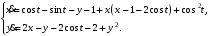 Решение Решение 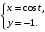 5. 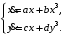 Вариант 8. 1. 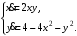 2. 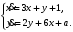 3. 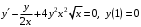 . .4. 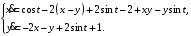 Решение Решение 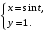 5.  Вариант 9. 1. 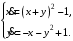 2. 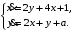 3. 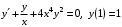 . .4. 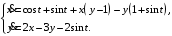 Решение Решение 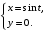 5. 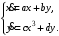 Вариант 10. 1. 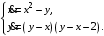 2. 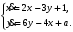 3. 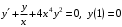 . .4. 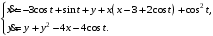 Решение Решение 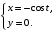 5. 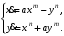 Вариант 11. 1. 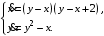 2. 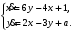 3. 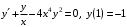 4. 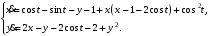 Решение Решение 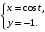 5. 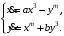 Вариант 12. 1. 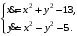 2. 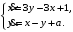 3. 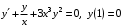 . .4. 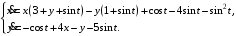 Решение Решение 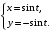 5.  Вариант 13. 1. 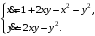 2. 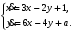 3. 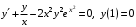 . .4. 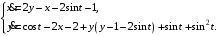 Решение Решение 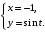 5. 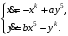 Вариант 14. 1. 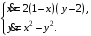 2. 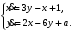 3. 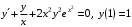 . .4. 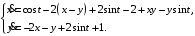 Решение Решение 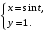 5. 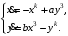 |
