Главная страница
Навигация по странице:

  • Требуется

    		•

    Теория телетрафика. Вариант 9. Исследование процесса поступления сообщений на системы коммутации


    Скачать 199.86 Kb.
    НазваниеИсследование процесса поступления сообщений на системы коммутации
    Дата16.06.2020
    Размер199.86 Kb.
    Формат файлаdocx
    Имя файлаТеория телетрафика. Вариант 9.docx
    ТипИсследование
    #130485
    страница1 из 3
      1   2   3

    Задача 1. Исследование процесса поступления сообщений на системы коммутации

    Условие: На телефонной станции организовано наблюдение за процессом поступления сообщений. Весь период наблюдения (25 ч), на протяжении которого поток является практически стационарным, разделен на n=100 интервалов длительностью t=15 мин. Для каждого интервала определяется число поступающих сообщений. Данные наблюдений группируются в статистический ряд по m членов, характеризующихся числом интервалов nk (k = 1, 2, …, m) с одинаковым числом вызовов ck в интервале

    Таблица 1. Исходные данные.

    № п/п
    ck
    nk

    1
    0
    0

    2
    1
    0

    3
    2
    1

    4
    3
    3

    5
    4
    6

    6
    5
    9

    7
    6
    12

    8
    7
    14

    9
    8
    14

    10
    9
    13

    11
    10
    10

    12
    11
    7

    13
    12
    5

    14
    13
    3

    15
    14
    3






    100


    Требуется: Оценить следующие характеристики процесса поступления сообщений.

    1. Рассчитать эмпирические вероятности   распределения числа вызовов на интервале длительностью t = 15 мин.

    2. Рассчитать среднее статистическое значение числа вызовов   в интервале t=15 мин.

    3. Рассчитать вероятности распределения Пуассона Pk на интервале t=15 мин.

    4. Рассчитать число степеней свободы r и меру расхождения 2 между теоретической вероятностью Pk и эмпирической 

    5. Определить соответствие эмпирического распределения числа сообщений в интервале t=15 мин распределению Пуассона

    Решение

    Эмпирические вероятности распределения числа вызовов рассчитываются по формуле



    Таблица 2. Эмпирические вероятности распределения числа вызовов

    № п/п
    ck
    nk


    1
    0
    0
    0

    2
    1
    0
    0

    3
    2
    1
    0,01

    4
    3
    3
    0,03

    5
    4
    6
    0,06

    6
    5
    9
    0,09

    7
    6
    12
    0,12

    8
    7
    14
    0,14

    9
    8
    14
    0,14

    10
    9
    13
    0,13

    11
    10
    10
    0,1

    12
    11
    7
    0,07

    13
    12
    5
    0,05

    14
    13
    3
    0,03

    15
    14
    3
    0,03






    100
    1

    Среднее статистическое значение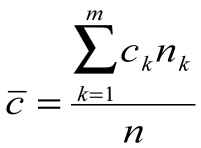

    , где n – число интервалов наблюдения.

    = 7,97

    Значения вероятностей распределения Пуассона могут быть определены по справочным таблицам или рассчитаны по формуле



    Таблица 3. Значения вероятностей распределения Пуассона

    k
    ck
    Pk(t)

    1
    0
    0

    2
    1
    0,1839397206

    3
    2
    0,1804470443

    4
    3
    0,1680313557

    5
    4
    0,1562934519

    6
    5
    0,1462228081

    7
    6
    0,137676978

    8
    7
    0,1303774322

    9
    8
    0,1240769173

    10
    9
    0,118580076

    11
    10
    0,1137363961

    12
    11
    0,1094298885

    13
    12
    0,1055703835

    14
    13
    0

    15
    14
    0
      1   2   3

    написать администратору сайта