Бонч ИНО Теория телетрафика. Теория телетрафика. Вариант 9. Исследование процесса поступления сообщений на системы коммутации
 Скачать 179.05 Kb. Скачать 179.05 Kb.
|
|
Для математической модели М/М/v: Вероятность задержки вызова P{γ>0} = ср=0,21 Вероятность ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях tдоп равна Для 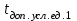 Р=0,08987 Р=0,08987Для 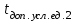 Р=0,04037 Р=0,04037Для 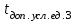 Р=0,008152 Р=0,008152Вероятность ожидания P1{γ>t} свыше допустимого времени t для задержанного вызова при фиксированных значениях tдоп равна P1{γ>t}=  Для 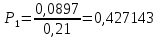 Для 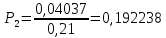 Для 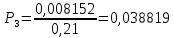 Среднее время ожидания для любого поступившего вызова: 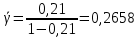 с сСреднее время ожидания для задержанного вызова: 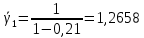 с сСреднее число ожидающих вызовов равно 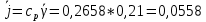 Эрл ЭрлНа основании полученных результатов построим график 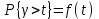 и график и график 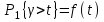 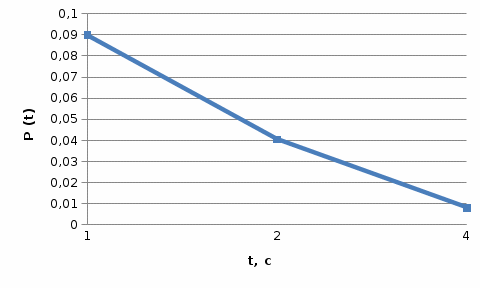 Рисунок 1 - График функции 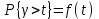 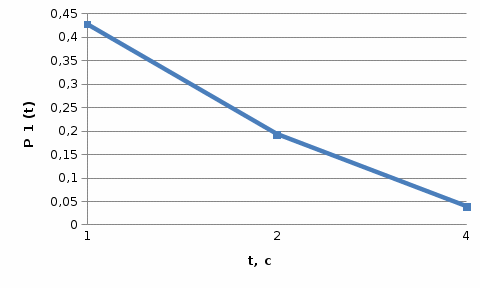 Рисунок 2 - График функции 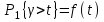 Для математической модели М/D/v: Вероятность задержки вызова P{γ>0} = ср=0,21 Для нахождения вероятности ожидания P{γ>t} свыше допустимого времени t для любого поступающего вызова при фиксированных значениях tдоп воспользуемся кривыми Кроммелина Для Для Для Для  Для 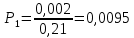 Для 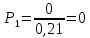 Среднее время ожидания для любого поступившего вызова: 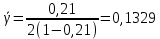 с сСреднее время ожидания для задержанного вызова: 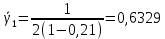 с сНа основании полученных результатов построим график 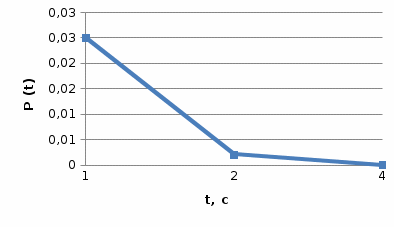 Рисунок 3 - График функции 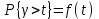 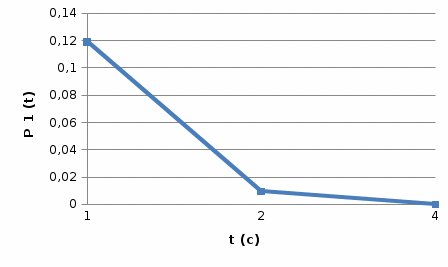 Рисунок 4 - График функции Вывод При увеличении 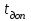 в обоих случаях вероятности ожидания обслуживания свыше допустимого времени для любого поступающего и задержанного вызовов снижаются, но в случае с показательным распределением длительности обслуживания вероятность снижается плавно на всей временной оси, а при постоянной длительности занятия сначала резко уменьшается, а потом плавно и медленно уменьшается. в обоих случаях вероятности ожидания обслуживания свыше допустимого времени для любого поступающего и задержанного вызовов снижаются, но в случае с показательным распределением длительности обслуживания вероятность снижается плавно на всей временной оси, а при постоянной длительности занятия сначала резко уменьшается, а потом плавно и медленно уменьшается.С ростом ср среднее время ожидания для любого поступившего и для любого задержанного вызова начинает расти. Чем больше ср, там дольше вызовам приходится ожидать обслуживания. |
